Метод сравнения продаж (метод прямого сравнения)

Метод сравнения продаж (метод прямого сравнения)

Метод сравнения продаж – один из методов сравнительного подхода, основан на сравнении объекта оценки с аналогичными объектами, в отношении которых имеется информация о ценах сделок с ними.

Метод сравнения продаж предполагает корректировку рыночных цен аналогов на выявленные различия по отдельным элементам. Поправки вносятся в цену аналога исходя из того, сколько бы стоил аналог, имея такие же характеристики, что и объект оценки.

(5)

В общем случае рыночную стоимость машины или единицы оборудования определяют по формуле:

— цена объекта-аналога на момент продажи;

  — коэффициент приведения цены аналога к моменту оценки;

 — коэффициент, учитывающий уторговывание цены предложения аналога

 — коэффициент физического износа (обесценения) аналога за период эксплуатации с момента выпуска до момента оценки;

— коэффициент физического износа (обесценения) объекта оценки за период эксплуатации с момента выпуска до момента оценки;

К1, К2,... Кт — корректирующие параметрические коэффициенты, учитывающие отличия в значениях технических параметров у оцениваемого объекта и аналога;

Цдоп — цена дополнительных устройств, наличием которых отличаются сравниваемые объекты. Эта цена берется на момент оценки.

Коэффициент приведения цены аналога к моменту оценки  показывает, во сколько раз изменились цены на подобные машины за период с момента продажи аналога до момента оценки. Этот коэффициент представляет собой отношение индекса цен на момент оценки к индексу цен на момент действия цены для рассматриваемой группы оборудования.

Коэффициент физического износа (обесценения) аналога за период эксплуатации с момента выпуска до момента оценки. Износ может определяться разными способами: либо как отношение периода эксплуатации до момента продажи к нормативному сроку службы, либо как произведение темпа снижения рыночной стоимости подержанного оборудования на единицу наработки или ресурса на объем наработки или ресурс за период эксплуатации.

(6)

Корректирующие параметрические коэффициенты рассчитываются по следующей формуле:

Ki = (Xi/Xaнi) ^ Ai,

Xi, Хан i — значения i-го параметра у оцениваемого объекта и аналога;

Ai — показатель степени, характеризующий силу связи цены объекта от i-го параметра.

 

Чем больше Ai, тем больше крутизна зависимости цены от параметра. В частном случае при Ai = 1 получаем пропорциональную связь Ki = Xi/Хан i. Внесение корректирующих параметрических коэффициентов дает удовлетворительные результаты, если технические параметры у оцени­ваемого и аналогичного объекта различаются не более, чем на 20%.

С помощью корректирующих коэффициентов могут быть учтены различия между сравниваемыми объектами по таким качественным характеристикам, как дизайн, эргономика, экология, комфортность управления и т. п. В этом случае эксперты оценивают качественные характеристики в баллах по соответствующим шкалам и балльные оценки включаются в формулу для расчета Ki.

Метод расчета по корреляционным моделям

Регрессионный и корреляционный анализ позволяет установить и оценить зависимость изучаемой случайной величины y от одной или нескольких других величин x, и делать прогнозы значений y. Параметр y, значение которого нужно предсказать, является зависимой переменной или показателем-фактором. Параметр xi, значения которого нам известны заранее и который влияет на значения y, называется независимой переменной.

Уравнение регрессии показывает, как в среднем изменяется y при изменении любого из xi имеет вид:

(7)

где y – зависимая переменная (она всегда одна);

   X₁, X₂…X _n – независимые переменные

Если независимая переменная одна – это простой регрессионный ана­лиз. Если же их несколько (n ≥ 2), то такой анализ называется многофак­торным.

Количество факто­ров, включаемых в модель, ограничивается объемом наблюдений (число факторов должно быть, по крайней мере, втрое меньше числа наблюдений).

Множественная линейная регрессия выражается линейной функцией (прямой) и имеет следующий вид:

(8)

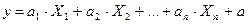
где y – функция регрессии;

X₁, X₂…X _n – независимые переменные

 a₁, a₂…a_n – коэффициенты регрессии;

a  – свободный член уравнения;

n – число факторов, включаемых в модель

 

Независимые переменные являются, по сути, частными показателями, влияющими в своей совокупности на сводные (синтетические) показатели.

Множественная нелинейная регрессия, выражается нелинейной функцией (гиперболой, экспонентой и параболой).

В ходе регрессионного анализа решаются следующие основные задачи:

1. Устанавливается форма зависимости между показателями (линейная или нелинейная, простая или множественная);
2. Определяется функция регрессии в виде математического уравнения того или иного типа и устанавливается влияние главных существенных факторов на зависимую переменную;
3. Оцениваются неизвестные значения зависимой переменной. При этом следует помнить, что расчет дает лишь среднюю оценку зависимой переменной и ее ис­тинное значение может отличаться от расчетного. Это отличие тем существеннее, чем сильнее влияние случайных и не учтенных в модели факторов и чем слабее связь между переменными модели.

Метод корреляционно-регрессионного анализа использован при расчете эмпирического коэффициента Δ T, учитывающего влияние на износ объекта движимого имущества его возраста.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: