Будущая и приведенная стоимости дивидендов и пены акций «Танис» (руб.)

Годы	Будущая стоимость	Приведенная стой мость
D1	P1			P0
	12,1 13,31 14,64 23,58 61,16 1 067,19 125 278,29	133,10 146,41 161,05 259,37 672,75 11 739,09 137 8061,23	8,33 15,97 22,98 29,39 35,28 58,11 82,45 98,71 99,98	91,67 84,03 77,02 70,61 64,72 41,89 17,55 1,29 0,02

Кроме того, многие инвесторы планируют свои действия на огра­ниченный период времени. Портфель ценных бумаг инвестора посто­янно обновляется — для достижения своих целей инвестору необхо­димо продавать одни ценные бумаги и покупать другие. Таким образом, более реалистичной является ситуация, когда инвестор по­купает акции, а через, какое-то время их продает. В этом случае расчет цены акции осуществляется по формуле (5.10).

Задача инвестора состоит в том, чтобы как можно точнее спрогно­зировать величину ожидаемых дивидендов и изменение будущей цены акции. Наиболее простой способ решения проблемы заключается в том, что мы предполагаем постоянные темпы роста цены и дивиден­дов.

Если компания стремится поддерживать постоянный темп роста дивидендов, то можно записать следующее:

D₂ = D₁(1 + g),

D₃ = D₂(1 + g) = D₁ (1 + g)²,

D_i = D₁ (1 + g)^{i – 1}, (5.13)

где D_l, D₂,..., D_i — дивиденды первого, второго,..., i-го года;

g — темп прироста дивидендов.

Подставляя в формулу (5.10) соответствующие значения D₁, полу­чаем:

. (5.14)

Мы видим, что выражение (5.14) за исключением последнего сла­гаемого представляет собой сумму первых n членов геометрической прогрессии, поэтому после несложных преобразований получаем:

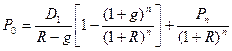. (5.15)

При неограниченном возрастании числа п (п → ∞) последнее сла­гаемое в формуле (5.14) стремится к нулю, а оставшаяся часть пред­ставляет собой сумму членов бесконечно убывающей геометрической прогрессии, которая может быть определена по формуле (5.2). Про­изведя соответствующие преобразования, получаем:

. (5.16)

Заметим, что формула (5.16) справедлива при g = const и R > g.

Пример 5.6.

На фондовом рынке продаются акции акционерного общества «Ориент». Ожидаемые дивиденды в следующем году — 5 руб. на ак­цию, а ожидаемая цена акции — 55 руб. Прогнозируемые темпы при­роста дивидендов и курсовой цены - 10 % в год. Требуемая норма прибыли на акцию — 20 % годовых. Определить цену акции, если ин­вестор собирается держать акцию: а) 3 года; б) неограниченное вре­мя.

Решение:

а) используя формулу (5.15), получаем:

руб.

б) используя формулу (5.16), получаем:

руб.

Как видим, применение формул (5.15) и (5.16) приводит к одним и тем же результатам. Иначе и быть не может, так как цена акций должна быть одинакова независимо от того, на какой срок приобре­тает ее инвестор — на короткое или длительное время.

На основании формулы (5.16) нетрудно заключить, что при требу­емой норме прибыли и ожидаемом уровне дивидендов первого года цена акции будет зависеть от темпа прироста дивидендов. Задача ин­вестора состоит, следовательно, в том, чтобы правильно определить темп прироста дивидендов.

Для прогнозирования темпа прироста дивидендов можно исполь­зовать данные о выплате дивидендов за прошлые годы. Например, из­вестно, что дивиденды на акцию компании «Фарма» составляли:

1999 г. - 2,2 руб., 2000 г. - 2,4 руб., 2001 г. - 2,5 руб.,

2002 г. - 3 руб., 2003 г. - 3,1 руб., 2004 г. - 3,6 руб.

Если предположить, что темп прироста дивидендов является в этом периоде постоянным, то, как было показано ранее, дивиденд любого года можно определить через дивиденд базисного года по формуле (5.13):

D_n = D₁ (1 + g)^n–1,

После преобразования получаем:

,

,

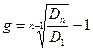. (5.17)

В нашем примереD₁ = 2,2 руб.; D₆ = 3,6 руб., значит:

или 10,35%.

Ожидаемые темпы прироста дивидендов можно спрогнозировать также на основе использования данных бухгалтерской отчетности ис­следуемой компании.

Следует заметить, что полученные результаты расчетов ни в коем случае нельзя абсолютизировать. Их можно рассматривать только в качестве ориентира для инвестора. Дело в том, что определить ожи­даемый размер прибыли, дивидендов, темпов роста дивидендов мож­но лишь с некоторой степенью вероятности. В то же время даже не­большая погрешность в прогнозах может привести к ошибочным действиям инвестора и к серьезным потерям. В конечном счете, ры­ночная цена акций будет определяться соотношением спроса и пред­ложения, поведением на фондовом рынке крупных участников, ко­торые в разные периоды времени могут вести игру на повышение или понижение курса определенного вида ценных бумаг.

Доходность акции

Доходность за период владения акцией, если она находилась у ин­вестора менее года, может быть определена по формуле:

, (5.18)

где R — доходность акции из расчета годовых;

Р_b — цена покупки акции;

Р_s — цена продажи акции;

D — дивиденды, полученные за период владения акций;

Т — период владения акцией (в днях).

Пример 5.7.

Акция приобретена инвестором 1 февраля за 40 руб., продана 1 де­кабря того же года за 48 руб. Дивиденды в размере 3 руб. на акцию были выплачены 15 апреля. Определить доходность за период владе­ния акцией.

С учетом того, что акция находилась у инвестора в течение 303 дней (365 -31 -31), имеем:

или 36,14 % годовых.

Однако если акция находилась у инвестора в течение нескольких лет, то данная формула дает искаженные результаты, так как здесь не учиты­вается стоимость денег во времени. Поэтому необходим другой подход.

Пример 5.8.

Инвестор приобрел акцию за 50 руб. и продал ее через 4 года за 84 руб. За время владения акцией инвестор получил дивиденды за пер­вый год 3 руб., за второй год — 4 руб., за третий год — 4 руб. и за четвертый год — 5 руб. Определить доходность от операции с акцией.

Если не учитывать доходов от реинвестирования дивидендов, то после продажи акции инвестор имел на руках сумму 100 руб. (3 + 4 + 4 + 5 + 84). Таким образом, доходность за период владения акцией может быть определена по формуле:

, (5.19)

где R — доходность акции;

P_s — цена продажи акции;

D — дивиденды за период владения акцией;

Р_b— цена покупки акции. Используя эту формулу, получаем:

или 18,92 % годовых.

Однако полученный результат является не совсем точным, так как не учитывает реинвестирование. Для получения более точной оценки воспользуемся методом последовательных приближений, применяя формулу, аналогичную формуле, используемой для определения цены облигаций:

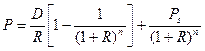, (5.20)

где D — среднегодовой дивиденд;

P_s — цена продажи акции;

R— искомая норма прибыли;

Р — цена покупки акции.

Суть метода заключается в том, что мы будем придавать R различ­ные значения, пока не получим необходимую величину Р.

Предположим, что R = 0,19. В таком случае получаем:

руб.

Поскольку полученное значение цены выше заданного значения (50 руб.), то увеличим значения доходности R до 0,205:

руб.

Полученный результат дает основание заключить, что доходность за период владения акцией составила около 20,5 % годовых.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: