Материалы для самостоятельной работы

Дайте определение следующим ключевым понятиям:облигация, докумен­тарная облигация, бездокументарная облигация, именная облигация, об­лигация на предъявителя, купонная облигация, бескупонная облигация, облигация с плавающей процентной ставкой, инфляционно-индексируемая облигация, валютно-индексируемая облигация, государственная облигация, муниципальная облигация, корпоративная облигация, международная об­лигация, еврооблигация.

Вопросы и задания для обсуждения

1.Какое определение дается облигации в нормативных актах РФ?

2. Как реализуется право старшинства облигаций перед акциями?

3. Может ли выплата заимствованной суммы по облигации выплачи­ваться в неденежной форме?

4. В чем различие купонных и бескупонных облигаций?

5. В каких случаях осуществляется выпуск облигаций с плавающей про­центной ставкой, валютно-индексируемых и инфляционно-индексируемых облигаций?

6. С какой целью осуществляется выпуск государственных облигаций?

7. Может ли государство осуществлять выпуск нерыночных облигаций?

8. Покажите, как осуществляется выпуск государственных краткосроч­ных облигаций в РФ.

9. Дайте характеристику выпускам облигаций федерального займа РФ.

10. В чем различие обеспеченных и необеспеченных корпоративных облигаций?

11. В чем различие между отзывными облигациями и облигациями с
офертами?

12. Как происходит погашение корпоративного облигационного займа?

13. Какие виды облигаций предоставляют их владельцам дополнитель­ные права?

14. Назовите разновидности международных облигаций.

15. Кто является эмитентом еврооблигаций?

16. Приведите примеры выпуска еврооблигаций российскими эмитен­тами.

Литература

Закон «О государственном внутреннем долге РФ» от 13 ноября 1992 № 3877-1.

Федеральный закон РФ «Об акционерных обществах» от 26 декабря 1995 г. №208- ФЗ.

Федеральный закон РФ «О рынке ценных бумаг» от 22 апреля 1996 г. no 39-ФЗ.

Федеральный закон РФ «Об особенностях эмиссии и обращения государ­ственных и муниципальных ценных бумаг от 29 июля 1998 г. № 136-ФЗ.

Федеральный закон РФ «Об ипотечных ценных бумагах» от 11 ноября 2003 г. №152-ФЗ.

Гитман Л. Дж., Джонк М. Д. Основы инвестирования / Пер. с англ. М.: Дело, 1997.

Игнатов И., ФилимошинП. Эмиссия ценных бумаг: Практика и норматив­ные документы. М.: ИЦ «Акционер», 2000.

Литвиненко Л. Т., Штатов Н П., Удалищев Д.П. Рынок государственных бу­маг: Учеб. пособие. М.: Банки и биржи, ЮНИТИ, 1998.

Лялин В.А., Воробьев П.В. Ценные бумаги и фондовая биржа: Учеб. пособие. СПб.: ИД «Бизнес-пресса», 2002;

Лялин С.В. Корпоративные облигации: мировой опыт и российские перспек­тивы. М.: ООО «ДЭКС-ПРЕСС», 2002.

Тихонов Р.Ю., Тихонов Ю.Р. Фондовый рынок. Минск: Амалфея, 2002.

Тъюлз Р., Брэдли Э., Тъюлз Т, Фондовый рынок/ Пер. с англ. М.: ИНФРА-М, 1997.

Фельдман АЛ. Государственные ценные бумаги: Учеб, и справ, пособие. М.: ИНФРА-М, 1995.

Хахонова Н.Н. Валютные облигации. Учет и налогообложение. М.: ПРОИР, 1998.

Шарп У., Александер Г., ЮэйлиДж. Инвестиции / Пер, с англ. М.: ИНФРА-М, 1997.

Глава 7. ЦЕНА И ДОХОДНОСТЬ ОБЛИГАЦИЙ

После изучения этой главы вы сможете получить представление;

· о логике определения стоимости ценной бумаги;

· об особенностях определения цены различных видов облигаций;

· о переменной ставке дисконтирования;

· о процентном доходе продавца и покупателя облигации;

· о доходности облигаций к погашению;

· о доходности облигаций за период владения;

· о реализованном проценте.

Цена облигаций

Облигация имеет номинал (или номинальную цену), эмиссионную цену, цену погашения, курсовую цену и расчетную цену.

Номинальная цена — эта та величина в денежных единицах, кото­рая обозначена на облигации. Как правило, облигации выпускаются с достаточно высоким номиналом. Например, в США чаще всего вы­пускаются облигации с номиналом 1 000 долл.

Эмиссионная цена облигации — это та цена, по которой происходит продажа облигаций их первым владельцам. Эмиссионная цена может быть равна, меньше или больше номинала. Это зависит от типа обли­гаций и условий эмиссии.

Цена погашения — это та цена, которая выплачивается владельцам облигаций по окончании срока займа. В большинстве выпусков цена погашения равна номинальной цене, однако она может и отличаться от номинала.

Курсовая цена — это цена, по которой облигации продаются на вто­ричном рынке. Если каждая облигация имеет строго определенную номинальную цену, цену погашения и эмиссионную цену, уровень ко­торых зафиксирован при выпуске займа, то курсовая цена претерпе­вает значительные изменения в течение срока жизни облигации — она колеблется вокруг теоретической (или внутренней, или расчетной) стоимости (или цены) облигации.

Общий подход к определению теоретической стоимости любой ценной бумаги заключается в следующем: чтобы определить, сколько должна стоить ценная бумага в данный момент времени, необходимо найти приведенную стоимость всех доходов, которые получит инвес­тор за время владения ценной бумагой. Приведенная (текущая) сто­имость денег определяется по формуле:

, (7.1)

где FV — будущая стоимость денег (future value);

PV — настоящая или текущая стоимость денег (present value);

R —- ставка дисконтирования (discount rate);

N — число лет.

Рассмотрим, какова специфика применения этого общего подхо­да к определению стоимости конкретных видов облигаций.

В зависимости от способа выплаты процентного дохода можно вы­делить два типа облигаций: а) облигации с периодической выплатой процентного дохода или купонные облигации; б) бескупонные (или дисконтные) облигации, доход по которым образуется за счет разни­цы между ценой погашения облигации и эмиссионной ценой и вып­лачивается при погашении облигации.

Рассмотрим сначала облигацию с периодической выплатой про­центного дохода.

Пример 7.1.

Продается облигация номиналом 1 000 руб. Процентная (купон­ная) ставка составляет 15 % годовых. Выплата процентов произво­дится 1 раз в год. До погашения облигации остается ровно 5 лет. Тре­буемая норма прибыли (доходность) на инвестиции с учетом риска, соответствующего данному типу облигаций, составляет 20 %. Опре­делить расчетную курсовую цену облигации.

Решение

В конце каждого года держатель облигации получит процентный до­ход в размере 150 руб., а в конце 5-го года — еще и сумму, равную но­миналу облигации, т.е. 1 000 руб. Определим дисконтированные (при­веденные) стоимости доходов дяя каждого года и найдем их сумму.

Приведенная стоимость платежей составит (см. формулу 7.1):

1-й год (руб.);

2-й год (руб.)

3-йгод (руб.)

4-й год (руб.)

5-й год (руб.)

Таким образа, искомая цена облигации будет равна:

125 + 104,17 + 86,80 + 72,34 + 462,16 = 850,47 (руб.).

Часто цену облигации выражают в процентном отношении к ее номиналу. Пришительно к приведенному примеру цена облигации составляет 85,056 от номинала.

Формула для определения стоимости облигации может быть пред­ставлена в виде:

или

, (7.2)

где Р — цена облигации;

D — процентный (купонный) доход в денежных единицах;

R — требуема норма прибыли (ставка дисконтирования).

Если обозначить: 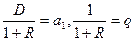, тогда выражение (7.2) примет вид:

(7.3)

Сумма: а₁ + a₁q + a₁q ²+... + a₁q ^n-1 представляет собой сумму пер­вых п членов геометрической прогрессии и может быть определена по формуле:

. (7.4)

 

Подставляя в эту формулу и , имеем:

. (7.5)

После преобразований получаем:

. (7.6)

Следовательно, формула для определения стоимости облигации принимает вид:

. (7.7)

Для приведенного выше примера 7.1 цена облигации, вычислен­ная по формуле (7.7), составит:

(руб.)

Мы получили тот же результат, что и ранее.

Заметим, что приведенные выше расчеты справедливы, если став­ка дисконтирования (требуемая норма прибыли) остается неизмен­ной в течение рассматриваемого периода (срока действия облигации). В действительности ставка может изменяться.

В этом случае для определения приведенной стоимости облигаций требуется найти продисконтированные потоки доходов для каждого года, используя следующую формулу:

, (7.8)

где D_pi — приведенная стоимость дохода i-го года;

d_i — доход i-го года;

R₁, R₂, …, R_i — ставка дисконтирования для 1-го, 2-го,..., i-го года.

Пример 7.2.

По облигации номиналом 1 000 руб. выплачивается 15 % годовых. Выплата процентов производится 1 раз в год. До погашения облига­ции остается 5 лет. Требуемая норма прибыли в течение первых 3 лет — 20 %, 4-й год — 15 %, 5-й год — 10 %. Определить курсовую цену облигации.

Решение

Процентный доход каждого года и сумму погашения облигации необходимо продисконтировать по переменной ставке дисконтиро­вания. Определим дисконтированные стоимости для платежей каж­дого года:

1-й год (руб.);

2-й год (руб.)

3-йгод (руб.)

4-йгод (руб.)

5-йгод (руб.)

Следовательно, цена облигации составит:

Р= 125 +104,17 +-86,80 + 75,48 + 526,09 = 917,54 (руб.).

Мы видим, что стоимость облигации выше, чем в примере 7.1, так как ставка дисконтирования в 4-м и 5-м годах ниже, чем в первые 3 года.

Процентный доход по облигациям может выплачиваться не один, а несколько раз в год, тогда формулы (7.2) и (7.7) будут иметь следую­щий вид:

(7.9)

 

или

, (7.10)

где т — число выплат процентного дохода в течение года.

Пример 7.3.

Номинал облигации 1 000 руб. Процентная ставка 15 % годовых. Выплата процентов производится 2 раза в год. До погашения облига­ции остается 5 лет. Определить курсовую цену облигации, если требу­емая норма прибыли составляет 20 % годовых.

Решение

Если мы сравним стоимость облигации со стоимостью, получен­ной в примере 1, то увидим, что в случае выплаты дохода 2 раза в год при одной и той же норме дисконтирования, стоимость облигации ниже, чем при выплате дохода 1 раз в год.

До сих пор мы рассматривали случаи, когда до погашения облига­ции остается целое число лет или купонных периодов. Однако обли­гации продаются и покупаются в любой момент времени (в начале, середине и в конце купонного периода). Допустим, облигация, о ко­торой шла речь в примере 1, продается не за 5 лет до погашения, а за 4 года и 300 дней. до срока погашения. Покупатель получит годовой процентный доход по этой облигации (при условии выплаты процен­тов 1 раз в год) через 300 дней после покупки облигации. Между тем, в течение 65 дней облигация находилась в руках продавца, которому по праву принадлежит процентный доход за этот период, в то время как покупателю причитается доход только за 300 дней. Процентный доход покупателя и продавца за время Т определяется по формуле:

, (7.11)

где D — процентный доход за год или купонный период;

Т— время, в течение которого облигация находилась в руках про­давца или покупателя (в днях);

D_T — процентный доход за время Т.

В нашем примере процентный доход покупателя составит:

(руб.)

Процентный доход продавца будет равен:

(руб.)

Поскольку процентный доход в размере 26,71 руб., принадлежа­щий продавцу получит покупатель облигации при оплате очередного купона, то цена облигации должна быть увеличена таким образом, чтобы продавец не понес ущерба, В рассматриваемом нами случае цена (цена, вычисленная в примере 7. 1) должна быть увеличена на 26,71 руб. и составить 877,18 руб. (850,47 + 26,71).

Однако это лишь приблизительный результат, так как цена в раз­мере 850,47 руб. была получена нами при дисконтировании доходов ровно за 5 лет. Поэтому, чтобы получить более точный результат, нуж­но продисконтиррвать ожидаемые доходы за тот период времени, ко­торый остается до погашения облигации с момента совершения сделки. Для нецелого числа лет формула приведенной стоимости имеет следующий вид:

, (7.12)

где ;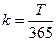

n — целое число лет, включая нецелый год;

Т — число дней до выплаты первого купона.

Определим цену облигации для нашего примера:

(руб.)

Выше речь шла об облигациях с постоянным купоном; Однако ку­понные облигации могут быть как с постоянной, так и переменной купонной ставкой. Последние характеризуются тем, что величина про­центного дохода изменяется в зависимости от изменения ситуации на финансовом рынке. Примерами таких облигаций являются обли­гации федерального займа с переменным купоном (ОФЗ-ПК) и об­лигации государственного сберегательного займа (ОГСЗ). Стоимость таких облигаций определяется по формуле:

, (7.13)

где D₁, D₂,..., D_n – процентный доход i-го периода (I = 1, 2,..., n);

R₁, R₂,..., R_n — требуемая норма прибыли (ставка дисконтирова­ния) i-го периода.

Задача заключается в том, чтобы оценить величину процентных выплат и требуемую норму прибыли в разные периоды.

Пример 7.4.

Номинал облигации 1 000 руб. До погашения остается 3 года. Про­центный доход выплачивается 2 раза в год. По первому купону вып­лачивается 20 % годовых. Определить курсовую цену облигации.

Изучая ситуацию на финансовом рынке, инвестор пришел к вы­воду, что купонная ставка по облигации будет снижаться: 1-й год — 20 % годовых, 2-й год — 18 %, 3-й год — 15 %. Будет снижаться и требуемая норма прибыли по данному типу облигаций: 1-й год — 20 %, 2-й год — 19 %, 3-й год — 16 %. Исходя из этих условий, имеем:

Бескупонную облигацию можно представить как купонную облига­цию с нулевым размером купонных платежей. Поскольку процент­ные платежи при этом равны нулю, то формулы (7.2) и (7.7) прини­мают следующий вид:

(7.14)

Пример 7.5.

Бескупонная облигация номиналом 1 000 руб. погашается по но­миналу через 4 года. Определить курсовую цену облигации, если ставка дисконтирования составляет 14 % годовых.

(руб.)

Если данная облигация погашается через 3 года 180 дней, то ее курсовая стоимость составит:

(руб.)

Формула (7.14) может быть использована и при определении кур­совой стоимости краткосрочных ценных бумаг (со сроком действия менее 1 года) — ГКО, депозитных и сберегательных сертификатов.

Пример 7.6.

Определить цену краткосрочной облигации номиналом 1 000 руб., погашение через 180 дней. Требуемая норма прибыли по данному типу облигаций составляет 20 % годовых.

Используя формулу (7.14), имеем:

(руб.)

Однако для определения цены краткосрочных облигаций обычно используется другая формула:

. (7.15)

Применяя эту формулу, получаем:

(руб.).

Чтобы установить величину различий результатов вычислений при использовании формул (7.14) и (7.15), рассмотрим несколько приме­ров.

Пример 7.7.

Номинал облигации 1 000 руб. Требуемая норма прибыли — 10 % годовых, погашение через 180 дней.

Цена облигации, вычисленная по формуле (7.14):

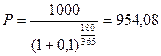(руб.)

по формуле (7.15):

(руб.).

Пример 7.8.

Номинал облигации 1 000 руб. Требуемая норма прибыли 20 % годовых, погашение облигации через 300 дней

Цена облигации при использовании формулы (7.14):

(руб.)

По формуле (7.15) имеем:

(руб.).

Пример7.9.

Номинал облигации 1000 руб. Требуемая норма прибыли 15 % го­довых, погашение облигации через 365 дней.

Цена облигации, рассчитанная по формуле (7.14):

(руб.);

по формуле (7.15):

(руб.).

Приведенные выше примеры показывают следующее:

1. Расхождение в оценке курсовой стоимости облигации при ис­пользовании разных формул тем меньше, чем ниже ставка дисконти­рования. Так, для полугодовой облигации при ставке дисконтирова­ния 20 % расхождение составляет около 0,4% цены, а при ставке дисконтирования 10 % —около 0,1 % цены.

2. При одной и той же ставке дисконтирования расхождение в цене тем меньше, чем больше срок до погашения облигации.

3. При сроке до погашения равном 1 году (365 дней) обе формулы дают один и тот же результат расчетной цены облигации.

Поскольку величины расхождений расчетной цены, полученной с использованием разных формул, являются весьма незначительными, то при вычислениях с краткосрочными инструментами обычно ис­пользуется формула (7.15).

Доходность облигаций

Облигации приобретаются инвесторами с целью получения дохо­да. Процентный (или купонный) доход измеряется в денежных еди­ницах. Чтобы иметь возможность сравнивать выгодность вложений в разные виды облигаций (и других ценных бумаг), следует сопоставить величину получаемого дохода с величиной инвестиций (ценой при­обретения ценной бумаги).

Текущая доходность

Если известна курсовая цена облигации и величина процентного дохода, то можно определить так называемую текущую доходность об­лигации по формуле:

, (7.16)

где R_T — текущая доходность;

D — процентный доход в денежных единицах;

Р — цена облигации.

Пример 7.10.

Облигация номиналом 1 000 руб. продается по цене 800 руб., про­центный доход в размере 30 % годовых выплачивается 1 раз в год. Текущая доходность будет равна:

или 37,5% годовых.

Доходность к погашению

Если инвестор собирается держать облигацию до погашения, то он может сопоставить все полученные по облигации доходы (процен­тные платежи и сумму погашения) с ценой приобретения облигации. Полученная таким способом величина называется доходностью к по­гашению или внутренней нормой прибыли.

Если известная цена облигации, то доходность к погашению мож­но определить методом последовательных приближений, используя формулы (7.2) или (7.7).

При этом в указанные формулы следует подставлять различные зна­чения R и для каждого значения R определять соответствующее зна­чение цены. Если для выбранного значения R, мы получаем цену выше заданного значения цены (Р), то следует увеличить значение R и най­ти новое значение Р. Если получено значение Р ниже заданной цены, то необходимо уменьшить значение R. Такие действия необходимо продолжать до тех пор, пока расчетная цена не совпадет с заданной ценой. Полученное таким образом значение R и будет являться до­ходностью облигации к погашению или внутренней нормой прибыли облигации.

Пример 7.11.

Номинал облигации 1 000 руб. Срок погашения облигации через 5 лет. По облигации выплачивается 20 % годовых, выплата произво­дится 1 раз в. год. Курсовая цена облигации — 930 руб. Определить доходность облигации к погашению.

Предположим, что ставка дисконтирования составляет 22 %. Тог­да, используя формулу (7.7), получаем:

 

(руб.).

Мы получим цену, которая выше курсовой цены облигации. Сле­довательно, норма прибыли (ставка дисконтирования) должна быть увеличена. Увеличим ставку дисконтирования до 23 % и найдем но­вое значение цены облигации:

(руб.).

Мы получили значение цены, которые ниже курсовой цены обли­гации. Следовательно, чтобы получить значение цены, равное курсо­вой стоимости облигации, ставка дисконтирования должна быть ниже 23 %. Искомое значение находится между 22 % и 23 %.

Перенесем полученные результаты на график. По горизонтальной оси отложим значения доходности, а по вертикальной оси — цену об­лигации (рис. 7.1).

 

 

Рис. 7.1. График доходности и цены облигации

 

Соединим полученные точки цены облигации при доходности 22 % и 23 % и найдем точку пересечения этой прямой с горизонтальной прямой, соответствующей цене облигации (930 руб.). Эта точка, как следует из графика, соответствует величине доходности примерно 22,5%.

Однако графическое решение не обеспечивает точных результатов, поэтому проверим найденную величину, а именно: найдем значения цены облигации при ставке дисконтирования, равной 22,5 %.

(руб.).

При ставке дисконтирования, равной 22,5 % цена облигации не­сколько ниже курсовой цены, следовательно, ставка дисконтирова­ния должна быть несколько уменьшена. Определим цену облигации при ставке дисконтирования, равной 22,47 %.

(руб.).

Таким образом, полученное расчетное значение цены (929,97 руб.) фактически совпадает с курсовой ценой облигаций (930 руб.). Зна­чит, данная облигация обеспечивает доходность к погашению в раз­мере 22,47 % годовых.

Доходность к погашению — это ставка дисконтирования, при ко­торой приведенная стоимость процентных платежей и суммы пога­шения облигации равна покупной цене облигации (затратам инвес­тора). На основе вычисленной доходности к погашению можно решать вопрос о приемлемости тех или иных инвестиций. Если инвестор оп­ределил для себя требуемую норму прибыли для данного вида вложе­ний (с учетом риска), и если полученная норма прибыли по облига­ции равна или выше требуемой нормы, то покупка облигаций является выгодным вложением средств. Если же доходность по облигации ниже требуемой нормы прибыли, то такое вложение средств (покупка об­лигаций) является неприемлемым. Так, если в приведенном выше при­мере инвестор считает, что требуемая норма прибыли для данного типа облигации составляет 22 %, то покупка облигации по цене 930 руб. будет являться выгодным вложением средств, так как эти инвестиции обеспечивают доходность в размере 22,47 % годовых.

На графике, построенном по результатам вычислений, видно, что приемлемой ценой для данных облигаций будет даже цена в 942,73 руб., которая обеспечивает уровень доходности в размере 22 % годовых.

Если цена на облигацию поднимется выше 942,73 руб., то от по­купки облигации следует отказаться.

На практике на выбор инвестора оказывают влияние многие фак­торы, поэтому для принятия того или иного решения не всегда необходимо производить точные вычисления. Иногда достаточно иметь лишь приблизительные результаты. Так, чтобы определить приблизи­тельно уровень доходности облигации, можно использовать следую­щую формулу:

, (7.17)

где N — номинал облигации;

Р— цена облигации;

n — число лет до погашения облигации;

D— ежегодный процентный доход по облигации в денежных еди­ницах.

Для приведенного выше примера 7.11 имеем:

или 22,18%

Отклонение приблизительного значения доходности (22,18 %) от точного значения (22,47 %) весьма незначительно и находится в пре­делах допустимой ошибки.

Бескупонная облигация

Доходность бескупонной облигации (облигации с нулевым купо­ном) определяется из формулы (7.14):

.

После преобразований получаем:

, ,

. (7.18)

Если инвестору необходимо сравнить доходность по бескупонным облигациям с доходностью купонных облигаций, с выплатой дохода т раз в год, то формула (7.18) принимает вид:

 

. (7.19)

Пример 7.12.

Цена облигации— 600 руб., номинал 1 000 руб. До погашения об­лигации остается 5 лет. Определить доходность к погашению, если до­ход по купонным облигациям выплачивается: а) 1 раз в год; б) 4 раза в год (ежеквартально).

а) или 10,8 %

б) или 10,35%.

Доходность краткосрочных облигаций (сроком действия до 1 года) обычно определяется по формуле:

. (7.20)

где D — величина дисконта (процентного дохода) в денежных единицах;

Р — цена облигации;

Т—число дней до погашения облигации.

Подставляя вместо D = N-P, получаем:

,

, (7.21)

где N-— номинал облигации.

Пример 7. 13.

Облигация номиналом 1 000 руб. продается с дисконтом по цене 930 руб. До погашения облигации остается 50 дней. Определить до­ходность к погашению, если погашение происходит по номиналу.

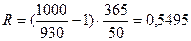или 54,95%

Доходность к погашению облигаций с переменной процентной ставкой (с плавающим купоном) с более или менее достаточной сте­пенью достоверности определить невозможно. Речь может идти толь­ко о весьма приблизительной оценке на основе прогноза развития ры­ночной ситуации. Вместе с тем следует иметь в виду, что величина купонной ставки на очередной купонный период устанавливается, исходя из сложившейся и ожидаемой конъюнктуры рынка на очеред­ной период. По существу облигацию с плавающим купоном (облига­ции типа ОФЗ-ПК или ОГСЗ) можно рассматривать как серию крат­косрочных облигаций, так как доходность таких облигаций на очередной купонный период устанавливается на уровне доходности краткосрочных инструментов. Следовательно, дня таких облигаций це­лесообразно определять доходность к погашению очередного купона, т.е. использовать приведенную выше формулу для определения доход­ности краткосрочных облигаций (7.20).

Пример 7.14.

Облигация номиналом 1 000 руб. продается по цене 1 100 руб. Ве­личина купона — 200 руб. Продолжительность купонного периода — 182 дня. До выплаты купона остается 91 день. Определить доходность облигации.

После выплаты очередного купонного дохода, новый размер купо­на обычно устанавливается таким образом, чтобы цена облигации была близка к номиналу. Следовательно, владелец облигации как бы полу­чает сумму, равную номинальной стоимости облигации (1 000 руб.) и величине купонного дохода (200 руб.), т.е. 1 200 руб. Значит, его доход за период до выплаты купона составляет: D= 1200- 1100- 100руб.

Используя формулу (7.20), получаем:

или 36,46%

Следует отметить, что Центробанк России дал следующую форму­лу для вычисления доходности облигаций ОФЗ и ОГСЗ:

, (7.22)

где N— номинал облигации;

С — величина текущего купона;

Р_ч — чистая цена облигации (цена в самом начале купонного пе­риода);

А — накопленный доход с начала купонного периода;

T— количество дней до конца купонного периода.

Величина А определяется по формуле:

, (7.23)

где t — продолжительность купонного периода.

В нашем примере имеем:

;

или 36,46%.

Мы получили тот же самый результат, так как формула (7.22) яв­ляется модификацией формулы (7.20), Подставляя в формулу (7.20) вместо Р= Р_ч +А; D = Т+С- - (Р_ч + А), получаем:

.

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: