Глава 5 финансовые решения в условиях риска

ДИНАМИЧЕСКИЕ МОДЕЛИ ПЛАНИРОВАНИЯ ФИНАНСОВ

Опишем модели оптимального многоэтапного планирования ин­вестиции в различные проекты. Индекс риска, связанного с реали­зацией каждого из проектов, оценивается экспортно по десятибал­льной шкале. Каждому допустимому проекту отвечает свой задан­ный индекс риска. Общий подход к построению моделей в форме линейного программирования демонстрируется на задачах 5.1 и 5.2.

Задача 5.1. Акционерное общество (АО) закрытого типа зак­лючило контракт на покупку нового оборудования для производ­ства железобетонных блоков стоимостью 750 000 дол. В соот­ветствии с условиями контракта 150 000 дол. в качестве аванса необходимо уплатить через 2 месяца, а остальную сумму - через 6 месяцев, когда оборудование будет установлено. Чтобы рас­платиться полностью и в указанные сроки, руководство АО пла­нирует создать целевой фонд, предназначенный для инвестиций. Поскольку инвестиционная деятельность принесет дополнитель­ную наличность к моменту расчета за приобретенное оборудова­ние, отложить следует не всю сумму в 750 000 дол., а меньшую. Сколько именно, зависит от имеющихся возможностей и правиль­ности организации процесса инвестирования. Акционерное об­щество решило сосредоточиться на 4 направлениях (12 возмож­ностях) использования средств целевого фонда. Данные для за­дачи финансового планирования приведены в табл. 5.1.

Руководство АО ставит перед собой три основные цели:

1) при данных возможностях инвестирования и утвержден­ного графика выплат должна быть разработана стратегия, мини­мизирующая наличную сумму денег, которые АО направляет на оплату оборудования по контракту;

Таблица 5.

Направления использования инвестиций	Возможные начала реализа­ции инвестици­онных проектов, мес.	Длительность инвестицион­ного проекта, мес.	Процент за кредит	Индекс риска
А	1,2,3,4,5,6		1,5
В	1,3,5		3,5
С	1,4		6,0
D

 

2) при разработке оптимальной стратегии средний индекс риска инвестиционных фондов в течение каждого месяца не должен превышать 6. Этот показатель индекса риска, как пред­полагается, отвечает возможностям менеджера фирмы по управ­лению проектами;

3) в начале каждого месяца (после того, как сделаны новые инвестиции) средняя продолжительность погашения инвестици­онных фондов не должна превышать 2,5 месяца. Причины те же, что и в п. 2.

Таким образом, среди потенциально реализуемых проектов выбираются наиболее экономически эффективные, при этом проекты повышенной рисковости должны компенсироваться менее рисковыми, а очень длинные проекты должны выполнять­ся одновременно с более краткосрочными. Для решения данной задачи необходимо, во-первых, подготовить и систематизировать имеющуюся исходную информацию и, во-вторых, построить адекватную сформулированным целям экономико-математичес­кую модель. Динамика возможных вложений и условий возврата денежных средств отражена в табл. 5.2.

Обозначения в модели:

А_i - объем инвестиций в направление (проект) А в начале месяца i (i = 1,2,...,6);

В_i - объем инвестиций в направление (проект) В в начале месяца i (i = 1,3,5);

Таблица 5.2

С_i - объем инвестиции в направление (проект) С в начале месяца i (i = 1,4);

D_i - объем инвестиций в направление (проект) D в начале месяца i (i = 1);

К - объем инвестиций в начале первого месяца.

Цели, на достижение которых направлена инвестиционная деятельность АО, а также необходимые ограничения формализу­ются следующими соотношениями:

1. Начальная сумма инвестиций К должна быть минималь­ной:

К ® min.

2. Согласно табл. 5.2 балансовые ограничения на структуру инвестиций для каждого месяца имеют вид:

3. Ограничения на средневзвешенные риски проектов (для каждого месяца)*:

4. Ограничения на средний срок погашения инвестиционно­го фонда (для каждого месяца):

 

* Запись А В означает, что из истинности условия А вытекает условие В.

 

Таким образом, задача описывается моделью линейного про­граммирования, имеющей 19 ограничений в форме равенств и неравенств и 13 переменных.* Оптимальное решение, найден­ное с помощью специальной компьютерной программы на ПК IBM PC/AT, имеет вид:

 

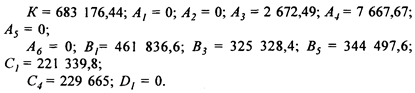
* Последние два ограничения в блоке 4 в силу неотрицательности искомых переменных выполняются всегда, и их можно не учитывать.

 

Благодаря полученному оптимальному решению удалось обеспечить уплату в срок обусловленных контрактом 150 000 дол. и вместо необходимых для конечных расчетов 600 000 дол. (750 000 - 150 000 = 600 000 дол.) заработать К = 683 176,44 дол., часть из которых способствовала уменьшению долговых обя­зательств по контракту (на 13,86 %).

Оптимальное решение показывает, каким неочевидным зара­нее, но эффективным способом распределяются инвестиционные ресурсы по месяцам реализации проекта.

Это демонстрирует возможности линейного программирова­ния, обусловливая эффективность того, что на первый взгляд таковым не казалось.

Задача 5.2. В табл. 5.3 отражены пять проектов, которые конкурируют между собой за получение инвестиционных фон­дов компании. Мы видим, какие наличные деньги будут получе­ны на вложение одного доллара.

Таблица 5.3

Год	Эффективность инвестиционного проекта на один вкладываемый доллар
А	В	С	D	E
Первый	-1,00		-1,00	-1,00
Второй	+0,30	-1,00	+1,00
Третий	+1,00	+0,30			-1,00
Четвертый		+1,00		+1,75	+1,40

 

Например, проект А - это инвестиции, которые можно сде­лать в начале первого года на два следующих года, причем в конце этого же года можно возвратить 30 центов на вложенный доллар, а в конце следующего года можно дополнительно полу­чить еще 1 дол. Максимальная сумма, которая может быть вло­жена в этот проект, составляет 500 000 дол. Проект В полностью аналогичен проекту А, но вложение денег можно сделать только в начале следующего года и т.д. Деньги, полученные в результа­те инвестиций, можно реинвестировать в соответствии с предло­женной схемой. В дополнение к этому компания может получать по 6 % годовых за краткосрочный вклад всех денег, которые не были вложены в инвестиции в данном году.

У компании имеется 1 000 000 дол. для инвестиций. Она хочет максимизировать сумму денег, накопленных к конечному перио­ду. Сформулируем задачу линейного программирования и полу­чим решение на ЭВМ.

Решение. Построим экономико-математическую модель и приведем полученное на ЭВМ оптимальное решение.

Обозначения:

a₁, b₁, c₁, d₁, е₁ - инвестиции в проекты А, В, С, D, Е соот­ветственно; индексы 1,2,3 указывают первый, второй и третий годы вложения инвестиций;

s₁, s₂, s₃ - суммы, которые можно положить под краткосроч­ные 6 % соответственно в первом, втором, третьем годах.

Экономико-математическая модель:

а) в проект А в первый год не может быть вложено более 500 000 дол.:

а₁ £ 500 000;

б) поскольку у компании имеется 1 000 000 дол., то во все проекты эта сумма должна быть вложена в первом году (иначе к конечному периоду компания не максимизирует своих накоп­лений):

a₁, + с₁ + d₁+ s₁ = 1 000 000;

в) аналогичный баланс на второй год:

0,30 a₁ + 1,1 с₁ + 1,06 s₁ = b₁ + s₂;

г) аналогичный баланс на третий год:

а₁ + 0,3 b ₂ + 1,06 s₂ = e₃ + s₃;

д) максимальный доход к конечному периоду:

b₂ + 1,75 d₁ + 1,4 e₃ + 1,06 s₃ ® max.

Полученное оптимальное решение:

Максимальный доход к конечному периоду равен 1 797 600 дол., что указывает на высокую эффективность инвестиционного про­цесса (прирост на 79,76 %). Остальные не приведенные значения указанных переменных модели равны нулю.

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: