Чистая приведенная стоимость (безрисковая ситуация)

Дается ответ на вопрос: сколько вы сегодня заплатите за проект, который через год даст 100 дол. дохода? Плата составля­ет X дол., r - заданный процент прибыли (r % годовых - коэф­фициент дисконтирования):

Рассмотрим безрисковую ситуацию, которая обеспечивает­ся государственными ценными бумагами (облигациями, серти­фикатами и т.д.).

Общее правило: если через t лет мы получим чистые налич­ные в стоимостном выражении NCF, то приведенная к начально­му моменту стоимость проекта PV равна:

Величину PV можно интерпретировать как сумму ожидае­мого дохода минус процент на капитал в качестве компенсации за ожидание.

Исходя из формулы (5.1) выявим некоторые практически важные закономерности.

1. Существует обратная зависимость между величиной PV и продолжительностью периода времени, через которую сумма NCF будет получена: PV для периода t будет больше, чем для периода t + i. Другими словами, сегодняшние деньги дороже завтрашних даже при отсутствии инфляции. А инфляция этот процесс только усиливает.

2. Существует обратная зависимость между величиной РV при определенном размере NCF и коэффициент дисконтировая r: чем больше r, тем значение PV меньше при NCF = const, т.е. чем больше r, тем более сегодняшние деньги дороже завтрашних.

3. Существует прямая зависимость между PV и NCF при фиксированных значениях r и периоде выплаты t.

Пусть в течение периода t мы получаем: через год – NCF₁, через 2 года – NCF₂ ,..., через t лет – NCF_t и пусть r_t – ежегод­ный процент на капитал, который мы получаем через t лет (предполагается, что процент на капитал может ежегодно менять­ся, как это и наблюдается на практике). Тогда приведенная к на­чальному моменту стоимость PV равна:

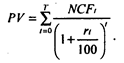
Суть формулы (5.1) при различных значениях г графически отражена на рис.5.1.

Рис. 5.1. Темпы спада pV в зависимости от времени и коэффициента дисконтирования

Пример 5.1. Пусть в конце 1986 г. руководству одной из фирм США предложили участвовать в строительстве и эксплуатации нового офиса в течение 6 лет. Строительство должно начаться 1 января 1987 г. и закончиться 31 декабря 1987 г. Доходы от сдачи здания в аренду и расходы известны с определенностью и пред­ставлены в табл. 5.4 (цифры условные).

Таблица 5.4

Год	Арендные платежи (доход), тыс. дол.	Затраты, тыс. дол.	Чистая прибыль NCF, тыс. дол.

 

Предполагается для простоты, что платежи и поступления имеют место в конце каждого гада. В конце 1992 г. стоимость здания составляла бы 1 млн дол. Какова приведенная стоимость (к началу 1987 г.) проекта в конце 1992 г. - начале 1993 г., если процентные ставки государственных облигации, соответствую­щие одному, двум,..., шести годам, будут такими, как показано в табл. 5.5?

Таблица 5.5

Год выплаты
Процентная ставка (г %)	5,75	6,00	6,25	6,50	6,75	7,00

 

В 1987 г. здание еще строилось и прибыли не давало. Поэто­му NCF₁ = 0.

С учетом данных табл. 5.4 и 5.5 приведенная к начальному моменту (1987 г.) стоимость проекта PV (строительство здания и сдача его в аренду) равна:

Пример 5.2. Рассчитаем чистую приведенную стоимость проекта NPV. Она равна разности между приведенной стоимос­тью всех начальных поступлений от проекта и текущей платой за проект:

NPV = PV - плата за проект. (5.3)

Пусть согласно условиям примера 5.1 фирме предложили 33%-ное участие в шестилетнем соглашении за 450 тыс. дол. Тогда для фирмы

NPV = 0,33*1 393 966 - 450 000 = 10 009 дол. (5.4)

Таким образом, с помощью формул (5.1) - (5.4) отражена экономика одного проекта фирмы. Потенциальные возможности фирмы можно охарактеризовать, по существу, портфелем ее проектов.

Ценность фирмы - это ее чистая приведенная стоимость плюс чистая приведенная стоимость портфеля проектов, т.е. сумма чистых приведенных стоимостей проектов портфеля.

Каким должно быть деловое поведение фирмы, желающей максимизировать свою приведенную стоимость?

Пусть фирма представляется совокупностью п проектов. Станет ли она богаче, приобретя еще один, (n +1)-й, проект? Очевидно, что чистая приведенная стоимость фирмы увеличива­ется, если предельная выгода (приведенная стоимость дополни­тельного проекта) будет больше предельных затрат (того, что мы заплатили за дополнительный проект), т.е. фирма станет богаче, если чистая приведенная стоимость дополнительного проекта положительна.

Фирма может выиграть от сокращения, продав проекты (ка­питал), которые имеют отрицательную чистую приведенную стоимость. То, что невыгодно данной фирме, может быть выгод­но другой, поэтому такие проекты могут купить.

Итак, чтобы максимизировать ценность (стоимость) фирмы в условиях определенности, нужно приобретать капитал (осуще­ствлять проекты) с положительными NPV и избавляться от капи­тала с отрицательным NPV.

Согласно формуле (5.4) предложенный проект имел чистую приведенную стоимость NPV= 10009дол.>0, однако если бы при той же (33 %) доле участия цена за это участие составляла 470 000 дол. (вместо 450 000), то NPV = –9 991 дол. < 0, т.е. такой проект следовало бы отвергнуть.

Таким образом, в условиях определенности относительно малые цифры в разнице (450 000 и 470 000 дол.) затрат за уча­стие в проекте могут решить судьбу проекта с точностью до наоборот.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: