Измерение отношения к риску

Исследуем график функции полезности, представленной на рис. 4.4. Для такого типа ЛПР полезность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с веро­ятностью p выиграть М₁ и с вероятностью (1 - р) выиграть М₂.

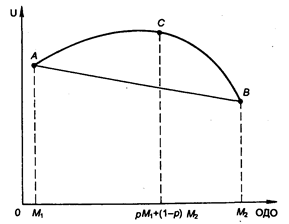
Рис. 4.4. График функции полезности ЛПР, не склонного к риску

 

Формально мы имеем график вогнутой функции, о которой известно, что ордината любой точки кривой больше ординаты точки хорды кривой. Определим соотношение, характеризующее ЛПР, не склонного к риску. Нетрудно видеть, что

U(M₁) - значение полезности в точке А;

U(M₂) - значение полезности в точке В;

U(pM₁ + (1 - р) М₂) - значение полезности в точке С.

Уравнение хорды АВ имеет вид:

U₁ = а + bМ,

где U₁ - совокупность точек, лежащих на отрезке прямой.

Найдем значения параметров а и b уравнения прямой.

В точке А имеем U(M₁) = а + bМ₁.

В точке В имеем U(M₂) = а + bМ₂.

Вычитаем из первого выражения второе, исключая величину a:

U(M₁) – U(M₂) = b(M₁ – М₂),

откуда получаем:

После подстановки значений для параметров а и b уравнение хорды АВ имеет вид:

где М₁ £ М £ M₂.

Пусть М = рМ₁ + (1 – р) М₂, где 0 £ р £ 1, тогда в точке С справедливо неравенство

Подставив в это неравенство вычисленные значения а и b,получим:

или

U (pM₁ + (1 - р)М ₂) > PU(M₁) + (1 - p) U(M ₂). (4.2)

Неравенство (4.2) характерно для функции полезности ЛПР, не склонных к риску. Оно действительно показывает, что полез­ность среднего выигрыша (полезность ОДО) больше ожидаемой полезности игры: с вероятностью р выиграть М₁ и с вероятнос­тью (1 – р) выиграть М₂.

Аналогично можно показать, что для функций полезности ЛПР, склонных к риску, справедливо неравенство

U(pM₁ + (1 – р)М₂) < pU(M₁) + (1 – p)U(M₂). (4.3)

Для функций полезности ЛПР, безразличных (нейтральных) к риску, имеет место равенство

U(pM₁ + (1 – р)М₂) = pU(M₁) + (1 – p)U(M₂). (4.4)

Склонность или несклонность ЛПР к риску, как уже отмеча­лось, зависит от его финансового положения, текущей ситуации принятия решения и других факторов. Иначе говоря, эта харак­теристика ЛПР не является абсолютной, присущей ему при любых обстоятельствах.

Приведем пример игры, по отношению к которой любой игрок не склонен к риску.

Петербургский парадокс (игра придумана петербургскими гусарами). Играют двое. Один бросает монету до тех пор, пока не выпадет «орел». Выигрыш равен (2) ⁿ руб., где п - число брос­ков до появления «орла». Ожидаемая величина выигрыша:

ОДО = 2(1/2) + (2)² (1/4) + (2)³(1/8) +... = 1+1+1+....

Вряд ли какой-либо игрок согласится заплатить за право участвовать в этой игре сумму, равную ОДО: эта сумма беско­нечно велика.

Предположим теперь, что имеет место игра (лотерея) с аль­тернативами a и в, т.е. G(a,в: a). Исследуем проблему, как целе­сообразнее поступить ЛПР: играть или получить гарантирован­ный выигрыш, равный ожидаемому выигрышу. Пусть функция полезности игрока определена как U(W) = ln(W), где W- вели­чина благосостояния. Пусть игра заключается в выигрыше 5 дол. с вероятностью 0,8 и в выигрыше 30 дол. с вероятностью 0,2. Ожидаемая величина выигрыша (ОДО):

E(W) = 5*0,8 + 30*0,2 = 10 дол.

Для указанной логарифмической функции полезности имеем зависимость, выраженную в табл. 4.1.

Таблица 4.1

W
U(W)		1,61	2,30	3,00	3,40

 

Рассчитаем полезность ОДО для данной игры:

U(E(W)) = U (10) = ln(10) = 2,3,

т.е. полезность отказа от игры при получении гарантированного выигрыша, равного 10 дол. (ОДО данной игры), оценивается в 2,3 ютиля (ютиль - условная единица полезности). Если ЛПР предпочтет игру, то

E(U(W)) = 0,8 U (5) + 0,2 U (30) = 0,8*1,61 + 0,2*3,40 = 1,97 ютиля.

Для рассмотренной логарифмической функции полезности большей полезностью обладает вариант с получением гарантированного выигрыша, равного E (W)=ОДО, а не участие в игре (2,3 > 1,97). Такое лицо, принимающее решение, не склонно к риску.

Выводы. Из соотношении (4.2) – (4.4) вытекает:

• если U(E(W)) > E(U(W)), игрок не склонен к риску;

• если U(E(W)) = E(U(W)), игрок нейтрален (безразличен) к риску;

• если U(E(W)) < E(U(W}), игрок склонен к риску.

Здесь Е и U - соответственно символы математического ожидания и функции полезности.

СТРАХОВАНИЕ ОТ РИСКА

Пусть по-прежнему полезность выражается логарифмической зависимостью U(W) = ln (W) (см. табл. 4.1).

Определим, какую максимальную сумму пожелает заплатить ЛПР, чтобы избежать игры, в которой с вероятностью 0,8 он выигрывает 5 дол. (уменьшение выигрыша на 5 дол. по сравне­нию с ОДО = 10 дол.) и с вероятностью 0,2 выигрывает 30 дол. (увеличение выигрыша на 20 дол. по сравнению с ОДО). Значение ожидаемой полезности игры составляет 1,97 ютиля, что соответствует гарантированному выигрышу 7,17 дол. (ln7,17 = 1,97). С другой стороны, сумма ожидаемого выигрыша в случае игры (ОДО) равна 10 дол. Поэтому, чтобы избежать игры, ЛПР согласится заплатить максимальную сумму, равную

10 – 7,17 = 2,83 дол.

Из этого следует, что, если ЛПР предлагают застраховаться от игры и просят за это сумму, меньшую, чем 2,83 дол., ему выгодно принять предложение. В данном случае величина, рав­ная 2,83 дол., - премия (максимальная плата) за риск.

Рассмотрим некоторые приложения теории полезности.

Задача 4.2. Оптимальная величина страхования. Ювелир вла­деет бриллиантом стоимостью 100 000 дол. и желает застраховать его от кражи. Страховка покупается по правилу: цена страховки составляет 20 % от суммы, которую страхуют. Например, если бриллиант страхуется на всю стоимость (100 000 дол.), страховка стоит 20 000 дол., если страхуется на половину цены (50 000 дол.). то страховка обходится в 10 000 дол. Если ювелир будет знать (построит) свою функцию полезности, он сможет рассчитать, на какую оптимальную сумму следует застраховать дорогую вещь.

Ювелир может оказаться в одной из двух ситуации: 1) бриллиант украден; 2) бриллиант не украден. Чем больше сумма страхования, тем больше его состояние (капитал), если бриллиант украден, но тем меньше его состояние, если брил­лиант не украден.

Например, если бриллиант застрахован на 50 000 дол., име­ют место два случая:

1. Бриллиант украден. При этом потери ювелира рассчитыва­ются следующим образом:

-100 000 (бриллиант) - 10 000 (страховка) + 50 000 (компен­сация) = -60 000 дол., а капитал 50 000-10 000 = 40 000 дол.

2. Бриллиант не украден. В этом случае капитал ювелира составит:

100 000 (бриллиант) - 10 000 (страховка) = 90 000 дол.

Если бриллиант застрахован на 100 000 дол., то в случае кражи бриллианта капитал составит 100 000 - 20 000 = 80 000 дол. Если бриллиант не украден, капитал также составит 80 000 дол. Обозначим капитал ювелира в случае, если бриллиант не украден, через Y_n:

Y_n = 100 000 - 0,2К, (4.5)

где К - сумма страхования.

Если бриллиант украден, то капитал ювелира определим как Y_t:

Y_t = 0,8 K.

Соответствующий график, отражающий бюджетное ограни­чение, представлен на рис. 4.5.

Рис. 4.5. Графическое решение задачи 4.2

Предположим, что можно экспертно определить вероятность р того, что бриллиант будет украден. Тогда полезность капитала Y_t, равна U(Y_t). Вероятность того, что бриллиант не украден, со­ставляет (1- р), и U(Y_n) - полезность капитала Y_n в этом случае.

Ожидаемая полезность U «игры» (с вероятностью р брилли­ант украден и с вероятностью (1 - р) - не украден) определяется согласно формуле (4.1) выражением

U = pU(Y_t)+ (1 -p) U (Y_n).

Значения Y_t и Y_n следует выбирать таким образом, чтобы ожидаемая полезность была максимальной, т.е.

pU(Y_t) + (1-р)(Y_n) max.

Пусть точка касания кривой безразличия (линия одинаковой полезности) на рис. 4.5 соответствует Y_n = 86 000 дол., Y_t = 56 000 дол.

Тогда согласно формуле (4.5) имеем: 86 000 = 100 000 - 0,2 К, откуда оптимальная величина страхования К = 70 000 дол.

Задача 4.3. Спрос на страхование. Пусть финансовое состо­яние индивида оценивается заданным значением W. Предполага­ется, что можно вычислить вероятность р потери некоторой ча­сти этого состояния, определяемой суммой L £ W (например, в результате пожара). Индивид может купить страховой полис, в соответствии с которым ему возместят нанесенный ущерб в размере q. Плата за страхование составляет pq, где p - доля страхования в объеме нанесенного ущерба. Проблема состоит в определении значения q.

Исследуем задачу максимизации ожидаемой полезности фи­нансового состояния индивида в ситуации, когда с вероятностью р страховой случай происходит и с вероятностью (1 –р) - не происходит. Тогда задача сводится к поиску максимума по q ожидаемой полезности капитала индивида:

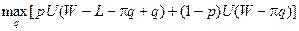
Применим необходимое условие оптимальности - продиффе­ренцируем выражение в квадратных скобках по q и приравняем производную нулю:

где q* - оптимальное значение q. В результате получаем:

Предполагая известным вид функции U, из соотношения (4.6) находим значение q*.

Рассчитаем ожидаемую прибыль страховой компании, учи­тывая, что страховой случай имеет вероятностный характер.

Если страховой случай произошел, компания получает доход pq – q. Если страховой случай не наступил, компания получает доход pq. Поэтому ожидаемая прибыль компании

р(pq - q)+ (1 - р) pq = ppq - pq + pq - ppq = q(p - р),

где р - вероятность наступления страхового случая.

Конкуренция между страховыми компаниями уменьшает прибыль, которая в условиях совершенной конкуренции стремит­ся к нулю, т.е. из условия q(p - р) = 0 следует, что p р.

Это означает, что доля платежа от страхуемой суммы p при­ближается к вероятности несчастного случая р. Если соотноше­ние p = р ввести в условие максимума ожидаемой полезности, то получим:

.

Если потребитель не склонен к риску, то , и из равенства первых производных следует равенство аргументов, т.е.

W – L + (1 - p)q* = W – pq*,

или

– L + q* – pq* = –pq*,

откуда

q* = L.

Вывод. Страховаться целесообразно на сумму, которую мож­но потерять в результате несчастного случая.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: