Свойства статистических игр

Функция решения, отображающая множество выборок X _Q в множество решений статистика A, называется нерандомизирован­ной (чистой) функцией решения статистика. Так, по результа­там эксперимента статистик определяет, какое решение а Î А он должен выбрать. Для выбора из множества D наилучшей функции решения он использует функцию риска.

Функция риска зависит от множества состояний природы и от множества функций решения и принимает значение, выражен­ное действительными числами. Она определяет математическое ожидание функции потерь при некотором состоянии природы Q и известной статистику функции распределения F ( |Q), когда а=d( ).

Представим функцию риска:

,

где M - знак математического ожидания;

L( Q, a) - функция потерь при состоянии природы Q и d( ) = a.

В теории статистических функций любую неотрицательную функцию L, определенную прямым произведением W´ D, назы­вают функцией потерь. Значение L( Q ,d) функции потерь L в про­извольной точке (Q, d) Î W´ D интерпретируют как ущерб, к ко­торому приводит принятие решений d, d Î D, если истинное зна­чение параметра есть Q, Q Î W.

Выражение W´ D - прямое произведение множества состоя­ний природы и множества функций решения. Функция R( Q, d) не является случайной величиной, а принимается как платеж ста­тистика в его игре с природой при следующих условиях:

• состояние природы фиксировано;

• функция решений выбрана, d Î D.

Стратегическая игра (W, A, L) становится статистической, G = (W, D, R), если используется результат эксперимента - век­тор . Игра называется статистической, если в ней:

• X _Q - множество n -мерных выборок;

• D - множество функций решений, которые преобразуют X _Q в А;

• W - множество состояний природы;

• R (Q, d) - функция риска.

Статистическая игра записывается как G = (W, D, R). Данная игра является игрой двух лиц с нулевой суммой, где d Î D -функция решения статистика, а риск R (Q, d) статистика - пла­теж природе.

Статистик может не прибегать к рандомизации, если он ис­пользует как оптимальную байесовскую функцию решения r (см. разд. 6.2.1).

Рандомизация на стороне статистика проводится двумя мето­дами:

1) применение решений а Î А с определенными вероятностя­ми (смешение решений);

2) смешение чистых функций решения d Î D, т.е. рандомиза­ция функций решения.

Чаще применяется второй метод.

Распределение вероятностей d на множестве D чистых фун­кций решения d называется рандомизированной (смешанной) функцией решения статистика.

Функция риска становится случайной величиной, если экс­периментатор применяет в статистической игре случайную фун­кцию решения dÎ D *, т. е. когда каждой чистой функции реше­ния d Î D приписывается вероятность, с которой она должна использоваться.

Платежом будет математическое ожидание функции потерь, взятое для некоторого состояния природы Q при распределении d, определенном на множестве чистых функций решения D:

Если статистик использует случайные функции решения dÎ D *, то этим расширяется (обобщается) статистическая игра.

Расширенная статистическая игра (W, D*, R) называется так­же смешанным расширением статистической игры с рандоми­зацией на стороне статистика.

Дальнейшее расширение статистической игры может быть достигнуто при предположении, что природа также «применяет» стратегию при «выборе» своего состояния Q.

Априорное распределение вероятностей x на множестве Wсостояний природы означает распределение до проведения экспе­римента. Это априорное распределение xÎX состояний природы является случайной (смешанной) стратегией природы в статисти­ческой игре, где природа не рассматривается как разумный игрок.

Если Q предполагается случайной величиной с априорным распределением x, то риск R (Q,d) становится случайной пере­менной при фиксированной функции решения d. В данном слу­чае математическое ожидание риска R (Q,d) при априорном рас­пределении x, задаваемом функцией распределения G( Q ), оп­ределяется как

,

где r (x,d) -байесовский риск функции решения d с учетом априорно­го распределения x.

Если в качестве оптимальной принимается байесовская фун­кция решения, то используется формула r (x,d).

Вводя рандомизацию на стороне природы, приходим к даль­нейшему расширению статистической игры.

Игра (X, D*, r) со смешанным расширением статистической игры с рандомизацией на стороне статистика и на стороне при­роды называется полностью расширенной статистической иг­рой.

Поясним в полностью расширенной статистической игре (X, D*, r) ее составляющие:

X - множество всех априорных распределений x состояний природы или множество ее смешанных стратегий;

D* - множество всех случайных функций решения;

r = r (x,d) - байесовский риск.

Представим схему расширения статистической игры (рис. 6.1). При наличии данных без учета стохастических распределений имеем исходную стратегическую игру двух лиц с нулевой сум­мой, которая относится к антагонистическим играм. Данная игра является исходной для соответствующей статистической задачи принятия решения.

Рис. 6.1. Расширение статистической игры

Если статистик (экспериментатор) не имеет возможности провести эксперимент со случайной величиной X, чтобы полу­чить ее распределение, которое зависит от состояния природы, он вынужден будет использовать только стратегическую игру (W, A, L).

Однако очень часто статистик может провести эксперимент и получить в результате вектор , которым он в состоянии вос­пользоваться при принятии решения аÎА функции d( ). В этом случае платеж L( Q, а) становится случайной величиной, а игра - статистической G(W, D, R). Стратегией статистика будет dÎD, а платежом природе от статистика станет его риск R (Q, d).

Далее у статистика остаются две альтернативы:

1) воспользоваться рандомизацией состояний природы и пе­рейти к расширенной (X, D, r) статистической игре;

2) воспользоваться рандомизацией функций решения и перей­ти к расширенной статистической игре (W, D*, R).

Наконец, если статистик применит смешанные стратегии для обоих игроков, то получит полностью расширенную статисти­ческую игру ((W, D*, r).

На практике статистик для выбора оптимальной стратегии может не производить рандомизацию, а в качестве оптимальной взять байесовскую функцию решения.

А. Вальд, создавая теорию статистических игр, опирался на созданную Д. Нейманом теорию стратегических игр, поэтому сравним далее понятия стратегических игр двух лиц с нулевой суммой и понятия статистических игр статистика с природой. Для этого укажем основные обозначения в стратегической и статистической играх:

Х - совокупности стратегий игрока 1;

Y - совокупности стратегий игрока 2;

W— платежная функция;

W(X,Y) - платеж игрока 2 игроку 1;

G == (X,Y,W) - игра игрока 1 с игроком 2;

Г = (X, Н, К) ~ смешанное расширение игры G = (X, Y,W), где X - множество всех смешанных стратегий x игрока 1;

Н - множество всех смешанных стратегий h игрока 2;

К - риск игрока 2.

Составим сравнительную таблицу задач статистических ре­шений с игрой двух лиц с нулевой суммой (табл. 6.1).

Таблица 6.1

ВЫБОР ФУНКЦИЙ РЕШЕНИЯ

Для всех состояний природы не существует одной наилуч­шей функции решения. От статистика требуется применение таких методов, которые дают оптимальные функции решения в более узком диапазоне.

Для этого необходимо использовать критерии оптимальности.

Статистик в статистической игре (W, D, R) или в расширен­ных статистических играх стремится к выигрышу, т. е. к опреде­лению наилучшей функции решения, при которой риск R (Q, d)был бы минимальным. Но это не просто, так как для каждого состояния природы Q имеется своя лучшая функция.

Пусть у нас имеются две различные функции решения d₁ и (рис. 6.2).

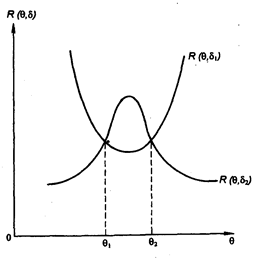
Рис. 6.2. Сравнение двух функций решения

Можно выделить область, где функция d₁ будет лучшей, - в диапазоне состояний природы Q₁< Q<Q₂. Вторая функция d₂ будет лучшей для состояния природы при Q<Q₁ и при Q>Q₂.

Функция d Î D называется допустимой, если в множестве D* нет никакой другой функции решения d₀, которая была бы лучшей d для всех QÎW. Данная функция для каждого QÎW дол­жна удовлетворять неравенству R (Q, d₀) £ R (Q, d). Таким обра­зом, допустимая функция решения не будет доминирующей стра­тегией статистика в статистической игре.

Рассмотрение только допустимых функций существенно уменьшит множество D* до множества допустимых функций решения.

Отметим, что байесовские функции решения входят в класс допустимых функций.

Определение. Функция решения d₀Î D* называется байесов­ской относительно априорного распределения xÎX состояний природы Q, если она минимизирует байесовский риск r (x, d) на множестве D*.

Таким образом, r (x, d) = r (x, d). Приведем формулу Байеса. Прежде чем ее написать, обратимся к теореме о полной вероятности [2, разд. 2.5, 2.6].

Теорема. Если событие А может наступить только при усло­вии появления одного из событий В₁, В₂,...,B_n, образующих полную группу несовместных событий, то вероятность события А равна сумме произведений вероятностей каждого из событий В₁, В₂,...,B_n на соответствующую условную вероятность собы­тия А:

где P (B_i) - вероятность события B_i;

Р(А|В_i) - условная вероятность события А в случае, если событие В_i уже произошло.

Формула Байеса используется тогда, когда событие А появля­ется совместно с каким-либо из полной группы несовместных событий В₁, В₂,..., B_n. Событие А произошло, и требуется про­извести количественную переоценку вероятностей событий В₁, В₂,..., B_n. При этом известны вероятности Р(В₁), Р(В₂),..., Р (B_n) до опыта (априорные). Требуется определить вероятности после опыта (апостериорные).

Апостериорные вероятности представляют собой условные вероятности Р(В₁|А), Р(В₂|А),..., Р(В_n|А). Вероятность совместно­го наступления событий А с любым из этих событий В_j по тео­реме умножения равна:

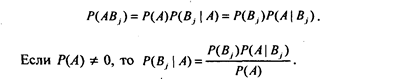
Эту формулу можно переписать исходя из формулы полной вероятности:

Задача 6.1. Собирается партия исправных изделий с трех предприятий. Первый завод поставляет 60 %, второй - 30 %, третий - 10 % изделий. В₁, В₂, В₃ - события, соответствующие тому, что изделия изготовлены на первом, втором и третьем предприятиях.

Вероятность исправной работы изделий первого предприя­тия равна 0,98, второго - 0,99, третьего - 0,96.

Определить вероятность того, что в собранную партию ис­правных изделий попали соответственно изделия с первого, второго и третьего предприятий.

Введем обозначения:

А - событие, заключающееся в том, что изделие исправно;

Р(А) - полная вероятность того, что изделие исправно;

Р(В₁|А), Р(В₂|А), Р(В₃|А) - условные вероятности того, что исправное изделие изготовлено соответственно на первом, вто­ром и третьем предприятиях;

Р(A|В₁), Р(A|В₂), Р(A|В₃) - условные вероятности того, что изделие, изготовленное соответственно на первом, втором и тре­тьем предприятиях, исправно;

Р(В₁), Р(В₂), Р(В₃) - вероятности того, что изделие изготов­лено соответственно на первом, втором и третьем предприятиях.

Известно: Р (А | В₁) = 0,98; Р (А | В₂)= 0,99; Р (А | В₃)= 0,96; Р (В₁) = 0,60; Р (В₂) = 0,30; Р (В₃) = 0,10.

Требуется определить Р(А); Р(В₁|А); Р(В₂|А); Р(В₃|А).

Решение. 1. Определим полную вероятность того, что из­делия, прибывшие с разных предприятии, исправны:

2. Вычислим условные вероятности того, что в партию ис­правных попали изделия с первого, второго и третьего предпри­ятии соответственно:

3. Проверим: Р(В₁|А) + Р(В₂|А) + Р(В₃|А) = 0,599 + 0,303 + + 0,098 = 1.

Вывод. По формуле Байеса количественная переоценка доли предприятии в партии исправных изделии составляет: первое предприятие имеет 59,9 %; второе - 30,3 %; третье - 9,8 %.

Остановимся на некоторых нестандартных принципах при­нятия решений.

Принцип Байеса - Лапласа. Данный принцип отступает СП-условий полной неопределенности. В нем предполагается, что возможные состояния природы могут достигаться с вероятнос­тями Р₁, P₂,..., Р_n при условии, что Р₁+ P₂+,...,+ Р_n = 1. Байес в 1763 г. предложил считать равными вероятности отдельных состояний природы.

В 1812 г. Лаплас обобщил этот принцип на случай различ­ных вероятностей, но тем не менее говорят и о байесовском подходе. Если напомнить, что байесовские функции решения входят в класс допустимых функций, то будет понятно их широ­кое использование в практике принятия решений (см. гл. 3).

Принцип Гурвица. Этот принцип является упрощенным вариантом принципа Байеса - Лапласа. Если известны вероят­ности отдельных состояний, то берут среднее арифметичес­кое результатов при наилучшем решении. Иногда, если суще­ствует возможность определить вес наихудшего и наилучшего решений, то используют их взвешенную среднюю арифмети­ческую.

Проиллюстрируем применение данного принципа на приме­ре строительства предприятий при четырех разных состояниях природы и наличии четырех разных типов предприятий.

Задача 6.2. Имеются определенные средства на возведение предприятий. Необходимо наиболее эффективно использовать капиталовложения с учетом климатических условий, подъезд­ных путей, расходов по перевозкам и т.д. Сочетание этих фак­торов по влиянию на эффективность капиталовложений можно разбить на четыре состояния природы B₁, В₂, В₃, В₄. Типы предприятий обозначим А₁, А₂, А₃, А₄. Эффективность строи­тельства определяется как процент прироста дохода по отно­шению к сумме капитальных вложений. Информацию, отража­ющую постановку задачи, представим в табл. 6.2.

Таблица 6.2

 

Варианты решений

1. Решение по принципу стратегических игр, по принципу максимина: = 4. Нужно строить предприятие А₃.

Изменим условия задачи и предположим, что в табл. 6.2 отражены затраты на строительство предприятий, тогда выбор типа предприятий следует осуществить по принципу минимакса: =9. Нужно строить предприятие А₁ или А₄.

2. Решение по принципу Гурвица.

Если известны все вероятности, определяющие состояния природы, сделаем выбор с помощью среднего арифметического лучшего и худшего результатов.

Согласно табл. 6.2 это будет рекомендация строить предпри­ятие А₂, обеспечивающее максимальную среднюю эффективность Ф = = 8.

3. Применим принцип Байеса при равных вероятностях со­стояний природы Р(В₁)=Р(В₂) = Р(В₃) = Р(В₄) =1/4. Определим рентабельность, соответствующую решению А₁, т. е. М₁:

Далее определяем М₂, М₃, и М₄.

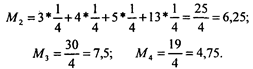
Выводы. Предполагая, что все вероятности состояний при­роды равны, следует строить предприятие А₃, так как M₃ = 7,5 = max (M₁, M₂, M₃, M₄). Отметим, что принцип Байеса-Лапласа имеет смысл применять, если возможно оценить веро­ятности отдельных состояний природы. При этом необходимо, чтобы решения также повторялись многократно.

Когда события повторяются многократно, действует закон больших чисел, согласно которому достигается максимальный средний результат.

При единичных решениях принцип Байеса - Лапласа не следует применять.

Принцип Гурвица фактически является упрощением байесов­ских оценок. Гурвиц допускает, в частности, при отсутствии информации о вероятностях возникновения отдельных состоя­ний природы брать среднее арифметическое значение результа­тов наилучшего и наихудшего решений.

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: