|
Тема 1.1. Случайные события. 1. Случайные события и их классификация. Классификация событий.. 2. Алгебраические действия над событиями.
|
|
|
|
Тема 1. 1. Случайные события
1. Случайные события и их классификация.
2. Алгебраические действия над событиями.
3. Элементы комбинаторики.
4. Классическое и статистическое определения вероятности.
5. Формула полной вероятности. Формула Байеса.
6. Повторные независимые испытания. Формула Бернулли.
7. Предельные теоремы в схеме Бернулли (локальная и интегральная теоремы Муавра-Лапласа).
1. Случайные события и их классификация.
Испытание – это комплекс условий появления какого-либо случайного явления.
Случайным событием называется такой исход испытания (опыта, эксперимента), который может произойти или не произойти.
События обозначаются, как правило, заглавными буквами латинского алфавита A, B, C, D, ….
Частота события – отношение числа наступлений события к числу испытаний.
Вероятность события – мера объективной возможности появления события.
Классификация событий.
Событие называется достоверным, если оно обязательно наступит в результате испытания; достоверное событие обозначается через  .
.
Событие называется невозможным, если оно заведомо не произойдет в результате испытания; невозможное событие обозначается через  .
.
Два события называются несовместными, если появление одного из них исключает появление другого события в одном и том же испытании; в противном случае события называются совместными.
События A1 , A2, …. An  называются попарно-несовместными, если любые два из них несовместны.
называются попарно-несовместными, если любые два из них несовместны.
Два события называются независимыми, если вероятности их наступления не зависят от наступления других событий в данном испытании.
Несколько событий в данном опыте называются равновозможными, если ни одно из них не является объективно более возможным, чем другие (то есть все события имеют равные «шансы»).
|
|
|
События A1, A2, …, An образуют полную группу, если они попарно несовместны и в результате каждого опыта происходит одно и только одно из них.
Противоположным событию 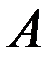 называется событие
называется событие 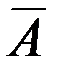 , которое происходит тогда и только тогда, когда не происходит событие
, которое происходит тогда и только тогда, когда не происходит событие 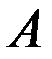 .
.
2. Алгебраические действия над событиями.
|
|
Суммой событий 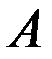 и
и  называется событие
называется событие  , которое происходит тогда и только тогда, когда происходит хотя бы одно из событий
, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий 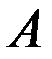 и
и  (то есть или
(то есть или 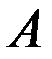 , или
, или  , или оба вместе, знак + читается или ).
, или оба вместе, знак + читается или ).
Приведем пример объединения событий. Пусть два стрелка стреляют в мишень одновременно, и событие А состоит в том, что в мишень попадает 1-й стрелок, а событие B - в том, что в мишень попадает 2-й. Событие С  означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.
означает, что мишень поражена, или, иначе, что в мишень попал хотя бы один из стрелков.
Аналогично суммой конечного числа событий А1, А2, ..., Аk — называется событие А = А1 + А2 + ... + Аk, состоящее в наступлении хотя бы одного из событий Аi (i = 1, 2, ..., k).
Из определения следует, что А + В = В + А.
Справедливо также и сочетательное свойство. Однако А+ А = А (но не 2А, как в алгебре).
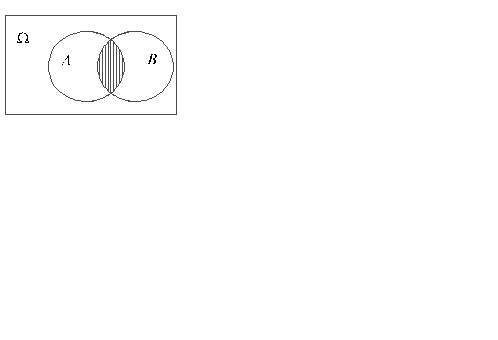
Произведением событий 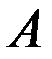 и
и  называется событие
называется событие  , которое происходит тогда и только тогда, когда происходят оба события
, которое происходит тогда и только тогда, когда происходят оба события 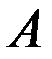 и
и  (знак умножения читается как союз и ).
(знак умножения читается как союз и ).
|
|
На рисунке 3 пересечение событий А и Bизображено в виде заштрихованной области. В условиях приведенного выше примера событие A•B заключается в том, что в мишень попали оба стрелка.
Из определения следует, что АВ = ВА. Справедливы также сочетательный и дистрибутивный законы. Однако
АА = А (но не А2).
|
|
|