 |
Интегральная теорема Лапласа. Тема 1.2. Случайные величины. Понятие случайной величины. Функция распределения.. Дискретная случайная величина.
|
|
|
|
Интегральная теорема Лапласа
Опять предположим, что в каждом из произведенных п испытаний событие А появляется с одинаковой вероятностью р. В прикладных вопросах теории вероятностей наиболее употребимы определения вероятности события А в п испытаниях, когда к изменяется в заданном интервале значений: l < к < m. Соответствующую вероятность обозначают Рп(l, т). Формула для приближенного вычисления этой вероятности устанавливается следующей интегральной теоремой Лапласа.
ТЕОРЕМА 14. 8. Пусть вероятность р наступления события А в каждом испытании постоянна, причем 0 < р < 1. Тогда вероятность того, что событие А появится в п испытаниях от l до т раз, приближенно равна определенному интегралу:


Формула (14. 18), как и (14. 17), применима в случае больших значений п и к. При вычислениях по этой формуле пользуются специальными таблицами для интеграла  поскольку соответствующий неопределенный интеграл не выражается через элементарные функции. Функцию Ф(x) часто называют интегралом ошибок, соответствующая таблица ее значений приведена в Приложении 2. Эта функция является нечетной, поэтому в таблицах обычно приводят значения Ф (x) для положительных значений верхнего предела интегрирования х. Более удобно использовать формулу (14. 18) в виде формулы Ньютона-Лейбница:
поскольку соответствующий неопределенный интеграл не выражается через элементарные функции. Функцию Ф(x) часто называют интегралом ошибок, соответствующая таблица ее значений приведена в Приложении 2. Эта функция является нечетной, поэтому в таблицах обычно приводят значения Ф (x) для положительных значений верхнего предела интегрирования х. Более удобно использовать формулу (14. 18) в виде формулы Ньютона-Лейбница:
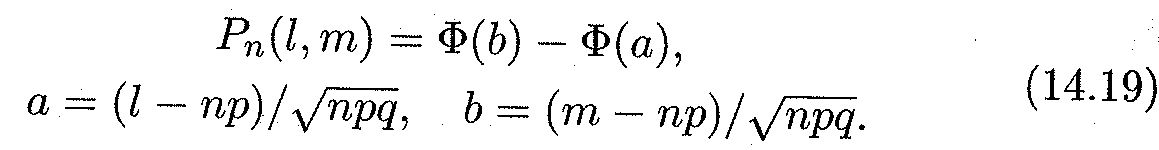
Тема 1. 2. Случайные величины
1. Понятие случайной величины и закон ее распределения.
2. Закон распределения дискретной случайной величины. Многоугольник распределения.
3. Функция распределения и ее свойства.
4. Функция распределения дискретной случайной величины.
5. Плотность распределения и ее свойства.
6. Числовые характеристики случайных величин.
|
|
|
7. Производящая функция.
8. Основные законы распределения случайных величин (биномиальный закон распределения, распределение Пуассона, геометрическое распределение, равномерный закон распределения, показательный закон распределения, нормальный закон распределения).
Понятие случайной величины. Функция распределения.
Случайная величина X- это переменная, которая может принимать в зависимости от исходов испытаний те или иные случайные значения xi. Если все значения случайных величин составляют счетное множество, то случайная величина называется дискретной. Ряд количественных показателей экономических систем могут быть рассмотрены как дискретные случайные величины.
Функцией распределения случайной величины Х называется функция  , которая для любого числа
, которая для любого числа  (множество действительных чисел) равна вероятности события
(множество действительных чисел) равна вероятности события  , то есть
, то есть 
Функция распределения обладает следующими свойствами:
-

-
 - неубывающая функция, то есть
- неубывающая функция, то есть  если
если 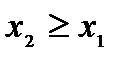 ;
; -
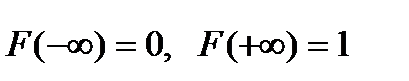 ;
; -
 непрерывна слева в любой точке х, то есть
непрерывна слева в любой точке х, то есть 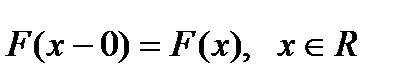 ;
; -
 .
.
Дискретная случайная величина.
Закон распределения случайной дискретной величины - связывает между собой значения случайной величины и вероятности принятия случайной величиной ее значений. Он может быть записан в форме таблицы:
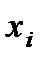
| 
| .. | 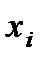
| .. | 
| итого |
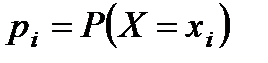
| 
| .. | 
| .. | 
| |
Соответствие между отдельными возможными значениями и их вероятностями называется законом распределения дискретной случайной величины.
Как и в случае функциональной зависимости, этот закон можно задать таблицей, аналитически (формулой) и графически. В случае табличного задания закона распределения дискретной случайной величины соответствующая таблица состоит из двух строк — первая указывает возможные значения, а вторая — их вероятности:
|
|
|
 '
'
Поскольку в одном испытании случайная величина принимает только одно возможное значение, то события Х=х1, Х=х2 - ..., Х=хп образуют полную группу, т. е. сумма их вероятностей равна единице:
p1 +p2 + …+pn = 1.
Если множество возможных значений X дискретной случайной величины бесконечно, то соответствующий ряд вероятностей сходится и его сумма равна единице:
p1 +p2 +…+ pn +…= 1.
Пример 1. В денежной лотерее на 100 билетов разыгрывается один выигрыш в 20 р., два выигрыша по 10 р. и 10 выигрышей по 1 р. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение. Возможные значения X: x1=20, х2 =10, х3=1, х4 =0. Соответственно их вероятности равны: 
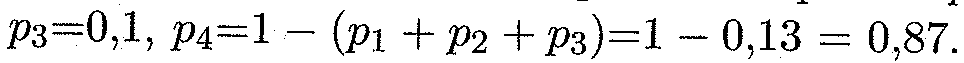 Таким образом искомый закон распределения имеет вид
Таким образом искомый закон распределения имеет вид
X 20 10 1 0
Р 0, 01 0, 02 0, 1 0, 87.
Пример 2. Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение. Случайная величина X — число стандартных деталей среди отобранных — может принимать 4 возможных значения: 0, 1, 2 и 3. Вероятность нахождения к стандартных изделий среди трех отобранных определяется формулой

Варьируя значения к от 0 до 3, получаем искомое распределение:
|
|
|


