 |
5.Формула полной вероятности события. Формула Байеса.
|
|
|
|
5. Формула полной вероятности события. Формула Байеса.
Теорема. Пусть событие B может произойти только с одним из событий  , образующих полную группу попарно несовместных событий, то есть
, образующих полную группу попарно несовместных событий, то есть 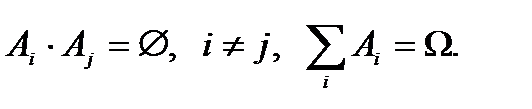 . Тогда вероятность события В вычисляется по формуле полной вероятности:
. Тогда вероятность события В вычисляется по формуле полной вероятности:
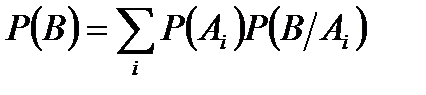
Формула Байеса. Если в результате опыта осуществилось событие В, то вероятность «гипотезы» 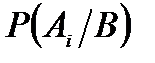 вычисляется по следующей формуле:
вычисляется по следующей формуле:

Пример 6. В магазин поступили соответственно 20, 15, и 10 пальто трех различных фирм. Известно, что доля высококачественных изделий среди продукции первой фирмы в среднем составляет 70%, второй - 80%, третьей – 60%. Наудачу выбранное пальто оказалось плохим. Найти вероятность того, что оно поставлено второй фирмой.
Решение. Для выбранного пальто могут наступить события:  - оно поставлено i–той фирмой, B - оно оказалось плохим. Группа событий:
- оно поставлено i–той фирмой, B - оно оказалось плохим. Группа событий: 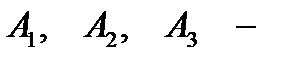 является полной, причем событие B может появиться только вместе с одним из них. По условию задачи:
является полной, причем событие B может появиться только вместе с одним из них. По условию задачи:

Полная вероятность события:
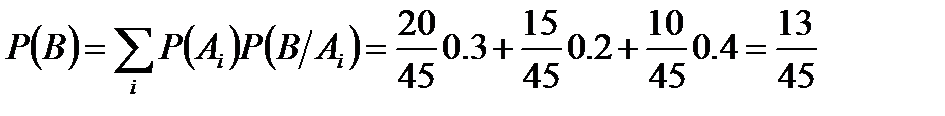 .
.
Выбранное пальто оказалось плохим, наступило событие B. Определим вероятность «гипотезы, состоящей в том, что пальто поставлено в магазин второй фирмой» по формуле:
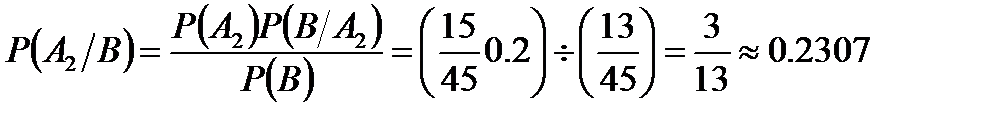 .
.
6. Повторные независимые испытания. Формула Бернулли
Часто практике соответствует схема независимых испытаний Бернулли: проводятся испытания, в которых вероятность появления события 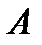 («успеха») одна и та же, а исходы независимы друг от друга.
(«успеха») одна и та же, а исходы независимы друг от друга.
Задача: определить вероятность того, что при 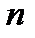 испытаниях событие
испытаниях событие 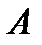 произойдет
произойдет 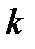 раз (не произойдет
раз (не произойдет  раз). При этом не требуется, чтобы событие
раз). При этом не требуется, чтобы событие 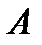 повторялось ровно
повторялось ровно 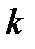 раз в определенной последовательности. Например, при
раз в определенной последовательности. Например, при 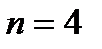 один «успех» может быть реализован следующим образом
один «успех» может быть реализован следующим образом 
 . (Противоположным событию
. (Противоположным событию 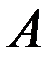 называется событие
называется событие 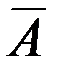 , которое происходит тогда и только тогда, когда не происходит событие
, которое происходит тогда и только тогда, когда не происходит событие 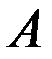 ).
).
|
|
|
Для общего случая вероятность 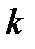 «успехов» из
«успехов» из 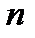 испытаний равна
испытаний равна
 где Cn (k)- число сочетаний из
где Cn (k)- число сочетаний из 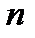 по
по 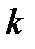 ,
, 
Пример . Вероятность того, что операционные расходы фирмы в течение 1 месяца не превысят установленный бюджет, равна 0, 75. Найти вероятность того, что в ближайшие 6 месяцев операционные расходы в течение 4-х месяцев из них не превысят норму.

7. Предельные теоремы в схеме Бернулли (локальная и интегральная теоремы Муавра-Лапласа).
Локальная теорема Лапласа
Использование формулы Бернулли (14. 16) при больших значениях п и к представляется затруднительным ввиду увеличения объема вычислений и операций с большими числами. В этом случае применима формула, устанавливаемая следующей локальной теоремой Лапласа.
ТЕОРЕМА Пусть вероятность р появления события А в каждом испытании постоянна, причем 0 < р < 1. Тогда вероятность Рп(к) того, что событие А появится в п испытаниях ровно к раз, приближенно равна значению функции φ (х):
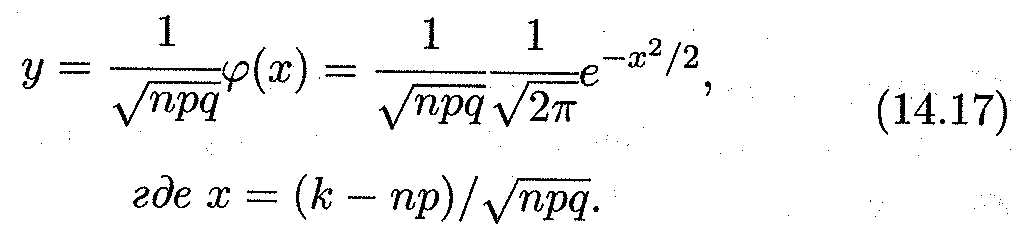
Точность формулы (14. 17) возрастает с увеличением п. Имеются таблицы с вычисленными значениями функции φ {х) (см. Приложение 1. В. Е. Гмурман. ТВ и МС)), по которым можно с достаточно высокой степенью точности найти практически любое значение этой функции, а значит, и вычислить нужную вероятность. Поскольку функция φ (х) четная, то в таблицах даются ее значения только для положительных значений x; иными словами, знак аргумента не играет роли. Формула (14. 17) носит название асимптотической формулы.
Пример 4 . Вероятность выпуска бракованного изделия равна 0, 3. Найти вероятность того, что среди 100 выпущенных изделий будет ровно 60 изделий без брака.
|
|
|
Решение. Вероятность появления события А в одном испытании (изделие без брака) р = 0, 7, тогда q = 0, 3; в нашем случае п = 100, к = 60. Последовательно вычисляем:
 Теперь для найденного аргумента х находим по табл. 1 (см. Приложение) соответствующее значение φ (х); оно равно 0, 0371. Подстановка этого числа в формулу (14. 17) дает приближенное значение искомой вероятности:
Теперь для найденного аргумента х находим по табл. 1 (см. Приложение) соответствующее значение φ (х); оно равно 0, 0371. Подстановка этого числа в формулу (14. 17) дает приближенное значение искомой вероятности:
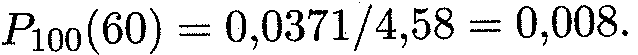
|
|
|


