 |
Основные законы распределения случайных величин
|
|
|
|
X 0 1 2 3
Р 0, 0179 0, 2679 0, 5357 0, 1785.
Пример 3 . Вероятностный прогноз для величины X — процентного изменения стоимости акций по отношению к их текущему курсу в течение шести месяцев — дан в виде закона распределения:
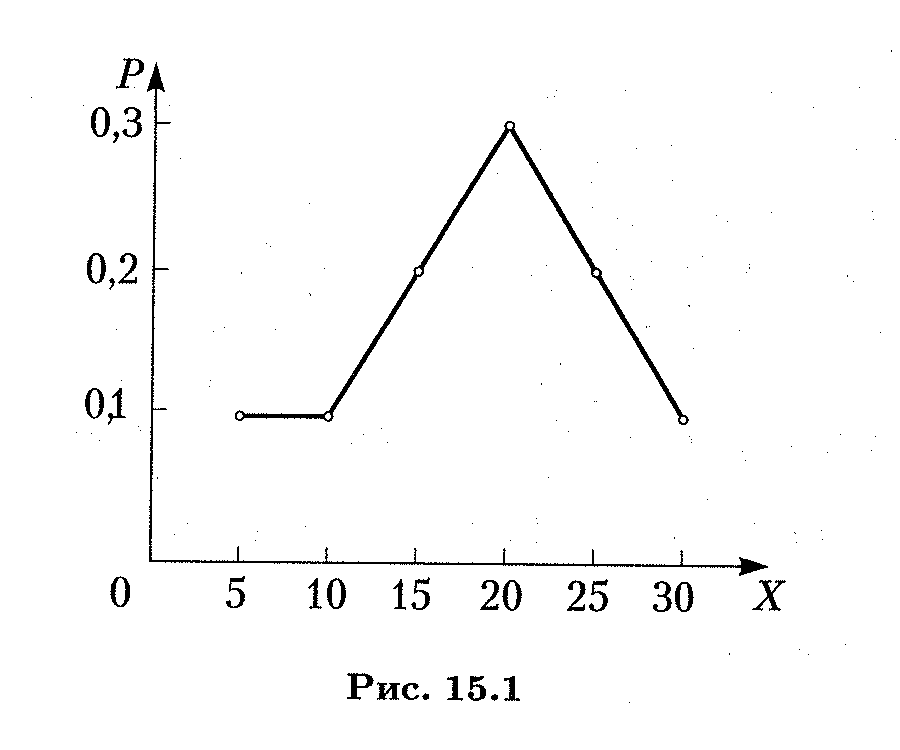
X 5 10 15 20 25 30
Р 0, 1 0, 1 0, 2 0, 3 0, 2 0, 1.
Закон распределения дискретной случайной величины можно изобразить графически, соединив в прямоугольной системе координат ХОP точки (хi, рi ) отрезками прямых. Так, на рис. 15. 1 показан закон распределения из примера 3. Такая фигура называется многоугольником распределения.
Основные законы распределения случайных величин
Биномиальное распределение
Пусть производится п независимых испытаний и в каждом из них событие А может либо появиться, либо не появиться. Пусть также вероятность р появления события А в каждом испытании постоянна (см. раздел 14. 5). В качестве дискретной случайной величины X рассмотрим число появления события А в этих п испытаниях. Очевидно, что х1 =0, х2=1, х3 =2, ..., хп+1=п. Вероятности этих возможных значений к даются формулой Бернулли (см. формулу (14. 16)):
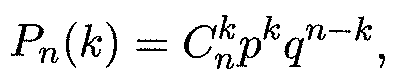(15. 2)
где q = 1 - р — вероятность противоположного события (не появление события А в одном испытании). Формула (15. 2) представляет собой аналитическую форму закона распределения случайной величины (числа появления события А в п независимых испытаниях), который называется биномиальным. Этот закон получил свое название потому, что правая часть в (15. 2) представляет собой общий член разложения бинома Ньютона (14. 2). Таким образом, табличная форма биномиального закона с учетом формулы (15. 2) имеет вид
Можно показать, что сумма всех вероятностей второй отроки этой таблицы равна единице, т. е.
|
|
|
Пример 4 Банк выдает 5 кредитов. Вероятность невозврата, кредита равна 0, 2 для каждого из заемщиков. Составить таблицу закона распределения количества заемщиков, не вернувших кредит по окончании срока кредитования.
Решение. Примем за А событие невозврата кредита. Так как заемщики действуют независимо, то выдачу 5 кредитов можно считать за 5 независимых событий. Вероятность невозврата к кредитов из 5 описывается биномиальным распределением (15. 2), где р = 0, 2, q = 0, 8, к принимает значения от нуля до 5. Искомая таблица закона распределения составляется, согласно (15. 3), при n = 5:
X 5 4 3 2 1 0
Р (0, 2)5 5(0, 2)40, 8 10 (0, 2)3(0, 8)2 10(0, 2)2(0, 8)3 5(0, 2)(0, 8)4 (0, 8)5,
или окончательно:
X 5 4 3 2 1 0
Р 0, 00032 0, 0064 0, 0512 0, 2048 0, 4096 0, 32768.
Распределение Пуассона
Пусть в каждом из п производимых испытаний вероятность появления события А равна р. Как мы знаем, для определения вероятности к появлений события А используется формула Бернулли (15. 2); при больших п пользуются асимптотической формулой Лапласа (14. 17). Однако эта формула плохо подходит для случая, когда р мало. Для случая малых значений р и больших значений п используется асимптотическая формула Пуассона, эта формула выведена при важном допущении, что произведение пр является постоянной величиной, т. е. пр = λ. Тогда вероятность того, что событие А наступит ровно к раз, дается формулой, которая представляет собой закон распределения Пуассона вероятностей массовых и редких (маловероятных) событий.
(15. 4)
Пример 5. На базу отправлено 10 000 изделий. Вероятность того, что изделие в пути получит повреждение, равна 0, 0003. Найти вероятность того, что на базу прибудут 4 поврежденных изделия.
Решение. По условию задачи п = 10 000, р = 0, 0003, к = 4. Находим λ, а затем по формуле (15. 4) и искомую вероятность:
|
|
|
λ = пр= 10000•0, 0003 = 3, 
Числовые характеристики дискретной случайной величины.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности:
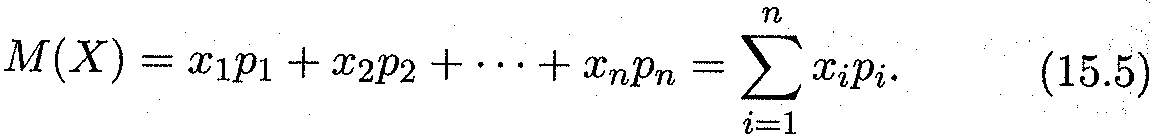
Из этого определения следует, что математическое ожидание есть некоторая постоянная (неслучайная) величина. Вероятностный же смысл математического ожидания состоит в том, что оно приближенно равно (особенно для большого числа испытаний) среднему арифметическому значений случайной величины. Это хорошо видно в случае, когда вероятности всех возможных значений дискретной случайной величины равны:
pi - p = 1/n; из формулы (15. 5) получаем
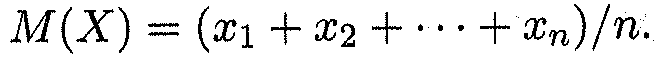(15. 6)
Пример 1 . Найти математическое ожидание количества очков, выпадающих при бросании игральной кости.
РЕШЕНИЕ. Выпадение каждой грани кубика от одного очка до шести имеет одинаковую вероятность р = 1/6. Следовательно, по формуле (15. 6) получаем искомое математическое ожидание:
М(Х) = (1 + 2 + 3 + 4 + 5 + 6)/6 = 3, 5.
Пример 2. Найти математическое ожидание числа невозврата кредитов по данным примера 4 п. 15. 1.
Решение. Воспользуемся итоговой таблицей распре деле ния дискретной случайной величины, полученной в этом примере, и формулой (15. 6); находим
М(Х) = 5 • 0, 00032 + 4 • 0, 0064 + 3 • 0, 0512+
|
|
|
