Свойства математического ожидания

+2 • 0, 2048 + 1 • 0, 4096 + 0 • 0, 32768 = 1.

Свойства математического ожидания

Математическое ожидание обладает рядом свойств, кото­рые указаны ниже.

Свойство 1. Математическое ожидание постоянной вели­чины С равно этой постоянной:

М(С) = С.

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:

М(СХ) = СМ(Х).

Свойство 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий:

М(Х1 + Х2 + • • • + Хт) = М(Х1) + М(Х2) + • • • + М(Хт).

Свойство 4. Математическое ожидание произведения независимых случайных величин равно произведению их ма­тематических ожиданий:

М(Х1 Х2... Хт) = М(Х1)М(Х2)... М(Хт).

Пример 3. Пусть ежедневные расходы на обслуживание и ре­кламу автомобилей в некотором автосалоне составляют в сред­нем 100 тыс. р., а число продаж X автомашин в течение дня подчиняется следующему закону распределения:

       X 0 12 3 4 5 6    7       8      9

       Р 0, 25 0, 2 0, 1  0, 1  0, 1  0, 1 0, 05 0, 05 0, 025 0, 025..

Так как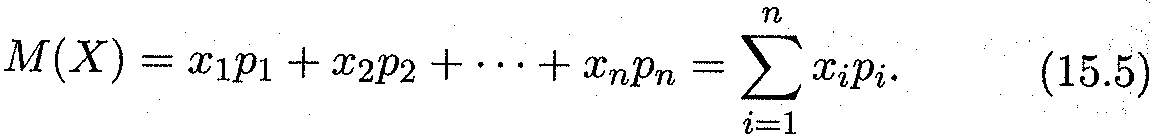  

то М(Х) = 0, 2 +0, 2 + 0, 3 + 0, 4 + 0, 5 + 0, 3 + 0, 35 +0, 2 + 0, 0225 = 2, 675  

Найти математическое ожидание ежедневной прибыли при цене на машину 150 тыс. р.

Решение. Ежедневная прибыль подсчитывается по фор­муле

П = (150Х — 100) тыс. р.

Искомая характеристика М(П) находится с использованием указанных выше свойств математического ожидания (в тыс. р. ):

М(П)=М(150Х—100)=150М(Х) —100=150 • 2, 675-100=301, 25.

Если в п независимых испытаниях вероятность появления в каждом из них события А постоянна, то ответ на вопрос о сред­нем числе появления события А дает следующая теорема.

ТЕОРЕМА 15. 1. Математическое ожидание М(Х) числа появлений события А в п независимых испытаниях равно про­изведению числа испытаний на вероятность появления собы­тия в каждом испытании:

М(Х) = пр. (15. 7)

Пример 4• Найти математическое ожидание числа выигрыш­ных лотерейных билетов, если вероятность выигрыша по одному билету равна 0, 015, причем куплено 200 билетов.

Решение. Поскольку приобретение каждого билета яв­ляется независимым испытанием относительно появления со­бытия А — выпадения выигрыша, то здесь применимы теоре­ма 15. 1 и формула (15. 7). В нашем случае п = 200, р = 0, 015, откуда мы получаем

М(200) = 200 • 0, 015 = 3.

 

Дисперсия дискретной случайной величины

Как уже говорилось выше, математическое ожидание яв­ляется средней характеристикой случайной величины. Однако оно не характеризует случайную величину достаточно полно, и по этой причине рассматриваются и другие числовые харак­теристики. Пусть X — случайная величина, а М (X) — ее ма­тематическое ожидание.

Определение 2. Разность между случайной величиной и ее математическим ожиданием называется отклонением.

Пусть закон распределения случайной величины X дается формулой (15. 1), тогда отклонение Х—М(Х) имеет следующий закон распределения:

Отклонение имеет важное свойство, которое устанавливается непосредственно из свойств математического ожидания:

т. е. математическое ожидание отклонения равно нулю.

Пример 5. По данным примера 3 найти закон распределения отклонения числа проданных за день автомашин.

Решение. Как было подсчитано в примере 3, М(Х) = 2, 675. Тогда, согласно (15. 8), искомый закон определяется следующей таблицей:

На практике важной характеристикой является рассеяние¹ возможных значений случайной величины вокруг ее среднего значения. Среднее значение отклонения, согласно (15. 9), рав­но нулю, так как суммируются отрицательные и положитель­ные отклонения (см. пример 5), поэтому целесообразно ввести в рассмотрение абсолютные значения отклонений или их квад­раты.

 

Определение 3. Математическое ожидание квадрата откло­нения называется дисперсией или рассеянием:

D(X) = M[X-M(X)]².        (15. 10)

Пусть случайная величина задана законом распределения (15. 1), тогда квадрат отклонения этой случайной величины имеет следующий закон распределения:

[Х-М(Х)]² [x₁ –М(Х)]² [х₂-М(Х)]²... [х_п-М(Х)]²

Р      P₁   Р₂.         .. р_п.

Отсюда, согласно формуле (15. 10), получаем формулу диспер­сии в развернутом виде:

D{X) = [x₁ -M (X)]²p₁  + [х₂ - M(X)]²p₂ +... + [х_п - М(Х)]²р_п.

При вычислении дисперсии часто бывает удобно воспользо­ваться формулой, которая непосредственно выводится из фор­мулы (15. 10):

D(X) = М(Х²) - [М(Х)]².   (15. 11)

Пример 6. Найти дисперсию ежедневной продажи числа автомашин по данным примера 3.

Решение. Закон распределения случайной величины Х² имеет вид

X² 0 1  4  9   16 25   36   49   64 81

Р 0, 25 0, 2 0, 1 0, 1    0, 1 0, 1 0, 05 0, 05 0, 025 0, 025.

Математическое ожидание М(Х²) подсчитывается из этой таб­лицы:

М(Х²) = 0 • 0, 25 + 1 • 0, 2 + 4 • 0, 1 + 9 • 0, 1 + 16 • 0, 1 + 25 ■ 0, 1-1 +36 • 0, 05 + 49 • 0, 05 + 64 • 0, 025 + 81 • 0, 025 = 13, 475.

Математическое ожидание М(Х) = 2, 675. Следовательно, согласно формуле (15. 11), получаем искомую величину дис­персии:

D(X) = М(Х²) - [М(Х)]² = 13, 475 - 7, 156 = 6, 319.

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: