Свойства дисперсии. Среднее квадратическое отклонение

Свойства дисперсии

Приведем здесь основные свойства дисперсии.

Свойство 1. Дисперсия постоянной величины С равна, нулю:

D(C) = 0.

Свойство 2. Постоянный множитель можно выносить на знак дисперсии, возводя его в квадрат:

   D(CX)  = C²D(X). (15. 12)

Свойство 3. Дисперсия алгебраической суммы независи­мых случайных величин равна сумме их дисперсий:

D(X₁+X₂+... +X_n)=D(X₁)+D(X₂)+... +D(X_n).            

Перечисленные свойства дисперсии используются при вы­числениях, когда мы имеем дело с несколькими случайны­ми величинами. Из свойств 1 и 3 следует важный вывод:

D(X + С) = D(X), где С — постоянная величина. Кроме того, справедлива следующая теорема.

ТЕОРЕМА 15. 2. Дисперсия числа появления события А в п независимых испытаниях с вероятностью появления р в каждом из них этого события вычисляется по формуле

D(X) = пр(1 - р) = npq.   (15. 14)

Приведем здесь еще два важных результата: для случай­ной величины, распределенной по закону Пуассона ( 15. 4 ( пр = λ ) ), ма­тематическое ожидание и дисперсия равны параметру данного распределения.

Пример 7. Найти дисперсию числа выигрышных лотерейных билетов, если вероятность выигрыша по одному билету равна 0, 015, причем куплено 200 билетов.

Поскольку приобретение каждого билета яв­ляется независимым испытанием относительно появления со­бытия А — выпадения выигрыша, то здесь применимы теоре­ма 15. 1 и формула (М(Х) = пр. 15. 7). В нашем случае п = 200, р = 0, 015, откуда мы получаем М(200) = 200 • 0, 015 = 3.

Решение. Имеем 200 независимых испытаний с вероятно­стью появления выигрышного билета р = 0, 015. Стало быть, q = 1 — 0, 015 = 0, 985, откуда и получаем искомую дисперсию:

D{X) = npq = 200 • 0, 015 • 0, 985 = 2, 955.

Пример 8. Банк выдал ссуды п разным заемщикам в размере S р. каждому под ставку ссудного процента r. Найти математи­ческое ожидание и дисперсию прибыли банка, а также условие на ставку ссудного процента, если вероятность возврата ссуды заемщиком равна р.

Решение. Поскольку заемщики между собой не связаны, то можно полагать, что мы имеем п независимых испытаний. Вероятность утери ссуды для банка в каждом испытании рав­на q = 1 —р. Пусть X — число заемщиков, возвративших ссуду с ссудным процентом, тогда прибыль банка определяется формуле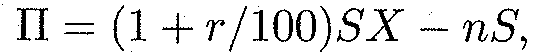   

где X является случайной величиной с биномиальным зако­ном распределения. Тогда, согласно теореме 15. 1, математическое ожидание прибыли определяется с использованием фор мулы (15. 7):

М(П) = (1+г/100) SM(X) — nS =  (1 + r/100)Snp — Sn = Sn(rp/100 - q).

Поскольку выдача ссуды имеет смысл лишь при положительном математическом ожидании прибыли (положительная сред­няя величина прибыли), то из условия М(П) > 0 вытекает условие на ставку ссудного процента:

г > 100q/p, или г > 100(1 -р)/р.

Дисперсия прибыли банка находится, согласно теореме 15. 2, с использованием формулы (15. 14) и свойств 1-3:

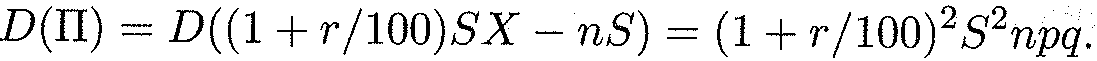
Среднее квадратическое отклонение

Одной из основных оценок рассеяния возможных значе­ний случайной величины служит среднее квадратическое от­клонение.

Определение 4. Средним квадратическим отклонением слу­чайной величины X (стандартом) называется квадратный ко­рень из ее дисперсии:

(15. 15)

Согласно этому определению, из свойства 3 и формулы (15. 13) следует, что в случае суммы взаимно независимых слу­чайных величин справедлива формула

Пример 9. Найти дисперсию и среднее квадратическое откло­нение случайной величины X, заданной следующим распреде­лением:

X    -5    2     3     4     6

р     0, 1 0, 2 0, 3      0, 3 0, 1

Решение. Имеем М(Х) = 2, 6. Составим таблицу распре деления случайной величины X²:

X² 25   4 9     16 36

р 0, 1 0, 2   0, 3    0, 3   0, 1.

Отсюда получаем, что М(Х²) = 14, 4. По формулам (15. 11) и (15. 15) окончательно получаем искомые значения D(X) н σ (Х):

D(X) = М(Х²) - [М(Х)}² = 7, 64, σ (Х) = = 2, 76.

Пример 10. Законы распределения независимых случайных величин X и Y приведены соответственно в таблицах:

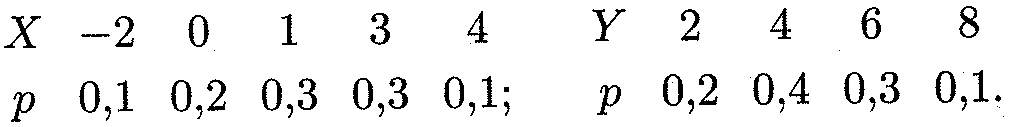
Найти дисперсию и среднее квадратическое отклонение случайной величины

Z = 2Х + 3У.

Решение. Согласно свойствам 2 и 3 дисперсии (формулы (15. 12) и (15. 13)), имеем

D(Z) = D(2X + ЗУ) = 4 D(X) + 9 D(Y).

Для вычисления дисперсий D(X) и D(Y) составляем соответствующие таблицы — законы распределения случайных вели чин X² и Y²:

X²    4     0     1     9     16   Y²     4   16   36   64

р      0, 1  0, 2  0, 3  0, 3  0, 1; р      0, 2  0, 4  0, 3  0, 1.

Отсюда получаем

D(X) = М(Х²)-[  М(Х)]² = 5 - 1, 4² = 3, 04;

D(Y) = М(У²) - [М(У)]² = 24, 4 - 4, 6² = 3, 24.

 

Искомые дисперсия и среднее квадратичное отклонение слу­чаемой величины Z равны:

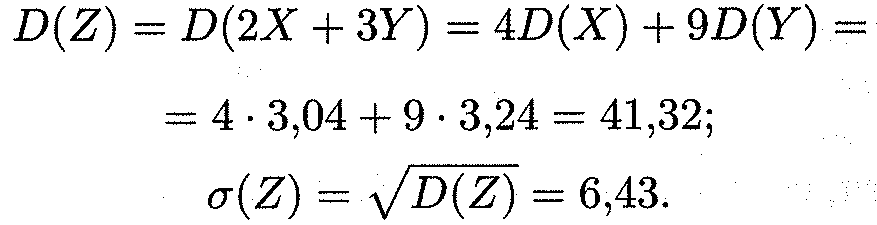
Пример 11. В условиях примера 8 найти математическое ожидание и среднее квадратическое отклонение прибыли при n = I ООО, р = 0, 8, S = 100 тыс. р. и r = 30%.

Решение. Ставка ссудного процента удовлетворяет условию, чтобы математическое ожидание прибыли было положительным:

30 > 100(1 — 0, 8)/0, 8, Математическое ожидание при­были:

Среднее квадратическое отклонение прибыли:

 

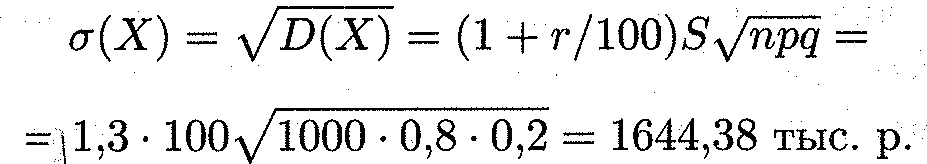
При расчетах дисперсии используют свойство: .

Для биноминально распределенных случайных величин можно применять известные формулы расчета характеристик:

; .

; .

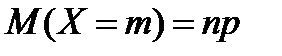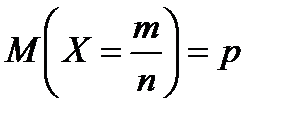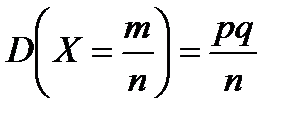3. 1. 10. Основные операции над случайными дискретными величинами:

1. Умножение случайной величины на число a:

,      ;

где .

1. Суммирование случайных величин:

, ;

Где ;  .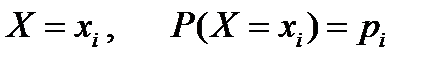

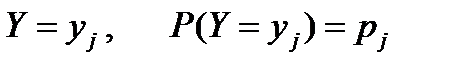1. Умножение случайных величин:

,    ;

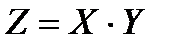где ;  .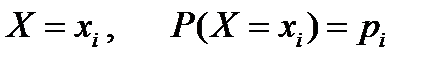

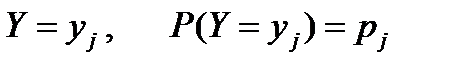Пример 1. Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0, 1. Составить закон распределения числа возвращенных в срок кредитов из 5 выданных. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины.

Решение. Для каждого выданного кредита может наступить одно из событий: он не возвращен -  или возвращен – А, по условию задачи с вероятностями . Вероятности событий неизменны для всех кредитов, следовательно, имеют место независимые повторные испытания, число которых мало .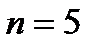

Х - случайная величина, а именно, число возвращенных кредитов. Рассмотрим событие , а именно - событие В_m, состоящее в том, что событие A наступит в n независимых испытаниях m=0, 1, 2, 3, 4, 5  раз. Для определения вероятности данного события следует применять формулу Бернулли: 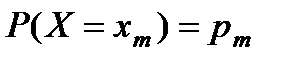= 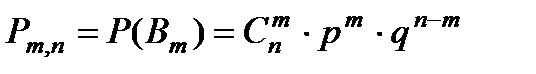. Случайная величина имеет биномиальный закон распределения:

 

	=
	=
	=
	=
	=
	=

 

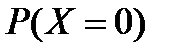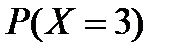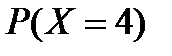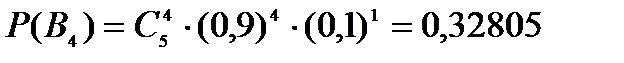
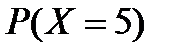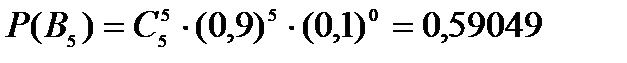
Характеристики биномиально распределенной случайной величины можно найти, используя известные формулы:

Математическое ожидание - .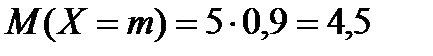

Дисперсия - .

Найдем вероятность события -  В, состоящее в том, что число возвращенных кредитов не менее двух, т. е. или 2, или 3, или 4 или 5:

;

 

Пример 2. В населенном пункте три рынка. Вероятность того, что на рынке есть необходимый для господина N товар, равна 0. 6. Он пытается купить этот товар. Если на очередном рынке отсутствует данный товар, господин отправляется за ним на следующий рынок. Поиски прекращаются либо с приобретением товара, либо после того как посещены все рынки. Составить закон распределения числа посещенных рынков. Построить функцию распределения найти математическое ожидание, дисперсию и среднее квадратическое отклонение числа посещенных рынков.

Решение. Х – число посещенных рынков. А_i – событие, состоящее в том, чтона i-том посещенном рынке есть необходимый товар, - отсутствует. Вероятности этих событий: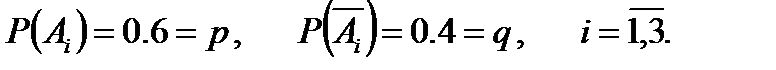

Закон распределения и рабочие расчеты по характеристикам случайной величины:

xi		xi pi	xi2 pi
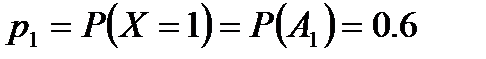
		0. 6	0. 6
		0. 48	0. 96
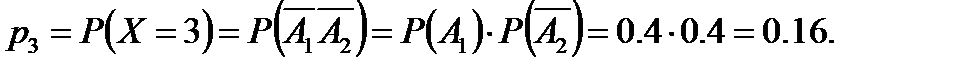
		0. 48	1. 44
å	1. 0	1. 56	3. 0

 

Характеристики случайной величины – числа посещенных рынков:

Математическое ожидание - .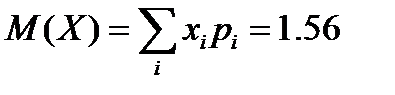  

Дисперсия - .

Среднее квадратическое отклонение - .

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: