 |
Спектры периодических функций
|
|
|
|
МП-реле (часть 2) Рис. и формулы к лекциям
Спектры периодических функций
Гармонический ряд в тригонометрической форме:
(2. 1)
где коэффициенты
(2. 2)
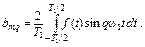(2. 3)
Здесь а0/2 – постоянная слагающая; amq и bmq – амплитуды косинусоидальных и синусоидальных членов ряда.
знакопеременная прямоугольная функция
Для (рис. 2. 1) в разложении в ряд Фурье отсутствуют постоянная составляющая, все косинусоиды и чётные синусоиды. Выполняется условие периодичности f(t)=f(T1/2-t); определение коэффициентов bmq:
т. е.
.
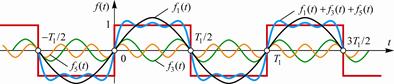
Рис. 2. 1. Слагающие ряда Фурье периодической знакопеременной функции
другая тригонометрическая форма записи ряда Фурье, в результате объединения функций синуса и косинуса одной частоты в выражении (2. 1):
(2. 4)
где амплитудный и фазовый коэффициенты
.
Комплексная или экспоненциальная форма ряда Фурье, которая может быть получена на основе формул Эйлера:
С использованием этих соотношений заключенное в скобки в формуле (2. 1) выражение приводится к виду
,
а ряд Фурье записывается следующим образом:
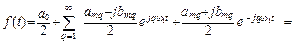
(2. 5)
В выражении (2. 5) сопряжённые комплексные коэффициенты каждой q-й гармоники
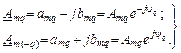(2. 6)
Функция amq относительно q чётная, а bmq – нечётная, т. е. amq сохраняет свой знак, а bmq меняет его: amq=аm(-q), bmq=-bm(-q). Обе суммы в выражении (2. 5) можно заменить суммированием по одной экспоненте при изменении индекса q в пределах от –¥ до +¥ (включая q=0) с учётом того, что
|
|
|
,
получая в результате комплексную форму ряда Фурье:
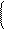
. (2. 7)
Комплексные амплитуды ряда Фурье вида (2. 7) вычисляются после подстановки в (2. 6) выражений (2. 2) и (2. 3):
F mq 
, (2. 8)
где Am0=a0;
амплитуды синусных и косинусных гармоник
.
Вычисления модуля и аргумента комплексных чисел
являются также соответственно чётной и нечётной функциями частоты.
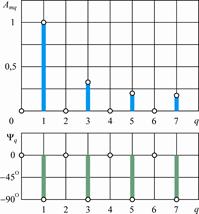
Пример 2. 1. Задана периодическая функция
Построить графики амплитудного и фазового спектров функции.
Согласно соотношениям (2. 1) комплексные коэффициенты суммы в экспоненциальной форме зависят от кратности q:
A m0=0; A m1=-j=e-j90o; A m3= 
»0, 33e-j90o; A m5= 
=0, 2e-j90o;
A m7 = 
»0, 14e-j90o. Расстояния между соседними линиями амплитудного и фазового спектров равны значению ω 1 (рис. 2. 2). Оба спектра, зависящие от дискретных значений частоты qω 1, дают данные обо всех гармониках и полностью определяют исходную периодическую функцию f(t).
|
Рис. 2. 2. Спектры периодической функции f(t)=sinw1t+ sin3w1t/3+ +sin5w1t/5+sin7w1t/7 |
Выражение (2. 8) удобно рассматривать как прямое преобразование непрерывной периодической временнό й функ-ции в комплексную спек-тральную функцию дискретных значений частоты.
Выражение (2. 7), определяющее сумму бесконечного числа гармоник, кратных частоте ω 1, представленных экспонентами с мнимым аргументом и комплексными коэффициентами, – как обратное преобразование дискретного частотного спектра в периодическую временнý ю функцию. При этом дискретная частотная функция Amq(qω 1) полностью определяет периодическую временнý ю функцию и является её эквивалентной спектральной формой.
Примечание: здесь и далее используем математические паекты Matlab, MathCad, либо Excel.
|
|
|
Пример 2. 2. Определить коэффициенты разложения в ряд Фурье периодической последовательности прямоугольных импульсов единичной амплитуды и длительности tи, следующих с периодом Т1 (рис. 2. 3).
Коэффициенты ряда Фурье вычисляются по формуле (2. 8) с использованием формул Эйлера:
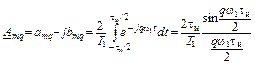. (2. 9)
Коэффициенты А mq вещественны, ряд содержит только косинусные члены, т. е. временнá я функция является чётной. Когда q=0, А mq=2tи/Т1, т. е. постоянная составляющая а0/2=tи/Т1.
Ряд Фурье с учётом значений коэффициентов даёт временнý ю функцию f(t) в виде
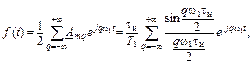(2. 10)
амплитудный спектр
ï F mqï 
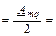
. (2. 11)
Огибающая амплитудного спектра изменяется по закону | sinx/x |. Узлы огибающей определяются текущими значениями частоты wуз, обращающими sinx в нуль (кроме q=0, когда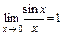 
): wуз=2pn/tи, где n=1, 2, 3, …. На рис. 2. 3 показан амплитудный спектр, являющийся чётной функцией, когда Т1=20мс (50 Гц), а Т1/tи=4.
Рис. 2. 3. Импульсная периодическая функция и её амплитудный спектр
Число гармоник на интервале между двумя узлами равно отношению 2p/tиw1=Т1/tи.
Фаза комплексного коэффициента А mq принимает или нулевое значение на интервалах, где результат, вычисляемый по (2. 10), положителен, или p, где результат отрицателен.
|
|
|
