Главная | Обратная связь | Поможем написать вашу работу!

Спектры дискретных сигналов. Процедура получения дискретизированного сигнала

⇐ ПредыдущаяСтр 6 из 7Следующая ⇒

Спектры дискретных сигналов

Дельта-функция и её свойства

Дельта-функция аналитически записывается как

(2. 28)

Площадь импульса d(t) всегда равна единице:

. (2. 29)

При сдвиге дельта-функции по оси времени из точки t=0 в точку t=t_d выражения (2. 28) и (2. 29) приобретают обобщённую форму:

(2. 30)

. (2. 31)

Если имеется некоторая непрерывная функция f(t), значение которой в точке t=t_d равно f(t_d), то на основании (2. 30) и (2. 31) справедливо соотношение, характеризующее фильтрующее свойство дельта-функции [13]:

. (2. 32)

Спектральная плотность дельта-функции определяется с помощью прямого преобразования Фурье (2. 17):

(2. 33)

Рис. 2. 13. Амплитудный и фазовый спектры дельта-функции

Процедура получения дискретизированного сигнала

Процедуру получения дискретизированного сигнала u_д(t):

u_д(t)=u(t)´ y(t). (2. 34)

Рис. 2. 14. Дискретизация сигнала

По (2. 7) и (2. 10) представляется рядом Фурье в виде

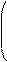
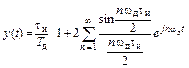, (2. 35)

где w_д=2p/Т_д – частота дискретизации.

После подстановки правой части формулы (2. 35) в соотношение (2. 34) получается выражение для функции, определяющей характер изменения дискретизированного сигнала:

. (2. 36)

Первому слагаемому соответствует спектральная плотность S(w) исходного сигнала u(t) [21]. К произведению u(t)e^j^q^w^д^t второго слагаемого можно применить прямое преобразование Фурье:

В выражении для S(jw)_II первый интеграл представляет собой спектральную плотность сигнала u(t) на частотах w-nw_д, а второй – ту же спектральную плотность, но на частотах w+nw_д:

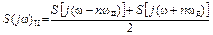. (2. 37)

Следовательно, дискретизированному сигналу вида (2. 36) соответствует спектральная плотность

. (2. 38)

Рис. 2. 15. Спектры сигналов:

а – непрерывного; б – дискретизированного

виртуальная бесконечная последовательность n дельта-функций:

формула (2. 34) запишется следующим образом:

. (2. 39)

Выражение (2. 38) для спектральной плотности дискретного сигнала в этом случае примет вид

. (2. 40)

спектральную плотность S _д(w) непосредственно по совокупности временных отсчётов u(nT_д)

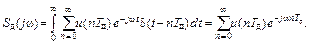(2. 41)

Рассмотрим импульс напряжения, имеющий вид одного периода синусоиды единичной амплитуды частоты 50Гц – u(t)=sin(w₁t+y_u), который дискретизирован четырьмя равноотстоящими выборками, первая из которых осуществляется в момент t=-y_u/w₁ (рис. 2. 12, а). Оценим влияние на спектр дискретизированного сигнала моментов взятия отсчётов.

Для определения спектра воспользуемся формулой (2. 41), которая в данном случае принимает вид

Интервал дискретизации Т_д=5мс (w_д=1256с^-¹), следовательно, один период синусоиды будет представлен двумя отсчётами, так как u(0)=0, u(Т_д)=1, u(2Т_д)=0, u(3Т_д)=-1.

Обозначив кратность текущего значения частоты относительно w₁ как q=w/w₁, получаем

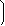
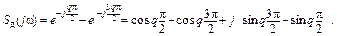
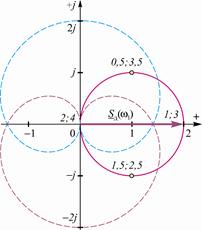
Отображение спектральной плотности S_д(jw) в комплексной плоскости для положительных значений w даёт годограф вектора S (w) (рис. 2. 16, где числа соответствуют значениям кратности q и указывают положение конца вектора S _д(w) на разных частотах).

Годограф комплексной величины S_д(jw) в диапазоне изменения кратности 0£ q£ 2 имеет форму " яблока", симметрично размещённого относительно вертикальной оси в четырёх квадрантах: значению q=0 соответствует нулевой вектор S _д(0)=0× e^j^p^/², а q=1 – вектор S _д(w₁)=2e^-^j^p^/² (на правой половине годографа точкой отмечено положение конца вектора при q=0, 5); значению q=2 соответствует вектор S _дw₂)=0× e^j^p^/² (на левой половине годографа точкой отмечено положение конца вектора при q=1, 5). В диапазоне 2£ q£ 4 годограф имеет зеркально отражённую форму: значению q=2 соответствует вектор S _д(w₂)=0× e^-^j^p^/², а q=3 –

Рис. 2. 16. Спектральная плотность периода

синусоиды при u(0)=0, u(Т_д)=1,

u(2Т_д)=0, u(3Т_д)=-1

S _д(w₃)=2e^j^p^/² (на левой половине годографа точкой отмечено положение конца вектора S _д(w) при q=2, 5); значению q=4 соответствует вектор S _д(w₄)=0× e^-^j^p^/² (на правой половине годографа точкой отмечено положение конца вектора S _д(w) при q=3, 5). Указанный диапазон изменения кратности q соответствует одному циклу изменения спектральной плотности одного периода дискретизированной синусоиды.

Из выражения для S_д(jw) после преобразований легко получить формулы для вычисления амплитудного и фазового спектров:

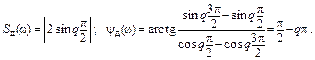
Графики модуля и фазы комплексной величины S_д(jw) (амплитудный и фазовый спектры) показаны на рис. 2. 17.

Можно показать, что амплитудный спектр симметричен относительно частоты w=0. Фазовый спектр имеет линейный характер со скачкообразным изменением фазы от -p/2 до +p/2 в узлах, определяемых нулевым и целыми чётными значениями кратности: q=0, ±2, ±4…; скачок фазы увеличивается в 2 раза при q=±1, 5, ±2, 5 и т. д.

Как уже отмечалось в примере 2. 6, выборки могут и не попадать на нулевые значения синусоиды, тогда они не будут попадать и на экстремумы синусоиды. Общее число членов ряда (2. 41) при этом станет в 2 раза больше, так как u(0)¹ 0, u(2Т_д)¹ 0.

Рис. 2. 17. Амплитудный и фазовый спектры одного периода синусоиды

при u(0)=0, u(Т_д)=1, u(2Т_д)=0, u(3Т_д)=-1

Пусть " нулевая" выборка u(0)=0, 5, т. е. w₁t+y_u=p/3; остальные три выборки – u(Т_д)=0, 866; u(2Т_д)=-0, 5; u(3Т_д)=-0, 866. Для таких исходных данных спектральная плотность вычисляется по формуле

Отображение спектральной плотности S_д(jw) для положительных w в этом случае показано на рис. 2. 18, где числа также соответствуют значениям кратности q и указывают положение конца вектора S _д(w) на разных частотах.

Годограф комплексной величины S_д(jw) в диапазоне изменения кратности 0£ q£ 2 также имеет форму " яблока", размещённого в четырёх квадрантах, но расположение годографа асимметрично

Рис. 2. 18. Функция S_д(jw) периода

синусоиды при u(0)=0, 5; u(Т_д)=0, 866;

u(2Т_д)=-0, 5; u(3Т_д)=-0, 866

относительно оси мнимых чисел. Значениям кратности q=0, q=1 и q=2 соответствуют вектора S _д(0)=0× e^j^p^/², S _д(w₁)=2e^-^j^p^/³, S _д(w₂)=0× e^j^p^/² (на кривой годографа точками отмечено положение конца вектора S _д(w) при q=0, 5 и q=1, 5). В диапазоне 2£ q£ 4 годограф имеет зеркально отражённую форму: значениям q=2 и q=4 соответствует вектор S _д(w₂)=S _д(w₄)=0× e^-^j^p^/², а q=3 – S _д(w₃)=2e^j^p^/3 (на кривой годографа точками отмечено положение конца вектора S _д(w) при q=2, 5 и q=3, 5).

Таким образом, момент формирования выборки u(0) оказывает существенное влияние на спектральную плотность S_д(jw), и её отображение в комплексной плоскости изменяется по сравнению со случаем, когда u(0)=0 (рис. 2. 16). Следовательно, должны измениться амплитудный и фазовый спектры, формулы для вычисления которых получаются из выражения, описывающего спектральную плотность S_д(jw):

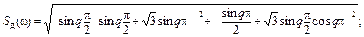
Амплитудный спектр, когда выборки u(0)=0, 5; u(Т_д)=0, 866; u(2Т_д)=-0, 5; u(3Т_д)=-0, 866, довольно сильно отличается от амплитудного спектра аналогичного исходного сигнала (рис. 2. 19), но вычисленного по значениям u(0)=0; u(Т_д)=1; u(2Т_д)=0; u(3Т_д)=-1 (штриховая линия). Максимумы S_д(w_{0, 8})=S_д(w_{3, 2})»2, 14

Рис. 2. 19. Амплитудный и фазовый спектры одного периода синусоиды

при u(0)=0, 5; u(Т_д)=0, 866; u(2Т_д)=-0, 5; u(3Т_д)=-0, 866

превышают значение S_д(w)=2, которое точнее соответствует исходному сигналу. Из-за этого и появляется неточность при восстановлении сигнала по дискретным отсчётам (см. рис. 2. 12, в, г).

Различия фазовых спектров заключается в том, что когда u(0)=0, 5; u(Т_д)=0, 866; u(2Т_д)=-0, 5; u(3Т_д)=-0, 866, фазовый спектр, во-первых, приобретает нелинейный характер; во-вторых, скачки фазы от -p/2 до +p/2 отсутствуют, а скачки фазы от -p до p происходят в узлах, определяемых не кратными целым значениям текущей частоты w (q»-0, 33; q»1, 67 и q»2, 33).

На основании полученных результатов можно предположить, что бό льшее смещение выборки u(0) к амплитуде исходного сигнала сильнее " искажает" спектральную плотность S_д(jw).

Пусть " нулевая" выборка u(0)=0, 866, т. е. w₁t+y_u=2p/3; остальные три выборки – u(Т_д)=0, 5; u(2Т_д)=-0, 866; u(3Т_д)=-0, 5. Тогда формула для определения спектральной плотности рассматриваемого сигнала принимает вид

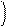
Отображение спектральной плотности S_д(jw) для положительных w в этом случае показано на рис. 2. 20.

Рис. 2. 20. Функция S_д(jw) периода синусоиды при u(0)=0, 866; u(Т_д)=0, 5; u(2Т_д)=-0, 866; u(3Т_д)=-0, 5

Годограф комплексной величины S_д(jw) в диапазоне изменения кратности 0£ q£ 2 приобретает вид окружности неправильной формы, размещённой в четырёх квадрантах, причём 2-й и 3-й квадранты годограф захватывает весьма незначительно: если q=1, 8, вектор S _д(w_1,₈)»0, 26e^-^j⁹⁴^О, q=2, 2 – S _д(w_2,₂)»0, 26e^j⁹⁴^О; на нулевой частоте S _д(0)=0× e^j^p^/², если q=1 и q=2 то S _д(w₁)=2e^-^j^p^/⁶, S _д(w₂)=0× e^j^p^/² (точками отмечено положение конца вектора S_д(w) при q=0, 5 и q=1, 5). В диапазоне 2£ q£ 4 значения кратности q=2 и q=3 дают S _д(w₂)=0× e^-^j^p^/² и S _д(w₃)=2e^j^p^/⁶ (на годографе точками отмечено положение конца вектора при q=2, 5, q=3, 5); предельному значению полного цикла изменения q соответствует S _д(w₄)=0× e^-^j^p^/².

В целом годограф спектральной плотности S_д(jw) ещё сильнее отличается от случая, когда выборки u(Т_д) и u(2Т_д) попадают на экстремумы синусоиды.

Из выражения для спектральной плотности легко получить формулы для вычисления амплитудного и фазового спектров:

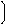
Расчёты показывают, что амплитудный спектр в данном случае имеет такой же вид, как и в предыдущем, когда выборки u(0)=0, 5; u(Т_д)=0, 866; u(2Т_д)=-0, 5; u(3Т_д)=-0, 866.

Фазовый спектр имеет иной вид: у него ещё более нелинейный характер со скачкообразным изменением фазы от -p/2 до +p/2 в узлах, определяемых нулевым и кратными целым чётным значениям текущей частоты w (рис. 2. 21).

Рис. 2. 21. Фазовый спектр одного периода синусоиды при u(0)=0, 866;

u(Т_д)=0, 5; u(2Т_д)=-0, 866; u(3Т_д)=-0, 5

Оценим предел эволюции комплексной величины S_д(jw). Пусть " нулевая" выборка u(0)=1, т. е. w₁t+y_u=p/2; остальные три выборки – u(Т_д)=0; u(2Т_д)=-1; u(3Т_д)=0. Тогда формула для определения спектральной плотности принимает вид

Годограф комплексной величины S_д(jw) в рассматриваемом случае в диапазоне изменения кратности 0£ q£ 2 имеет форму правильной окружности, симметрично размещённой относительно оси абсцисс в 1-м и 4-м квадрантах (рис. 2. 22): значению q=0 соответствует нулевой вектор S _д(0)=0× e^j^p^/², а q=1 – вектор S _д(w₁)=2 (на верхней половине годографа точкой отмечено положение конца вектора при q=0, 5), значению q=2 – S _д(w₂)=0× e^-^j^p^/² (на нижней половине годографа точкой отмечено положение конца вектора при q=1, 5). В диапазоне 2£ q£ 4 и других годограф имеет такую же форму.

Рис. 2. 22. Функция S_д(jw) периода

синусоиды при u(0)=1; u(Т_д)=0; u(2Т_д)=-1; u(3Т_д)=0

Из выражения для спектральной плотности следует, что модуль и фазу комплексной величины S_д(jw) можно вычислить по формулам

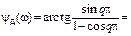
Амплитудный спектр описывается таким же выражением, как и в случае, когда u(Т_д)=u(2Т_д)=0, u(Т_д)=1, u(3Т_д)=-1 и две выборки попадают на экстремумы синусоиды. Выборки производятся в моменты времени так, что u(0)=1, u(Т_д)=0, u(2Т_д)=-1 и u(3Т_д)=0. Амплитудный спектр, естественно, имеет точно такой же вид, как и на рис. 2. 17. Фазовый спектр имеет линейный характер со скачкообразным изменением фазы от -p/2 до +p/2 в узлах, определяемых нулевым и целыми чётными значениями кратности: q=0, ±2, ±4…; скачки фазы не превышают p (рис. 2. 23).

Рис. 2. 23. Амплитудный и фазовый спектры одного периода синусоиды

при u(0)=1; u(Т_д)=0; u(2Т_д)=-1; u(3Т_д)=0

Пример 2. 7. Импульс напряжения, имеющий вид одного периода синусоиды единичной амплитуды частоты 50Гц – u(t)=sin(w₁t+y_u), дискретизирован шестью выборками; первая осуществляется в момент t=(p/6-y_u)/w₁. Найти спектр дискретизированного сигнала.

Для определения спектра воспользуемся формулой (2. 41), которая при N=6 принимает вид

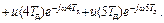
Интервал дискретизации Т_д=3, 333 мс (w_д=1884с^-¹), т. е. один период синусоиды будет представлен шестью отсчётами: u(0)=0, 5; u(Т_д)=1; u(2Т_д)=0, 5; u(3Т_д)=-0, 5; u(4Т_д)=-1; u(5Т_д)=-0, 5. Тогда спектральная плотность, вычисленная в соответствии со значением периода дискретизации

где ;

Годограф комплексной величины S_д(jw) в диапазоне изменения кратности 0£ q£ 3 расположен во всех четырёх квадрантах (рис. 2. 24):

Рис. 2. 24. Спектральная плотность одиночного периода синусоиды при

u(0)=u(2Т_д)=0, 5; u(Т_д)=1; u(3Т_д)=u(5Т_д)=-0, 5; u(4Т_д)=-1

значениям q=0, q=1 и q=3 соответствуют векторы S _д(0)=0× e^j^p^/², S _д(w₁)=3e^-^j^p^/³ и S _д(w₃)=0× e^j^p (на годографе точками отмечено положение конца вектора при q=0, 6; q=1, 8 и q=2).

В диапазоне 3£ q£ 6 годограф имеет зеркально отражённую форму: значению q=4 соответствует вектор S _д(w₄)=0× e^-^j^p^/², а q=5 – вектор S _д(w₅)=3e^j^p^/³ (на кривой годографа точками отмечено положение конца вектора при q=4, 2; q=5, 4 и q=6). Указанный диапазон изменения кратности q соответствует полному циклу изменения спектральной плотности одиночного периода дискретизированной синусоиды, если N=6.

Из выражения для S_д(jw) легко получаются формулы для вычисления амплитудного и фазового спектров:

При N=6 амплитудный спектр дискретизированного сигнала (рис. 2. 25) уже существенно ближе амплитудному спектру аналогового (рис. 2. 5, б).

Фазовый спектр имеет линейный, но более сложный характер со скачкообразным изменением фазы от -p/2 до +p/2 только в узлах, определяемых нулевым и целыми чётными значениями q, кратными N (q=0, ±6, ±12, …). Во всех узлах, определяемых целыми

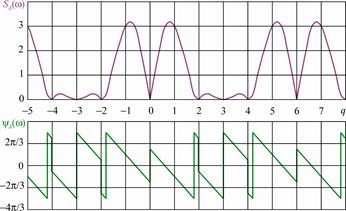
Рис. 2. 25. Амплитудный и фазовый спектры одиночного периода синусоиды

при u(0)=u(2Т_д)=0, 5; u(Т_д)=1; u(3Т_д)=u(5Т_д)=-0, 5; u(4Т_д)=-1

чётными значениями q=2±N, скачок фазы такой же, но от 5p/6 до -p/6, а в узлах q=4±N он тоже равен p, но скачок y(w) происходит от p/6 до -5p/6. В узлах, кратность которых не равна целому числу, – q=±1, 8; ±4, 2; ±7, 8; ±10, 2 и т. д. – скачок фазы максимален – равен 2p.

Оба спектра имеют периодический характер с частотой повторения ±w_д=1884с^-¹.

⇐ Предыдущая 1 2 3 4 567 Следующая ⇒

Воспользуйтесь поиском по сайту: