После подстановки выражения (2.25) в соотношение (2.23) имеем

 

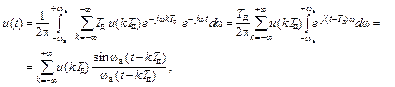
что и требовалось доказать.

Простейшие сигналы вида

 

s_k(t)=                                                             (2. 26)

 

называются функциями отсчётов (рис. 2. 11) или базисными функциями Котельникова.

Рис. 2. 11. Функции отсчётов

Имеющий длительность t_к и верхнюю граничную частоту спектра f_в, может быть представлен ограниченным рядом Котельникова:

,                                            (2. 27)

 

где N=t_к/Т_д – число отсчётов за интервал времени, равный длительности импульсного сигнала t_к.

Пример 2. 6. Представить рядом Котельникова один период синусоиды u(t)=sin(w₁t+y_u) частоты 50Гц (t_к=Т₁=20мс) единичной амплитуды, дискретизированный четырьмя равноотстоящими выборками, первая из которых осуществляется в момент t=-y_u/w₁ (рис. 2. 12, а).

При выборе интервала дискретизации синусоидального сигнала из условия Т_д£ 0, 5/f_в (f_в=w_в/2p – верхняя граничная частота спектра) аналоговый сигнал u(t) можно однозначно восстановить по его отсчётам:

 

u_к(t)=sin kp +y_u.

 

Интервал дискретизации Т_д=0, 25Т₁=5мс, следовательно, импульс синусоидальной формы будет представлен двумя отсчётами, поскольку u_к(0)=0, u_к(2Т_д)=0. Тогда в соответствии с формулой (2. 27) после замены частоты w_в на p/Т_д математическая модель аппроксимирующей функции

 

 

где t_д*=t/T_д.

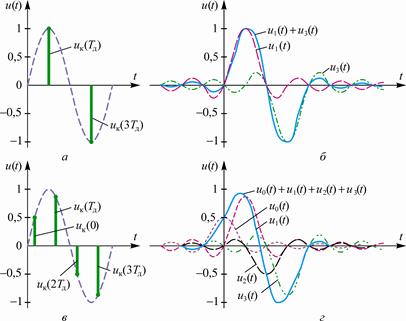
Графики аппроксимирующей функции u_S(t)=u₁(t)+u₂(t) и отдельных её слагаемых u₁(t) и u₂(t) показаны на рис. 2. 12, б. Эти графики показывают довольно близкое соответствие сигнала u(t) и отображающей его кривой u_S(t) (имеется в виду общий характер, а не мгновенные значения сравниваемых сигналов, которые не только в двух временных диапазонах -¥ < t£ 0 и T₁³ t> ¥, но даже и в интервале 0< t< T₁ существенно отличаются друг от друга).

Выборки могут и не попадать на нулевые значения синусоиды, тогда они не будут попадать и на экстремумы, но общее число членов ряда Котельникова при этом будет в 2 раза больше, так как u_к(0)¹ 0, u_к(2Т_д)¹ 0. Можно предположить, что точность аппроксимации исходного сигнала от увеличения числа членов ряда Котельникова только повысится.

Пусть " нулевая" выборка u_к(0)=0, 5 (w₁t+y_u=p/3), остальные три выборки – u_к(Т_д)=0, 866; u_к(2Т_д)=-0, 5; u_к(3Т_д)=-0, 866. С учётом указанных выше замен в (2. 27) математическая модель аппроксимирующей функции примет следующий вид:

 

 

Графики функции u_S(t)=u₀(t)+u₁(t)+u₂(t)+u₃(t) и отдельных её слагаемых u₀(t), u₁(t), u₂(t) и u₃(t) показаны на рис. 2. 12, г. Они показывают бó льшее расхождение сигнала u(t) и отображающей его кривой u_S(t) по сравнению с предыдущим случаем. Это объясняется существенным отличием базисной функции S₀(t), положительная полуволна которой располагается между значениями -Т_д=-5мс и +Т_д=5мс относительно момента Т_д=0, в интервале значений левее момента t=-3, 33мс, когда функция u(t) переходит через нуль. *

Увеличение числа членов ряда Котельникова при неизменном значении N не увеличило точность аппроксимации, причиной чего являются моменты взятия отсчётов. Можно показать, что самая высокая точность аппроксимации синусоидального сигнала будет тогда, когда выборки " попадают" на её экстремумы, как это показано на рис. 2. 12, б. Причём это будет справедливым даже при N=2. Однако, если обе выборки будут производиться в окрестностях точек перехода синусоиды через нуль, то после восстановления сигнала по этим выборкам аппроксимирующая кривая будет весьма далека от реального сигнала.

*		Базисная функция Котельникова S0(t) определяет значения функции u0(t)=0, 5S0(t) на всём протяжении рассматриваемого изменения t.

 

Рис. 2. 12. Апериодический сигнал и его аппроксимирующая функция:

            а – u_к(0)=0, u_к(Т_д)=1, u_к(2Т_д)=0, u_к(3Т_д)=-1;

            б – кривая u_S(t), вычисленная по двум выборкам;

            в – u_к(0)=0, 5; u_к(Т_д)=0, 866; u_к(2Т_д)=-0, 5; u_к(3Т_д)=-0, 866;

            г – кривая u_S(t), вычисленная по четырём выборкам

 

Таким образом, при суммировании членов ряда Котельникова (2. 27) в любые отсчётные моменты времени kТ_д непрерывный сигнал точно аппроксимируется независимо от числа отсчётов. В интервале между двумя соседними отсчётами сигнал u(t) аппроксимируется тем точнее, чем больше суммируется членов ряда.

Если амплитудные отсчёты производятся с недостаточной частотой и условия теоремы Котельникова нарушаются, то однозначная аппроксимация исходного сигнала принципиально невозможна, поскольку через отсчётные моменты можно провести множество кривых, спектральная плотность которых отлична от нуля вне полосы частот -f_в £ f £ f_в.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: