 |
где tk=kT1=2kp/w1; T1 – период; k – целое число периодов за интервал tk.
|
|
|
|
На основании выражения (2. 17)
.
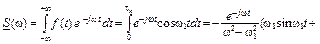
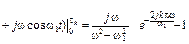Отсюда получаются формулы для вычисления амплитудного и фазового спектров:
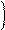
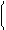
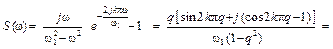
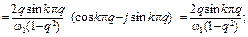
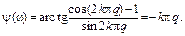
Модуль комплексной величины S(jw) на основной частоте вычисляется также по правилу Лопиталя:
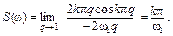
Спектральная плотность S(jw) отображается в комплексной плоскости годографом, который описывает конец вектора S (w) при изменении w в области положительных значений (рис. 2. 7, б).
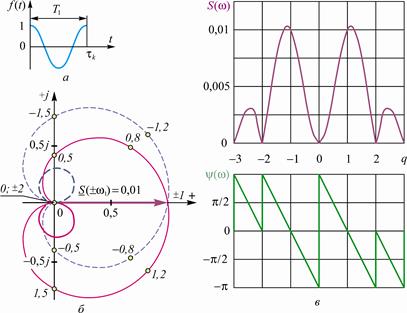
Рис. 2. 7. Спектральные характеристики апериодической косинусоиды:
а – один период косинусоиды; б – его спектральная плотность;
в – амплитудный и фазовый спектры
Этот годограф в диапазоне изменения кратности 0£ q£ 2 имеет форму " яблока", асимметрично размещённого в четырёх квадрантах: в диапазоне изменения кратности 0£ q£ 2 значению q=0 соответствует векторная величина S (0) =0× ejp/2, значению q=1 – S (w1)=0, 01, а значению q=2 – S (w2)=0× e-jp (на кривой годографа точками отмечены значения q=0, 5; 0, 8; 1, 2; 1, 5). В диапазоне 2£ q£ ¥ годограф приобретает вид спирали, размещённой в нижней полуплоскости и сворачивающейся к началу координат; значениям q=2, 3, …соответствуют векторы c нулевым модулем: S (w2+)=S (w3+)=S (w4+)=…=0, S (w2-)=S (w3-)=S (w4-)=…=0× e-jp (здесь частота wx+ соответствуют правому пределу частотного диапазона, а wx- – левому).
Спектральную плотность S(jw) для отрицательных значений w отображает годограф вектора S (-w) – штриховая линия на рис. 2. 7, б. Этот годограф относительно оси абсцисс расположен симметрично годографу, определяемому положительными значениями w, что обусловливает симметричное расположение амплитудного спектра S(w) относительно частоты w=0 (рис. 2. 7, в).
|
|
|
Фазовый спектр имеет линейный характер со скачкообразным изменением фазы от -p до +p на нулевой частоте, при q=±1 фаза y(±w1)=0. Особенностью фазового спектра являются скачки фазы, равные p, в узлах, определяемых значениями кратности, равными q=±2, ±3, ±4, …, но в области отрицательных значений q фаза изменяется от p до 0, а в области положительных значений q – от 0 до -p.
С увеличением k (рис. 2. 8, а) отображение S(jw) в комплексной плоскости принимает более сложный вид (рис. 2. 8, б): при 0£ q£ 0, 5 конец вектора S (w) вначале описывает размещённую в верхней полуплоскости окружность неправильной формы. Когда 0, 5£ q£ 1, 5, годограф имеет форму " яблока", размещённого асимметрично во всех квадрантах: значению q=0, 5 соответствует вектор S (w0, 5)=0× ejp, значению q=1 – S (w1)=0, 02, а значению q=1, 5 – S (01, 5)=0× e-jp (на годографе точками отмечены значения q, равные 0, 75; 0, 9; 1, 1; 1, 25). В диапазоне 1, 5£ q£ ¥ годограф приобретает вид спирали, размещённой в нижней полуплоскости и стремящейся к началу координат; значениям q=2; 3; … соответствуют нулевые векторы S (w2)=S (w3)=…=0, а значениям q=2, 5; 3, 5 … – векторы с модулем, равным нулю, но с фазовым углом, равным -p: S (w2, 5)=S (w3, 5)=…=0× e-jp.
Амплитудный спектр S(w) симметричен относительно частоты w=0, а нулевые значения S(w) имеются не только в узлах с нулевым и целыми значениями q, но и в узлах со значениями q=±0, 5; ±1, 5; ±2, 5; … (рис. 2. 8, в).
Фазовый спектр имеет линейный характер со скачкообразным изменением фазы от -p до 0 в узлах, определяемых значениями q=1, 5; 2; 2, 5; 3; 3, 5; …, и от p до 0 в узлах, определяемых
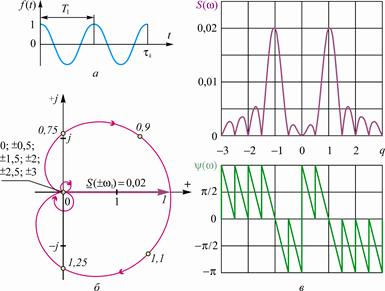
Рис. 2. 8. Спектральные характеристики апериодической косинусоиды:
а – два периода косинусоиды; б – их спектральная плотность;
в – амплитудный и фазовый спектры
значениями q=±1, 5; ±2; ±2, 5; … Если q=0, 5, имеется скачок фазы от 0 до p; если q=-0, 5 – от 0 до -p. При q=±1 фаза y(w1)=0. Скачок фазы, равный 2p, наблюдается только при q=0.
|
|
|
Сопоставление графиков амплитудных спектров одного и двух периодов косинусоиды показывает, что по мере увеличения k амплитудный спектр так же, как и в предыдущем примере, концентрируется во всё более узком частотном диапазоне в областях, примыкающих к значению основной гармоники w1 и её " зеркальному" соответствию -w1. Так, при k=2 наибольшее значение S(w) достигается на частотах ±w1 (рис. 2. 8, в) и оно в 2 раза больше, чем при k=1 (рис. 2. 7, в), но уже на частотах w±0, 5=±0, 5w1 и w±1, 5=±1, 5w1 модуль S(w)=0. При k®¥ составляющая амплитудного спектра S(w1) стремится к бесконечности, это соответствует дискретному спектру непрерывной косинусоиды с конечным значением амплитуды на основной частоте.
|
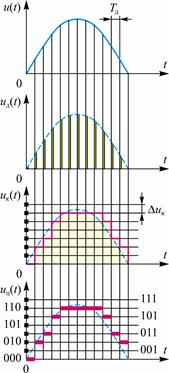
Рис. 2. 9. Аналого-цифровое преобразование сигнала |
Аналого-цифровое преобразование входных сигналов
Преобразование аналогового сигнала в цифровой сопряжено с необходимостью выполнения трёх операций: дискретизацией по времени, квантованием по уровню, формированием кодов (кодированием) (рис. 2. 9).
Теорема Котельникова.
Аналитически теорема Котельникова представляется рядом
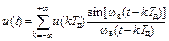. (2. 20)
где k – номер отсчёта; u(kTд) – значения аналогового сигнала в точках отсчёта; wв=2pfв – значение верхней круговой частоты спектра сигнала.
Непрерывный сигнал u(t) имеет сосредоточенную в полосе частот –wв£ w£ wв спектральную плотность S(w) (рис. 2. 10). Если спектральную плотность S(w) симметрично клонировать с периодом 2wв (штриховые линии на рис. 2. 10) и полученную " периодическую" функцию разложить в ряд Фурье в
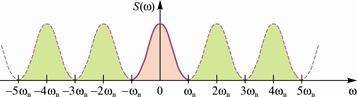
Рис. 2. 10. Периодическое представление амплитудного спектра функции u(t)
комплексной форме, заменив в формуле (2. 7) аргумент t на w, частоту w1=wв на Tд и q на k, то
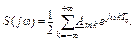(2. 21)
Тогда в формуле вычисления комплексных коэффициентов (2. 8) период равен 2wв, а интервал дискретизации Tд=p/wв, следовательно:
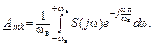(2. 22)
По формуле обратного преобразования Фурье (2. 19) исходный сигнал представляется в следующем виде:
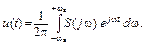(2. 23)
|
|
|
Значение дискретизированного сигнала для k-го отсчёта времени с учётом того, что t=kTд=kp/wв:
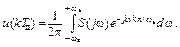(2. 24)
Из выражений (2. 22) и (2. 24) следует, что A mk=2Tдu(-kTд). С учётом этого выражение (2. 21) для спектральной плотности сигнала принимает вид:
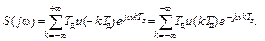(2. 25)
|
|
|
