 |
Спектры апериодических функций
|
|
|
|
Спектры апериодических функций
Если обозначить wq=qω 1, то ряды Фурье (2. 7) и (2. 8) запишутся как
 (2. 12)
(2. 12)
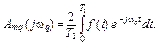 (2. 13)
(2. 13)
для спектра периодической последовательности прямоугольных импульсов


 . (2. 14)
. (2. 14)
Коэффициенты амплитудного спектра сигнала из примера, рассмотренного выше, для разных значений периода T1
Таблица 2. 1
| q | Т1, мс | |||||||||||
| |А mq| | 0, 25 | 0, 225 | 0, 159 | 0, 075 | 0, 045 | 0, 053 | 0, 032 | 0, 025 | 0, 032 | |||
| 0, 1 | 0, 098 | 0, 094 | 0, 086 | 0, 076 | 0, 064 | 0, 05 | 0, 037 | 0, 023 | 0, 011 |
Спектральная функция или спектральная плотность:
 (2. 15)
(2. 15)
Спектральная плотность пропорциональна отношению амплитуд спектра к основной частоте:
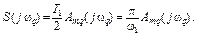 (2. 16)
(2. 16)
При T1®¥ дискретная частота обращается в непрерывную частоту wq=qω 1®¥, а спектральная плотность (2. 15) – в непрерывную функцию ( прямое преобразование Фурье ):
 (2. 17)
(2. 17)
Для существования интеграла (2. 17) временнá я функция должна удовлетворять условию абсолютной интегрируемости:
 < ¥.
< ¥.
Пример 2. 3. Определить спектральную плотность прямоугольного импульса единичной амплитуды и длительности tи (рис. 2. 4, а).
В одиночный прямоугольный импульс может быть преобразована периодическая последовательность единичных прямоугольных импульсов (рис. 2. 3) посредством предельного увеличения периода их повторяемости: Т1®¥. Тогда, при wq=ω, из выражений (2. 14) и (2. 16)
|
|
|
|
Рис. 2. 4. Единичный прямоугольный импульс и его спектры |
 ,
,
т. е. спектральная плотность единичного импульса является вещественной и чётно-сим-метричной функцией (рис. 2. 4). Отрицательные значения S(jw) обусловлены соответствующим знаком периодической функции sinx. Непрерывный фазовый спектр с изменением знака функции sinx в каждом узле изменяет фазу y(w) на p: если w> 0, то y(w)=p, если w< 0, то y(w)=-p.
Непрерывная комплексная спектральная функция ‒ это комплексная функция вещественной частоты, которая может быть выражена через действительную и мнимую составляющие:
 ,
,
где S(w), y(w) – модуль и фаза спектральной функции, называемые непрерывными амплитудным и фазовым спектрами.
Эти соотношения показывают связь между рядом Фурье периодической временнó й функции, представляемой дискретным спектром, и преобразованием Фурье апериодического сигнала в виде одного периода периодической функции, представляемого непрерывным спектром.
Для получения комплексных коэффициентов ряда, определяющих дискретный спектр, достаточно значения спектральной плотности в дискретных точках wq=qω 1 умножить на 2/T1=ω 1/p:

 .
.
Следовательно, имея дискретный спектр периодического сигнала, после его умножения на ω 1/p можно получить значения спектральной плотности сигнала в виде первого периода в дискретных точках qω 1.
В процессе предельного преобразования частоту ω 1 можно рассматривать как равное D(qω 1)=Dwq=Dw=ω 1 приращение переменной, за каковую принимается частота. Тогда ряд Фурье (2. 12) с учётом выражения (2. 15) приобретает следующий вид:
 (2. 18)
(2. 18)
В пределе Т1®¥, тогда приращение D(qω 1)=Dw превращается в дифференциал dw, а процесс суммирования по выражению (2. 18) – в интегрирование, называемое по аналогии с интегралом (2. 17) обратным преобразованием Фурье:
|
|
|
 (2. 19)
(2. 19)
Обратное преобразование Фурье всегда является двухсторонним, т. к. суммируются сопряжённые гармоники.
Пример 2. 4. Найти спектральную плотность отрезка синусоиды единичной амплитуды частоты 50Гц, включающего один период (рис. 2. 5, а):

где tk=kT1=2kp/w1; T1 – период; k – целое число периодов за ин-тервал tk.
На основании выражения (2. 17)
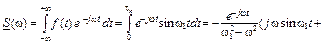


 .
.
Отсюда получаются формулы для вычисления амплитудного и фазового спектров:









|
|
|



