7.2. Определение размера блоков мозаики

7. 2. Определение размера блоков мозаики

и величины микронапряжений по ширине линий

Метод изучения истинной ширины и формы рентгеновских линий позволяет определить в образце размер блоков мозаики D, величину микронапряжений иплотность дислокаций.

Величину микронапряжений характеризуют средним относительным отклонением параметров решетки от ихосновного значения ∆ а/а. Источниками их являются несовершенства кристалличесиого строения дислокации, точечные дефекты и их скопления, и т. д. Микроискажения в металлических порошках могут возникать в результате пластической деформации при получении ихмеханическим диспергированием (растиранием, размолом, фрезерованием ит. д. ), при охлаждении плакированных (покрытых другим металлом) порошков в результате отличия коэффициентов линейного расширения контактирующих металлов, при выделении изыточпой фазы (старении) в порошках из легированных металлов и сплавов, в процессе образования металлических частиц из неметаллических фаз и т. д. Микронапряжения в порошках, возникают также в процессе дальнейшего их компактирования путем прессования, прокатки и т. д. и даже при спекании порошков, если система гетерофазна [3] или материал имеет коэффициент линейного расширения, сильно  отличающийся  в разных кристаллографических направлениях.

Экспериментально и теоретически показано, что измельчение порошковых частиц до 100-1500 А или блоков мозаики в более крупных частицах до этих же пределов вызывает уширение рентгеновских линий. Размытие линий вызывает также и наличие микроискажений кристаллической решетки. Влияние каждого из этих факторов на профиль размытой линии различно. Поэтому, анализируя профиль линии, можно установить причину размытия

и количественно определить величину блоков мозаики и микро­искажений, вызвавших его размытие, т. е. определить параметры тонкой кристаллической структуры [4-8]. Вопросы  методики

определения этих характеристик актуальны до настоящего времени [14-21].

Имеется два основных метода рентгенографического изучения тонкой кристаллической структуры порошков и поликристаллических образцов [14]: 1) интегральный метод, или метод аппроксимации, основой которого является ширина (полуширина) линии;

2)

f

метод гармонического анализа, экспериментальной основой которого является профиль рентгеновской  интерференционной

линии.

Метод аппроксимации. Основной задачей метода аппроксимации является правильное выделение физического уширения из общей ширины линии образца [4 6, 8]. Известно, что, кроме физических факторов

(измельчения блоков и наличия микронапряжений), на ширину рентгеновских линий влияет спектральная неоднородность используемого характеристического рентгеновского излучения

-0

Рис. 7. 2. Сравнительный видрентгеновских максимумов эталона (1) и исследуемого образца (2)

(существование α -дублета)  и  геометрия                      съемки,   которая определяет инструментальную ширину линии.  Выделить   α линию  из                                                      α -дублета можно специальными приемами, а за инструментальную ширину принять исправленную на дублетность ширину линии эталона, т. е. образца из того же вещества, но свободного от микроискажений  и  имеющего                                           крупные  блоки (> 0, 15 мкм) (рис. 7. 2). Так как изготовить совершенный эталон довольно трудно, то пользоваться эталоном рекомендуют в случае больших уширений. Если же состояние образца близко к равноному, то несовершенство эталона может внести заметную погрешность в конечные результаты, и тогда инструментальную

шиирину следует определять расчетным путем [14], точно и полно учитывая всю геометрию съемки.

Расчет физического (дифракционного) уширения β по исправленной на дублетность ширине линии образца В и ее инструментальной ширине b имеет ряд особенностей, так как дифракционная иинструментальная ширина не являются аддитивными. Каждый элемент инструментальной ширины испытывает дифракционное размытие независимо, ирезультирующая размытая линия получается путем наложения размытых линий, образуемых всеми элементами исходной инструментальной ширины [10].

Точное соотношение между β, В и b можно выразить уравнением:

 

 

(7. 7)

 

где g(х) - функция, описывающая угловое распределение интенсивности за счет геометрии съемки (линия эталона); f(х) - соответствующая функция для одновременного действия геометрbb съемки ифизического уширения (линия образца). Во многих случаях такое распределение можно аппроксимировать (отсюда иназвание метода) одной из гладких функций: e^-ax2(распределенпе Гаусса), 1/(1+α x²)(распределение Коши)  и

1/(1+α x²⁾  (промежуточное распределение). Решения уравнения (7. 7) с подстановкой одинаковых распределений для функций f(x) и g(x) дают β =B-b(распределение Коши);

β =½ (B-b+ 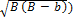 (промежуточное распределение)

β = 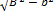 (распределение Гаусса).

Найденное таким способом истинное физическое уширение может быть пересчитано на размер блоков, величину микронапряжений и плотность дислокаций.

Экспериментальная процедура получения профиля рентгеновских линий образца и эталона та же, что и в методе экстинкцип. Чаще всего на каждой дифрактограмме выбирают две линии: одну с малым значением суммы квадратов индексов, другую с большим. Чтобы избежать ошибок, вызванных неравноосностью блоков, обе линии должны принадлежать одной отражающей плоскости в разных порядках отражения [14]. Выбор пары линий и длины волны рентгеновского излучения для достижения максимальной точности описан в [14]. В другом варианте проводят промер всех линий, присутствующих на дифрактограмме [2, 22].

Обработка экспериментальных данных проводится следующим образом. Вначале исправляют искажение линий за счет а-дублета, выделяя α ₁-компоненту Экспериментально полученная кривая представляет собой наложение двух независимых α ₁ и α ₂ кривых, расстояние между которыми увеличивается с ростом угла отра­ жения θ. Искажение линии в области малых углов отражения исправляют, пользуясь графиком поправок на а-дублет для разных аппроксимирующих функций [8, 23].

. В области больших углов, где дублет разрешается, проводят графическое разделение α ₁и α ₂-компонент методом Решингера [4, 8] или для убыстрения используют специальный шаблон [24], основанный на том же принципе. Предложен также аналитический метод разделения дублета, позволяющий автоматизировать этот процесс [25]. Интегральную ширину линии определяют как отношение площади, ограниченной профилем линии и фоном, к максимальной высоте линии и выражают в радианах.

Пригодность той или другой аппроксимирующей функций можно проверить, строя графики в выпрямляющих координатах:

Ln y=f(x²) для функции е^-ax2, 1/y-1 = f(x²)для  функцип

1/(1+α x²) и 1/ 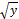-1=f(x²) для функции 1/(1+α x²)²  где x и y - значения абсцисс и ординат проверяемого профиля линии в любых линейных единицах. Лучшей аппроксимирующей функцией будет такая для которой график, построенный в спрямляющих

осях, будет ближе к прямой. Для металлов с кубической структурой функций f(х) и g(х) аппроксимируются_с достаточной степенью приближения функцией 1/(1+α x²)² [8].

Когда аппроксимирующая функция выбрана, физическое уширение β определяют по приведенным выше формулам. Если из условий эксперимента заведомо известно, что истинное физическое уширение вызвано или исключительно микроискажениями, или только измельчением блоков мозаики, то величина искажений решетки в направлении, перпендикулярном плоскости отражения, как и размер блоков в этом направлении, вычисляются по формулам (7. 9), (7. 10)

Когда в изучаемом образце уширение линий вызвано одновременным влиянием микроискажений и мелкодисперсности, то соответствующая доля их т и n в уширении находится графо-аналитическим расчетом, построенным на предположении о виде функций того и другого факторов и зависимости их от угла отражения θ. Расчет для случая измерений по паре линий подробно описан в [8, 26]. Искомые величины находятся по формулам:

Для кубической решетки, которую имеет большинство металлов, ∆ а/a=∆ d/d, где d -межплоскостное расстояние для данной кристаллографической плоскости HKL.

При использовании для расчета всех линий на рентгенограмме применяют иной способ разделения эффектов микроискажения и измельчения блоков, основанный на различной зависимости их от угла отражения θ и связи уширения за счет блоков с длиной волны λ рентгеновского излучения [14, 22]. Эта зависимость может быть выражена уравнением (7. 11)

 Величины β ²cos²θ /λ ² и 16sin²θ /λ ² используют  в качестве  переменных и строят прямую, угол наклона которой определяет величину микронапряжений ∆ а/а, а отрезок на оси ординат - величину 1/D2 [14].

В последнем случае, когда измерения ведутся по отражениям от различных кристаллографических плоскостей, нужно учитывать, что при наличии анизотропии модуля Юнга микроискажения Могут существенно различаться по величине для разных кристаллографических направлений [14], и это необходимо принимать во внимание при расчетах ∆ а/а для каждой кристаллографической плоскости [2].

Физическое уширение β дает такую физическую характеристику исследуемого материала, как плотность дислокаций, т. е. число линий дислокаций, пересекающих единицу площади. Плотность дислокаций рассчитывается по формуле [23]

Ρ =Аβ ²                                                                                                          (7. 12)

где А - коэффициент, зависящий от упругих свойств материала, вектора Бюргерса и других, а для металлов с кубической решеткой приблизительно равный 2*1016 см-2 

Если известны значения величины микроискожений ∆ а/а = ε

и блоков  D,  то  для  определения  средней  плотности  дислокаций используют  соотошение:

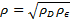                                                                                                (7. 13)

где ρ _D = 3/D2, ρ _ε = 16 ε 2 /b2 иb - вектор Бюргерса [23].

Как видно из изложения, метод аппроксимации доступен и достаточно прост. Был предложен вариант использования мини­ ЭВМ для обработки результатов этим методом, сокращающий время расчета примерно в 10 раз [1]. Однако применение метода аппроксимации связано с некоторыми допущениями, что ограничивает точность получаемых результатов, а неправильный подход к условиям эксперимента может привести к значительным ошибкам.

В настоящее время предложены математические методы, которые можно рассматривать как второе приближение метода аппроксимации [27-31]. Преимущество этих методов заключается в большей точности ивозможности получения реального распределения интенсивности исследуемых интерференционных линий. Получаемые результаты близки к данным  гармонического анализа. В то же время предлагаемые методики позволяют значительно сократить объем экспериментальной ивычислительной работы по сравнению с гармоническим анализом.

Метод гармонического анализа. Метод гармонического анализа профиля интерференционных линий нуждается в меньшем числе допущений, чем метод аппроксимаций, ипозволяет выделить кривую дифракционного уширения без каких-либо предположений о виде функции, описывающей контур линии. С помощью Фурье-анализа можно определить не только величину кристаллитов, но и статистику их распределения по размерам [10]. Однако этот метод требует более громоздкой и кропотливой обработки экспериментальных данных: прецизионного построения профиля

линии, машинной обработки результатов эксперимента [32-37]. Процедура     экспериментального    получения                       профиля                            линий та же, что и в методе аппроксимации, но регистрацию линий: следует проводить только с помощью дифрактометра в режиме записи по точкам, щель на счетчике уменьшить до 0, 1 мм, а шаг сканирования снизить до 0, 01°, так как точность гармонического анализа зависит от точности измерения профиля интерференцион­ ных линий. Очень важно также правильно провести линию фона

на дифрактограмме. В ряде работ показано, что завышения линий фона на 10% при выделении профиля линии практически не позволяет по коэффициентам Фурье установить причину уширения линий [5]. Для получения хорошей точности важно иметь малую инструментальную ширину линий, чему способствует использование острофокусных трубок [38]. Измерения профиля линий ведутся на исследуемом образце и эталоне.

Распределение интенсивности, зависящее от физических факторов f(х), можно выделить из экспериментального распределения интенсивности образца h(х), исключив распределение, обусловленное геометрическими факторами g(х), полученное с помощью эталона. Кривая физического уширения разбивается на элементы с основанием dy и высотой f(у). Каждая элементарная площадка кривой f(у) испытывает размытие за счет геометрических факторов. Экспериментальная кривая h(х) представляет собой наложение множества таких размытых элементов:

 

Для нахождения f(х) используют разложение в ряды Фурье кри­ вых h(х) и g(х), заменяя интеграл суммой членов этого ряда. Интервал разложения выбирается так, чтобы на концах иза его пределами функции h (х) и g (х) обращались в нуль.

Для практического определения коэффициентов Фурье-разложения существуют разные приемы имеханизированные устройства, но с появлением ЭВМ обработку экспериментальных результатов ведут на машинах, разрабатывая или используя уже известные программы [32-37].

По вычисленным коэффициентам разложения в ряд Фурье устанавливают причину размытия линий и производят раздельное определение дисперсности блоков и величины микронапряжений, а также других характеристик тонкой структуры [4, 8]. Предельная точность гармонического анализа ограничивается уширением, связанным с собственной шириной спектральной линии характеристического излучения. Анализ этого эффекта показывает, что методом гармонического анализа можно определять размер блоков до 10^-3 – 1, 5-10^-3 см имикроискажения, превышающие 4*10^-4 [14].

К настоящему времени имеется много работ по применению анализа профиля рентгеновских линий к проблемам порошковой металлургии. Этим методом проводят изучение тонкой кристаллической структуры исходных металлических порошков, а также изменений тонкой структуры, происходящих на всех этапах получения спеченных материалов.

Прессование приводит к изменению тонкой структуры порошков. С увеличением давления прессования наблюдаются рост микроискажений, измельчение блоков и увеличение плотности дислокаций

Степень упрочнения прессовок находится в прямой зависимости от характеристик тонкой структуры [1, 40-48].

Зависимость микрjтвердости спеченных изделий из порошков от тонкой структуры позволяет перейти непосредственно к   расчету прочности спеченных материалов как функции изменения параметров тонкий структуры и физико-химич: еских факторов в процессе прессования испекания [40].

Зная среднюю плотность дислокаций в спеченном и деформированном порошковом теле, можно определить соотношение структурной и пластической компонент деформации при различных давлениях прессования [47].

Ширина рэнтгеновской интерференционной линии - очень чувствительный индикатор степени дефектности порошков. Она надежно отражает ход снятия деформационных искажений при рекристаллизации частиц порошка [40]. Установлено, что какую­ то часть искажений, вызывающих расширение линий спрессованных дисперсных порошков, следует отнести за счет дефектов, связанных с поверхностью частиц [49].

Следует упомянуть, что на расширение линий влияют также дефекты упаковки, которые необходимо учитывать при помощи анализа профиля интерференционного максимума [50, 51].

 

⇐ Предыдущая12131415161718192021Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: