 |
1.2 Критерии надежности невосстанавливаемых изделий
|
|
|
|
1. 2 Критерии надежности невосстанавливаемых изделий
Пусть на испытании находится N0 объектов, и пусть испытания считаются законченными, если все они отказали. Вместо отказавших образцов отремонтированные или новые не ставятся. В таких случаях критериями надежности изделий являются:
– вероятность безотказной работы P(t);
– частота отказов f(t);
– интенсивность отказов l(t);
– средняя наработка до отказа T1 (в некоторых источниках Tср).
Вероятностью безотказной работы (ВБР) называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени или в пределах заданной наработки не произойдет ни одного отказа.
Функция Р – относительная продолжительность непрерывной исправной работы объекта до первого отказа, а аргумент t – время, за которое нужно определить ВБР, следовательно, согласно определению,
P(t) = P(T ≥ t), t ≥ 0, (1. 1)
где T – время работы объекта от начала до первого отказа; t – время, в течение которого определяется вероятность безотказной работы.
|
P(t ) = (N 0 - n(t ))/ N 0, (1. 2)
где
P(t ) – статистическая оценка вероятности безотказной работы;
|
n(t) – число отказавших элементов за время t.
На практике, наряду с ВБР, определяют такую характеристику,
как вероятность отказа Q(t).
Вероятностью отказа называется количественная мера того, что при определенных условиях эксплуатации в заданном интервале времени возникает хотя бы один отказ.
|
|
|
Отказ и безотказная работа являются событиями несовместными и противоположными, поэтому при 0 £ t
Q (t ) = P (T < t ) ,
Q (t ) = 1- P (t ) = F (t ),
(1. 3)
где
Q (t ) = F (t )
– интегральная функция распределения случайной
величины.
Статистически вероятность отказа равна:
Ù
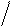 Q(t ) = n(t )
Q(t ) = n(t )
N0, (1. 4)
t / Dt
Ù å ni
Q(t) =
lim
Dt®0
i=1 ,
N 0
где ni – число неблагоприятных исходов;
N0 – общее число испытаний.
Если функция Q(t) дифференцируема, то производная от интегральной функции распределения – дифференциальный закон (плотность вероятности, плотность распределения) случайной величины Т – времени безотказной работы:
 f (t) = dQ(t) =
f (t) = dQ(t) =
dF (t) = - dP(t). (1. 5)
dt dt dt
Частотой отказов по статистическим данным называется отношение числа отказавших элементов в единицу времени к первоначальному числу работающих (испытываемых) при условии, что
все вышедшие из строя изделия не восстанавливаются. Согласно определению,
Ù
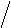
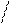 f (t) = n(Dt ) N0Dt или a(t) = n(Dt) N0Dt , (1. 6)
f (t) = n(Dt ) N0Dt или a(t) = n(Dt) N0Dt , (1. 6)
где n(Dt) – число отказавших элементов в интервале времени от
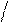
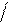 (t - Dt) 2 до (t + Dt) 2.
(t - Dt) 2 до (t + Dt) 2.
Частота отказов есть плотность вероятности (или закон распределения) времени работы изделия до первого отказа. Поэтому
f (t ) = - dP = -P¢ (t ) = dQ(t )Q¢ (t ),
dt dt
t
Q (t ) = ò f (t )dt , (1. 7)
|
f (t)dt . (1. 8)
|
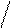 l(t) = n(Dt )
l(t) = n(Dt )
Ncp × Dt , (1. 9)
где N ср = (Ni + Ni+1)/2 – среднее число исправно работающих изделий
в интервале Dt ;
Ni – число изделий, исправно работающих в начале интервала Dt
|
|
|
Dt.
Ni+1 – число изделий, исправно работающих в конце интервала
Интенсивность отказов в вероятностной оценке есть условная
плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник.
Вероятностная оценка характеристики l(t) находится из выражения
l(t) = f(t) / P(t) (1. 10)
или f(t) = l (t) P(t).
Интенсивность отказов и вероятность безотказной работы связаны между собой зависимостью
| |
(1. 11)
Средней наработкой до первого отказа называется математическое ожидание времени работы объекта до отказа.
Математическое ожидание средней наработки до отказа T1 вычисляется через частоту отказов (плотность распределения времени безотказной работы):
+¥
mt = T1 = ò
-¥
tf (t)dt
(1. 12)
Зная, что t > 0 и P(0) = 1, а P(∞ ) = 0, определяют T1:
¥
T1 = ò P(t)dt
(1. 13)
Средняя наработка до первого отказа, согласно статистическим данным об отказах, вычисляется по формуле
Ù m
T1 = (å niti) / N 0, (1. 14)
i=1
где ti – время безотказной работы i-го образца;
N0 – число испытываемых объектов.
Для определения средней наработки до первого отказа
необходимо знать моменты выхода из строя всех испытываемых
Ù
объектов. Поэтому для вычисления T1 пользоваться данной формулой
неудобно. Имея данные о количестве вышедших из строя элементов ni в каждом i-м интервале времени, среднюю наработку до первого отказа лучше определять по уравнению
Ù m
T1 » (å nitcpi) / N0, (1. 15)
i=1
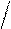
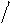 где tср и m находятся по следующим формулам:
где tср и m находятся по следующим формулам:
tср
= (ti-1 + ti ) 2,
m = tk
Dt , (1. 16)
где ti–1 – время начала i-го интервала;
ti – время конца i-го интервала;
tk– время, в течение которого вышли из строя все элементы;
Dt = ti-1 - ti – интервал времени.
При расчетах надежности технических устройств часто применяются законы распределения: экспоненциальный, усеченный нормальный, Рэлея, гамма, Вейбулла – Гнеденко, логарифмически- нормальный. В табл. 1. 1 приведены выражения для расчета количественных характеристик объектов, соответствующих перечисленным законам распределения времени их безотказной работы.
|
|
|













 Таблица 1. 1
Таблица 1. 1
Интенсивность отказов элементов
| Закон распределения | Частота отказов (плотность распределения) | Вероятност ь безотказной работы | Интенсивность отказов | Средняя наработка до первого отказа |
| Экспоненциаль ный | le-lt | e-lt | l = const | 1 l |
| Рэлея | - t 2 t e 2s 2 s 2 | - t2 e 2s 2 | t
 s 2
s 2
| ps |
| Гамма (при k целом) | e-l0t | e-l0t | l (l t )k -1 0 0 | k l0 |
| ( ) k -1 (l t )i k -1 ! å 0 i=0 i! | ||||
| Вейбулла – Гнеденко | k l ktk -1e-l0t | k e-l 0 t | l 0kt k -1 | Г ( 1 +1) k 1 l0 k |
| Усеченный нормальный | (t-T )2
1 e- 2s 2
F æ T1 ö s 2p
 ç ÷
è s ø
ç ÷
è s ø
| F æ T1 - t ö ç s ÷ è ø F æ T1 ö ç ÷ è s ø | (t-T )2 - e 2s 2 2ps F æ T1 - t ö ç s ÷ è ø | T12 T + s e- 2s 2 2p F æ T1 ö ç s ÷ è ø |
| Логарифми- чески- нормальный | 1æ ln t-m ö 2 1 - 2ç s ÷ s e è ø t 2p | 1 + Ф æ m - ln t ö 2 ç s ÷ è ø | 1æ ln t-m ö 2 ç ÷ 1 e2è s ø s t 2p 0, 5 + Ф æ m - ln t ö ç s ÷ è ø | 1 ¥ (ln t-m )2
 - dt
s p ò e 2
2 0
- dt
s p ò e 2
2 0
|




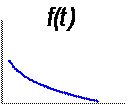
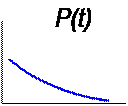
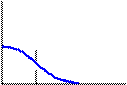
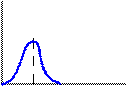
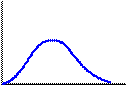
 Из приведенных соотношений видно, что все характеристики, кроме средней наработки до первого отказа, зависят от времени (являются функциями времени). На рис. 1. 2 показаны зависимости количественных характеристик надежности объектов от времени.
Из приведенных соотношений видно, что все характеристики, кроме средней наработки до первого отказа, зависят от времени (являются функциями времени). На рис. 1. 2 показаны зависимости количественных характеристик надежности объектов от времени.
 f P
f P
à )
t t t

 f
f
á )
t t t


 f P
f P
â )
 t
t
|
|
|
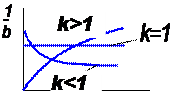 -1
-1
b
|
|
|
|
|
|
|
|



|
|
|
t t t

 f P
f P
å )
t t t
|
|
|
Рис. 1. 2 Зависимости количественных характеристик надежности от времени:
а – экспоненциальный закон; б – усеченный нормальный закон; в – закон Рэлея; г – гамма-распределение: д – закон Вейбулла – Гнеденко;
е – логарифмически-нормальный закон
Рассмотренные критерии надежности позволяют достаточно полно оценивать надежность невосстанавливаемых объектов, а также надежность восстанавливаемых объектов до первого отказа. Наличие нескольких критериев не означает, что всегда нужно оценивать надежность объектов по всем характеристикам.
Наиболее полной характеристикой надежности является частота отказов f(t) (плотность распределения), она содержит в себе все данные о случайном явлении – времени безотказной работы.
Средняя наработка до первого отказа является достаточно наглядной характеристикой надежности. Однако применение этого критерия для оценки надежности сложной системы ограничено в тех случаях, когда:
– время работы системы гораздо меньше среднего времени безотказной работы;
– закон распределения времени безотказной работы не однопараметрический и для достижения полной оценки требуются моменты высших порядков;
– система резервированная;
– интенсивность отказов не постоянная;
– время работы отдельных частей сложной системы разное.
Интенсивность отказа – наиболее удобная характеристика надежности простейших элементов, так как позволяет просто вычислять количественные характеристики надежности сложных систем.
Наиболее целесообразно оценивать надежность сложных систем по критерию вероятности безотказной работы, так как:
– она входит в качестве сомножителя в другие, более общие характеристики систем, например в эффективность и стоимость (цена и стоимость различаются);
– характеризует надежность с учетом изменения во времени;
– может быть получена сравнительно простыми расчетами в процессе проектирования систем и оценена в процессе испытаний.
|
|
|


