) = 2,5×10-5 × 0,98 = 2, 45×10-5ч–1;

) = 2, 5× 10-5 × 0, 98 = 2, 45× 10-5ч–1;

) = 2, 5× 10-5 × 0, 97 = 2, 425× 10-5ч–1;

) = 2, 5× 10-5 × 0, 95 = 2, 375× 10-5ч–1;

t_ср = 1;

l

tср =

 

2, 5× 10^-5

= 4 × 10^-4 ч.

Пример 13

Время работы изделия до отказа подчиняется закону распределения Рэлея. Требуется определить количественные характеристики: P(t), f(t), λ (t), t_ср при t₁ = 500 ч, t₂ = 1000 ч, t₃ = 2000 ч, если параметр распределения σ = 1000 ч.

 

Дано:

t₁ = 500 ч t₂ = 1000 ч t₃ = 2000 ч

Решение:

Необходимо      воспользоваться      формулами, соответствующими закону распределения Рэлея (табл. 1. 1)

 σ = 1000 ч

Найти:

f (t ) =

t e-

t 2;

P(t)

s 2  2s

-4

2

f(t)

f (500) =

-

e

2 = 4 × 10

ч–1;

λ (t)

10002 2× 1000

tср

f (1000) =

1000 -

e

2 = 6, 1× 10^-4

ч–1;

10002 2× 1000

f (2000) =

1000²

- 2000                      -4

e      = 2, 7 × 10

2

2× 1000

ч–1;

2s

P(t ) = ò  f (t)dt = e- t 2 ;

P (500)=e-

2× 1000

2 = 0, 88;

( ) e

2

P 1000 = - 1000 2 = 0, 61;

2× 1000

( ) e

2

P 2000 = - 2000 2 = 0, 14;

2× 1000

l (t ) =

f (t);

P(t)

l (500) = 4 ×  10-4 = 4, 5 × 10^-4 ч–1;

0, 88

l         6, 1 × 10   -3

-4

(1000) =         = 10 0, 61

ч–1;

l (2000) = 2, 7 ×  10-4

0, 14

= 1, 93 × 10^-3 ч–1;

tcp

t

= 1;

l

(500) =  1

 

 

= 2, 2 × 10^-3 ч;

^cp        4, 5 × 10^-4

tcp

(1000) =

 

10-3

= 10³ ч;

tcp

(2000) =

 

19, 3 × 10^-4

= 0, 05 × 10⁴ = 500 ч.

 

Пример 14

Время безотказной работы гироскопического устройства с шарикоподшипниками в осях ротора гироскопа подчиняется закону Вейбулла – Гнеденко с параметрами k = 1, 5, λ _о = 10^–4 ч^–1, а время его работы t = 100 ч. Требуется вычислить количественные характеристики надежности такого устройства.

 

Дано:

k = 1, 5

λ о = 10–4 ч–1

 t = 100 ч   Найти:

P(t)

Решение:

Используются формулы закона Вейбулла – Гнеденко для определения количественных характеристик.

Определяется вероятность безотказной работы:

P(t ) = e^-lo × tk ;

f(t)

λ (t)

P (100) = e-104 × 1001, 5

= 0, 9.

tср

Частота отказов определяется по формуле

 

Тогда

f (t ) = l0

ktk -1 ×  e-l0tk .

f (100) =10^-4 × 1, 5× 100^{0, 5} × 0, 9 =1, 35× 10^-3 ч–1 Интенсивность отказов определяется по формуле

l (t ) =

l

f (t);

P(t)

f (100) 1, 35× 10^-3

 

 

-3 ч–1.

(100) =         =            = 1, 5× 10

P(100)    0, 9

Вычисляется средняя наработка до первого отказа

t = Г ( 1 +1) / l^{1/ k} .

cp       k       0

Сначала вычисляют значение гамма-функции, воспользовавшись справочными данными (Приложение 1):

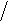
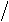x = (1 k ) +1 = (1 1, 5) +1 = 1, 67.

Значения гамма-функции

х	Г (х)
1, 67	0, 90330

Полученные значения подставляют в формулу:

tcp

= 0, 90330 /(10-4)1/1, 5 » 418 ч.

Пример 15

Известно, что интенсивность отказов λ = 0, 02 ч^–1, а среднее время восстановления t_В = 10 ч. Требуется вычислить коэффициент готовности и функцию готовности изделия.

 

Решение:

Коэффициент готовности изделия определяется по формуле

KG =

Тср .

Тср + tВ

Средняя наработка до первого отказа равна tср

Тогда

= 1/ l.

Г

К =  1/ l,

1/ l + tВ

КГ =

1/ 0, 02

 

1/ 0, 02 +10

= 0, 83.

Функция готовности изделия определяется по формуле

РГ (t ) = KG + (1- КГ )е^{-t / K}GtВ,

где t – любой момент времени, при t = 0 система находится в исправном состоянии.

РГ (t ) = 0, 83 + (1- 0, 83)е^{-t / 0, 83× 10} = 0, 83 + 0, 17e^{-0, 12t}.

 

 

Пример 16

Система состоит из 12 600 элементов, средняя интенсивность отказов которых λ _ср = 0, 32·10^–6 ч^–1. Необходимо определить вероятность безотказной работы в течение t = 50 ч.

Дано:

N = 12 600

λ _ср= 0, 32·10^–6 ч^–1

Решение:

Интенсивность отказов системы определяется по формуле

 t = 50 ч              l = l

N = 0, 32 × 10-6 × 12 600 = 4, 032 × 10-3 ч–1.

Найти:

P(t)

c      cp

Вероятность   безотказной   работы   по экспоненциальному закону равна:

P (50) = e-lct = е-4, 032× 10-3× 50 » 0, 82.

 

Пример 17

Система состоит из N = 5 блоков. Надежность блоков характеризуется вероятностью безотказной работы в течение времени t, которая равна: p₁(t) = 0, 98; p₂(t) = 0, 99; p₃(t) = 0, 97; p₄(t) = 0, 985; p₅(t) = 0, 975. Требуется определить вероятность безотказной работы системы.

 

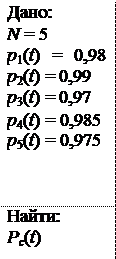Решение:

Необходимо воспользоваться формулой для определения безотказной работы системы:

Pc (t) =

N

Õ

i=1

pi (t) = 0, 98 × 0, 99 × 0, 97 × 0, 985 × 0, 975 = 0, 904.

Вероятности p₁(t), p₂(t), p₃(t), p₄(t), p₅(t) близки к единице, поэтому вычислить Р_с(t) удобно, пользуясь приближенной формулой.

В данном случае q₁ = 0, 02; q₂ = 0, 01; q₃ = 0, 03; q₄ = 0, 015;

q₅ = 0, 025. Тогда

 

 

5                         5

Pc (t) = Õ  pi (t) » 1- å  qi (t) = 1- (0, 02 + 0, 01+ 0, 03 + 0, 015 + 0, 025) = 0, 9.

i=1                     i=1

 

Пример 18

Система состоит из трех устройств. Интенсивность отказов электронного устройства равна λ ₁ = 0, 16·10^–3 ч^–1 = const. Интенсивности отказов двух электромеханических устройств линейно зависят от времени и определяются следующими формулами: λ ₂ = 0, 23·10 ^–4t ч^–1,

λ ₃ = 0, 06·10^–6t^{2, 6} ч^–1. Нужно рассчитать вероятность безотказной работы изделия в течение 100 ч.

Дано:

N = 3

Решение:

Так как λ ≠ const, то на основании формулы

λ ₁ = 0, 16·10^–3 ч^–1

æ N t                 ö

λ ₂ = 0, 23·10^–4t ч^–1

Pc (t ) = expç -å  ò  lt(t)dt ÷

λ ₃ = 0, 06·10^–6t^{2, 6} ч ^–1

 t = 100 ч            Найти:

Р(t)

è i=10                ø

можно написать

t

c                     í ê ò  1                ò 2

P (t ) = expì - é t l (t )dt + l

 

t

3    ú ý

(t )dt + ò  l (t )dt ù ü  =

î ë 0                      0                       0                 û þ

=   é æ

-4 t 2

-6 t3, 6 ö ù

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: