 |
Вероятность безотказной работы от времени - Р
|
|
|
|
Вероятность безотказной работы от времени - Р
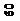
Кол - во часов работы
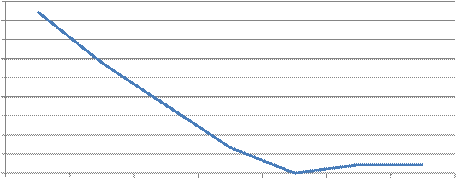
Частота отказов от времени, f
0. 045
0. 040
0. 035
0. 030
0. 025
0. 020
0. 015
0. 010
0. 005
0. 000
Кол-во часов работы
Интенсивность отказов от времени, λ
0. 2500
0. 2000
0. 1500
0. 1000
0. 0500
0. 0000
Кол-во часов работы
Вывод. Вероятность безотказной работы радиоэлектронного оборудования падала на всем процессе наблюдений и изменялась от 0, 58 до 0.
Частота отказов после 5 часов работы радиоэлектронного оборудования составила 4, 2·10-2 ч. Далее частота отказов падала и после 45 часов работы частота достигла нуля. Далее до конца наблюдения частота отказов держалась на отметке 2·10-3 ч.
Интенсивность отказов в промежутке времени до 25 часов работы радиоэлектронного оборудования увеличивалась от 53, 5 · 10-3 ч до 88, 9·10-3 ч. Далее интенсивность отказов падала и на отметке 45 часов достигла нуля. Потом интенсивность резко увеличилась и в конце наблюдения составила 0, 2 ч.
Пример 29
На испытание поставлено N=1000 элементов. Число отказов фиксировалось в каждом интервале времени испытаний Δ t=500ч. Требуется определить вероятность безотказной работы, частоту отказов и интенсивность отказов в функции времени, построить графики этих функций, а также найти среднюю наработку до первого отказа элементов. Данные об отказах элементов:
| Δ ti, ч | n(Δ ti) | Δ ti, ч | n(Δ ti) |
| 0-500 | 4500-5000 | ||
| 500-1000 | 5000-5500 | ||
| 1000-1500 | 5500-6000 | ||
| 1500-2000 | 6000-6500 | ||
| 2000-2500 | 6500-7000 | ||
| 2500-3000 | 7000-7500 | ||
| 3000-3500 | 7500-8000 | ||
| 3500-4000 | 8000-8500 | ||
| 4000-4500 |
Решение.
Вычислим Р(t) по формуле:
|
|
|
P(t) = (N 0 - n(t))
N 0
P(500) = 1000 -145 = 0. 855;
P(1000) = 1000 - 231 = 0. 769;
1000
P(1500) = 1000 - 308 = 0. 692;
P(2000) = 1000 - 377 = 0. 623;
P(2500) = 1000 - 439 = 0. 561;
1000
P(3000) = 1000 - 495 = 0. 505;
P(3500) = 1000 - 546 = 0. 454;
P(4000) = 1000 - 591 = 0. 409;
1000
P(4500) = 1000 - 632 = 0. 368;
P(5000) = 1000 - 669 = 0. 331;
P(5500) = 1000 - 702 = 0. 298;
1000
P(6000) = 1000 - 737 = 0. 263;
P(6500) = 1000 - 797 = 0. 203;
P(7000) = 1000 - 872 = 0. 128;
1000
P(7500) = 1000 - 934 = 0. 066;
P(8000) = 1000 - 976 = 0. 024;
P(8500) = 1000 - 992 = 0. 008;
1000
Найдем частоту отказов по формуле:
f(t)= n(Δ t)
N0·Δ t
f(250)= 145
1000 ∙ 500
f(1250)= 77
= 0, 29·10-3; f(750)= 86 1000 ∙ 500
= 0, 15·10-3; f(1750)= 69
= 0, 17·10-3;
= 0, 14·10-3;
1000 ∙ 500
f(2250)= 62
1000 ∙ 500
f(3250)= 51
1000 ∙ 500
f(4250)= 41
1000 ∙ 500
f(5250)= 33
1000 ∙ 500
f(6250)= 60
1000 ∙ 500
f(7250)= 62
1000 ∙ 500
1000 ∙ 500
= 0, 12·10-3; f(2750)= 56
1000 ∙ 500
= 0, 10·10-3; f(3750)= 45
1000 ∙ 500
= 0, 08·10-3; f(4750)= 37
1000 ∙ 500
= 0, 06·10-3; f(5750)= 35
1000 ∙ 500
= 0, 12·10-3; f(6750)= 75
1000 ∙ 500
= 0, 12·10-3; f(7750)= 42
1000 ∙ 500
= 0, 11·10-3;
= 0, 09·10-3;
= 0, 07·10-3;
= 0, 07·10-3;
= 0, 15·10-3;
= 0, 08·10-3;
f(8250)= 16
1000 ∙ 500
= 0, 03·10-3
Найдем интенсивность отказов по формуле: λ (t) = n(Δ t)
Δ t∙ 𝑁 ср
l(250) =
500 × æ 1000 + 855 ö
= 3, 1× 10-4;
l(750) =
500 × æ 855 + 769 ö
= 2, 1× 10-4;
ç 2 ÷ ç 2 ÷
l(1250) =
è ø
500 × æ 769 + 692 ö
= 2, 1× 10-4;
l(1750) =
è ø
500 × æ 692 + 623 ö
= 2, 1× 10-4;
ç 2 ÷ ç 2 ÷
l(2250) =
è ø
500 × æ 623 + 561 ö
= 2, 1× 10-4;
l(2750) =
è ø
500 × æ 561+ 505 ö
= 2, 1× 10-4;
ç 2 ÷ ç 2 ÷
l(3250) =
è ø
500 × æ 505 + 454 ö
= 2, 1× 10-4;
l(3750) =
è ø
|
|
|
500 × æ 454 + 409 ö
= 2, 1× 10-4;
ç 2 ÷ ç 2 ÷
l(4250) =
è ø
500 × æ 409 + 368 ö
= 2, 1× 10-4;
l(4750) =
è ø
500 × æ 368 + 331 ö
= 2, 1× 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(5250) =
500 × æ 331+ 298 ö
= 2, 1× 10-4;
l(5750) =
500 × æ 298 + 263 ö
= 2, 5 × 10-4;
ç 2 ÷ ç 2 ÷
l(6250) =
è ø
500 × æ 263 + 203 ö
= 5, 2 × 10-4;
l(6750) =
è ø
500 × æ 203 +128 ö
= 9, 1× 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(7250) =
500 × æ 128 + 66 ö
= 12, 8 × 10-4;
l(7750) =
500 × æ 66 + 24 ö
= 18, 7 × 10-4;
ç 2 ÷ ç 2 ÷
è ø
l(8250) =
500 × æ 24 + 8 ö
è ø
= 20 × 10-4;
ç 2 ÷
è ø
Значения Р(t), f(t), λ (t), вычисленные для всех Δ ti.
| Δ ti, ч | P(t) | f(t), ч | λ (t), ч |
| 0 – 500 | 0, 855 | 0, 00029 | 0, 00031 |
| 500 – 1000 | 0, 769 | 0, 00017 | 0, 00021 |
| 1000 – 1500 | 0, 692 | 0, 00015 | 0, 00021 |
| 1500 – 2000 | 0, 623 | 0, 00014 | 0, 00021 |
| 2000 – 2500 | 0, 561 | 0, 00012 | 0, 00021 |
| 2500 – 3000 | 0, 505 | 0, 00011 | 0, 00021 |
| 3000 – 3500 | 0, 454 | 0, 00010 | 0, 00021 |
| 3500 – 4000 | 0, 409 | 0, 00009 | 0, 00021 |
| 4000 – 4500 | 0, 368 | 0, 00008 | 0, 00021 |
| 4500 – 5000 | 0, 331 | 0, 00007 | 0, 00021 |
| 5000 – 5500 | 0, 298 | 0, 00007 | 0, 00021 |
| 5500 – 6000 | 0, 263 | 0, 00007 | 0, 00025 |
| 6000 – 6500 | 0, 203 | 0, 00012 | 0, 00052 |
| 6500 – 7000 | 0, 128 | 0, 00015 | 0, 00091 |
| 7000 – 7500 | 0, 066 | 0, 00012 | 0, 00128 |
| 7500 – 8000 | 0, 024 | 0, 00008 | 0, 00187 |
| 8000 – 8500 | 0, 008 | 0, 00003 | 0, 00200 |
Находим среднюю наработку до первого отказа.
Учитывая, что в данном случае:
m=tk/Δ t=8500/500=17; N0=992;
имеем:
å nitcpi Tcp = i=1 =
N0
145* 250 + 86* 750 + 77 *1250 +... + 62* 7250 + 42* 7750 +16*8250
= 3486. 391
|
|
|
Строим графики функций
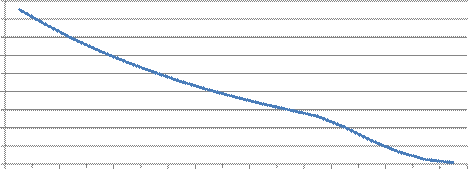
Вероятность безотказной работы от
0. 9
0. 8
0. 7
0. 6
0. 5
0. 4
0. 3
0. 2
0. 1
0
времени - Р
Кол - во часов работы
Частота отказов от времени, f
0. 00035
0. 00030
0. 00025
0. 00020
0. 00015
0. 00010
0. 00005
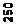
0. 00000
Кол-во часов работы
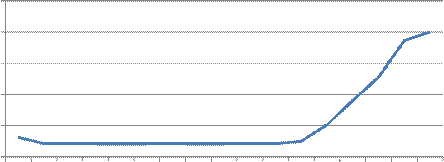
Интенсивность отказов от времени, λ
0. 00250
0. 00200
0. 00150
0. 00100
0. 00050
0. 00000
Кол-во часов работы
Вывод. Вероятность безотказной работы после 500 часов испытаний составила 0, 855 и падала на всем процессе испытаний до нуля.
Частота отказов после 250 часов работы составила 2, 9·10-4 ч и падала до 5750 часов испытаний и достигла 0, 7·10-4 ч. Далее до 6750 часов работы частота отказов увеличивалась до 1, 5 · 10-4 ч. Далее до конца наблюдений частота падала и в конце наблюдений она составила 0, 3·10-4 ч. В процессе наблюдений от 250 до 5750 часов интенсивность отказов держалась на уровне 2, 1 · 10-4 ч. Далее до конца наблюдений интенсивность увеличивалась и в конце составила 20·10-4 ч.
Пример 30
Имеются статистические данные об отказах трех групп одинаковых изделий. В каждой группе было по 100 изделий, и их испытания проводились по 1 группе 550 ч, по 2 группе 400 ч и по 3 группе 200 ч. Необходимо вычислить количественные характеристики P(t), f(t), λ (t) и построить графики этих функций.
| Δ ti, ч | Количество отказов n(Δ ti) по группам изделий | Σ n(Δ ti) | ||
| 1 группа | 2 группа | 3 группа | ||
| 0-25 | ||||
| 25-50 | ||||
| 50-75 | ||||
| 75-100 | ||||
| 100-150 | ||||
| 150-200 | ||||
| 200-250 | - | |||
| 250-300 | - | |||
| 300-400 | - | |||
| 400-550 | - | - | ||
Решение.
Вычислим количественные характеристики для 1 группы. Вычислим Р(t) по формуле:
P(t) = (N 0 - n(t))
N 0
P(25) = 100 - 4 = 0. 96;
P(100) = 100 - 21 = 0. 79;
P(50) = 100 -12 = 0. 88;
100
P(150) = 100 - 26 = 0. 74;
P(75) = 100 -18 = 0. 82;
100
P(200) = 100 - 30 = 0. 7;
P(250) = 100 - 31 = 0. 69;
P(300) = 100 - 33 = 0. 67;
100
P(550) = 100 - 41 = 0. 59;
P(400) = 100 - 36 = 0. 64;
100
Рассчитываем частоту отказов по формуле:
f (t) = n(Dt)
N0Dt
f (12, 5) =
100 × 25
= 16 × 10-4;
|
|
|
f (37, 5) =
100 × 25
= 32 × 10-4;
f (62, 5) =
100 × 25
= 24 × 10-4;
f (87, 5) =
100 × 25
= 12 × 10-4;
f (125) =
100 × 50
= 10 × 10-4;
f (175) =
100 × 50
= 8× 10-4;
f (225) =
100 × 50
= 2 × 10-4;
f (275) =
100 × 50
= 4 × 10-4;
f (350) =
100 × 100
= 3× 10-4;
f (475) =
100 × 150
= 3, 3× 10-4;
Рассчитываем интенсивность отказов по формуле:
l(12, 5) =
25 × æ 100 + 96 ö
l(t) =
= 16, 3× 10-4;
n(Dt)
Ncp Dt
l(37, 5) =
25 × æ 96 + 88 ö
= 34, 8 × 10-4;
ç 2 ÷ ç 2 ÷
l(62, 5) =
è ø
25 × æ 88 + 82 ö
= 28, 2 × 10-4;
l(87, 5) =
è ø
25 × æ 82 + 79 ö
= 14, 9× 10-4;
ç 2 ÷ ç 2 ÷
l(125) =
è ø
50 × æ 79 + 74 ö
= 13, 1× 10-4;
l(175) =
è ø
50 × æ 74 + 70 ö
= 11, 1× 10-4;
ç 2 ÷ ç 2 ÷
l(225) =
è ø
50 × æ 70 + 69 ö
= 2, 9 × 10-4;
l(275) =
è ø
50 × æ 69 + 67 ö
= 5, 9 × 10-4;
ç 2 ÷ ç 2 ÷
l(350) =
è ø
100 × æ 67 + 64 ö
= 4, 6 × 10-4;
l(475) =
è ø
150 × æ 64 + 59 ö
= 5, 4 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
Вычислим количественные характеристики для 2 группы. Вычислим Р(t) по формуле:
P(t) = (N 0 - n(t))
N 0
P(25) = 100 - 6 = 0. 94;
P(100) = 100 - 24 = 0. 76;
P(250) = 100 - 35 = 0. 65;
P(50) = 100 -15 = 0. 85;
100
P(150) = 100 - 29 = 0. 71;
P(300) = 100 - 37 = 0. 63;
P(75) = 100 - 20 = 0. 8;
100
P(200) = 100 - 32 = 0. 68;
P(400) = 100 - 41 = 0. 59;
Рассчитываем частоту отказов по формуле:
f (t) = n(Dt)
N0Dt
f (12, 5) =
100 × 25
= 24 × 10-4;
f (37, 5) =
100 × 25
= 36 × 10-4;
f (62, 5) =
100 × 25
= 20 × 10-4;
f (87, 5) =
100 × 25
= 16 × 10-4;
f (125) =
100 × 50
= 10 × 10-4;
f (175) =
100 × 50
= 6 × 10-4;
f (225) =
100 × 50
= 6 × 10-4;
f (275) =
100 × 50
= 4 × 10-4;
f (350) =
100 × 100
= 4 × 10-4;
Рассчитываем интенсивность отказов по формуле:
l(12, 5) =
25 × æ 100 + 94 ö
l(t) =
= 24, 7 × 10-4;
n(Dt)
Ncp Dt
l(37, 5) =
25 × æ 94 + 85 ö
|
|
|
= 40, 2 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(62, 5) =
25 × æ 85 + 80 ö
= 24, 2 × 10-4;
l(87, 5) =
25 × æ 80 + 76 ö
= 20, 5 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(125) =
50 × æ 76 + 71 ö
= 13, 6 × 10-4;
l(175) =
50 × æ 71+ 68 ö
= 8, 6 × 10-4;
ç 2 ÷ ç 2 ÷
l(225) =
è ø
50 × æ 68 + 65 ö
= 9 × 10-4;
l(275) =
è ø
50 × æ 65 + 63 ö
= 6, 3× 10-4;
ç 2 ÷ ç 2 ÷
è ø
l(350) =
100 × æ 63 + 59 ö
è ø
= 6, 6 × 10-4;
ç 2 ÷
è ø
Вычислим количественные характеристики для 3 группы. Вычислим Р(t) по формуле:
P(t) = (N 0 - n(t))
N 0
P(25) = 100 - 5 = 0. 95;
P(100) = 100 - 25 = 0. 75;
P(50) = 100 -13 = 0. 87;
100
P(150) = 100 - 31 = 0. 69;
P(75) = 100 - 20 = 0. 8;
100
P(200) = 100 - 34 = 0. 66;
Рассчитываем частоту отказов по формуле:
f (t) = n(Dt)
N0Dt
f (12, 5) =
100 × 25
= 20 × 10-4;
f (37, 5) =
100 × 25
= 32 × 10-4;
f (62, 5) =
100 × 25
= 28× 10-4;
f (87, 5) =
100 × 25
= 20 × 10-4;
f (125) =
100 × 50
= 12 × 10-4;
f (175) =
100 × 50
= 6 × 10-4;
Рассчитываем интенсивность отказов по формуле:
l(12, 5) =
25 × æ 100 + 95 ö
l(t) =
= 20, 5 × 10-4;
n(Dt)
Ncp Dt
l(37, 5) =
25 × æ 95 + 87 ö
= 35, 2 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(62, 5) =
25 × æ 87 + 80 ö
= 33, 5 × 10-4;
l(87, 5) =
25 × æ 80 + 75 ö
= 25, 8 × 10-4;
ç 2 ÷ ç 2 ÷
l(125) =
è ø
50 × æ 75 + 69 ö
= 16, 7 × 10-4;
l(175) =
è ø
50 × æ 69 + 66 ö
= 8, 9 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
Вычислим количественные характеристики для суммы трех групп.
Вычислим Р(t) по формуле:
P(t) = (N 0 - n(t))
N 0
P(25) = 300 -15 = 0. 95;
P(100) = 300 - 70 = 0. 77;
P(250) = 300 -100 = 0. 67;
P(50) = 300 - 40 = 0. 87;
300
P(150) = 300 - 86 = 0. 71;
P(300) = 300 -104 = 0. 65;
P(75) = 300 - 58 = 0. 81;
300
P(200) = 300 - 96 = 0. 68;
P(400) = 300 -111 = 0. 63;
P(550) = 300 -116 = 0. 61;
Рассчитываем частоту отказов по формуле:
f (t) = n(Dt)
N0Dt
f (12, 5) =
300 × 25
= 20 × 10-4;
f (37, 5) =
300 × 25
= 33, 3× 10-4;
f (87, 5) = 12
f (62, 5) =
= 16 × 10-4;
300 × 25
= 24 × 10-4;
f (125) = 16
= 10, 7 × 10-4;
300 × 25 300 × 50
f (175) =
f (275) =
300 × 50
300 × 50
= 6, 7 × 10-4;
= 2, 7 × 10-4;
f (225) =
f (350) =
300 × 50
300 × 100
= 2, 7 × 10-4;
= 2, 3× 10-4;
f (475) =
300 × 150
= 1, 1× 10-4;
Рассчитываем интенсивность отказов по формуле:
l(12, 5) =
25 × æ 300 + 285 ö
l(t) =
= 20, 5 × 10-4;
n(Dt)
Ncp Dt
l(37, 5) =
25 × æ 285 + 260 ö
= 36, 7 × 10-4;
ç 2 ÷ ç 2 ÷
l(62, 5) =
è ø
25 × æ 260 + 242 ö
= 28, 7 × 10-4;
l(87, 5) =
è ø
25 × æ 242 + 230 ö
= 20, 3× 10-4;
ç 2 ÷ ç 2 ÷
l(125) =
è ø
50 × æ 230 + 214 ö
= 14, 4 × 10-4;
l(175) =
è ø
50 × æ 214 + 204 ö
= 9, 6 × 10-4;
ç 2 ÷ ç 2 ÷
l(225) =
è ø
50 × æ 204 + 200 ö
= 4 × 10-4;
l(275) =
è ø
50 × æ 200 +196 ö
= 4 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
l(350) =
100 × æ 196 +189 ö
= 3, 6 × 10-4;
l(475) =
150 × æ 189 +185 ö
= 1, 8 × 10-4;
ç 2 ÷ ç 2 ÷
è ø è ø
Значения P(t), всех Δ ti всех трех групп сведем в таблицу:
| Δ ti, ч | P(t) 1 группы | P(t) 2 группы | P(t) 3 группы | P(t) трех групп |
| 0-25 | 0, 96 | 0, 94 | 0, 95 | 0, 95 |
| 25-50 | 0, 88 | 0, 85 | 0, 87 | 0, 87 |
| 50-75 | 0, 82 | 0, 8 | 0, 8 | 0, 81 |
| 75-100 | 0, 79 | 0, 76 | 0, 75 | 0, 77 |
| 100-150 | 0, 74 | 0, 71 | 0, 69 | 0, 71 |
| 150-200 | 0, 7 | 0, 68 | 0, 66 | 0, 68 |
| 200-250 | 0, 69 | 0, 65 | - | 0, 67 |
| 250-300 | 0, 67 | 0, 63 | - | 0, 65 |
| 300-400 | 0, 64 | 0, 59 | - | 0, 63 |
| 400-550 | 0, 59 | - | - | 0, 61 |
Значения f(t), вычисленные для всех Δ ti всех тр
|
|
|
