1.4 Примеры решения задач. = 0,0067 = 6,7 ×10-3 ч–1;. Последнее выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t

T

m В =,

t _В

К Г =

T

T + tВ

(1. 35)

Последнее выражение устанавливает зависимость между коэффициентом готовности системы и вероятностью застать ее в исправном состоянии в любой момент времени t.

Из (1. 34) видно, что P_Г(t) → К_Г при t → ∞, т. е. практически коэффициент готовности имеет смысл вероятности застать объект в исправном состоянии при установившемся процессе эксплуатации.

В некоторых случаях критериями надежности восстанавливаемых систем могут быть также показатели безотказности невосстанавливаемых систем, например: вероятность безотказной работы, частота отказов, средняя наработка до отказа, интенсивность отказов. Такая необходимость возникает всегда, когда имеет смысл оценить надежность восстанавливаемой системы до первого отказа, а также в случае, когда применяется резервирование с восстановлением резервных устройств, отказавших в процессе работы системы, причем отказ всей резервированной системы не допускается.

1. 4 Примеры решения задач

Пример 1

Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За 3000 ч отказало 80 ламп, требуется определить вероятность безотказной работы P(t) и вероятность отказа Q(t) в течение 3000 ч

 

Дано:                     Решение:

N = 1000 шт.

∆ t = 3000 ч

 n = 80 шт.       

P(t) =

N - n(t);

N

1000 - 80

Найти: Р(t)

Q(t)

P(t) =             = 0, 92;

1000

Q(3000) =1- P(3000) = 0, 08

 

или

 

Пример 2

Q(3000) = n(t) =

N

 

= 0, 08.

Допустим, что на испытание поставлено 1000 однотипных электронных ламп. За первые 3000 ч отказало 80 ламп, а за интервал времени 3000–4000 ч отказало еще 50 ламп. Требуется определить частоту f(∆ t) и интенсивность λ (∆ t) отказов электронных ламп в промежутке времени ∆ t = 3000–4000 ч.

 

Дано:                       Решение:

N = 1000 шт.

∆ t₁ = 3000 ч

n₁ = 80 шт.

∆ t₂ = [3000, 4000]

 n₂ = 50 шт.        

f (Dt 2) =

 

f (Dt2) =

n(Dt 2);

N × Dt 2

50   = 5

1000 × 1000

 

 

× 10-5

 

 

ч–1;

Найти:

l(Dt ) =

n(Dt 2),

f(∆ t)

λ (∆ t)

NСР

× Dt 2

 

 

где

NСР =

N РАБ 1 + NРАБ 2

2       ;

NРАБ 1 =1000 - 80 = 920 шт.;

NРАБ 2 =1000 -130 = 870 шт.;

NCP

= (1000 - 80) + (920 - 50) = 895

2

 

 

шт.;

l(Dt

₂) =

 

895× 1000

= 5, 58 × 10^-5

 

ч–1.

 

Пример 3

t=3000 ÷        Dt=100 ÷

На испытание поставлено N₀ = 400 изделий. За время t = 3000 ч отказало n(t) = 200 изделий, за интервал ∆ t = 100 ч отказало n(∆ t) = 100 изделий. Требуется определить вероятность безотказной работы за 3000 ч, вероятность безотказной работы за 3100 ч, вероятность безотказной работы за 3050 ч, частоту отказов f(3050), интенсивность отказов λ (3050).

N=400                       n(t)=200 n(Dt)=100

Рис. 1. 3. Временной график

 

Дано:

N = 400 шт.

t = 3000 ч

n = 200 шт.

∆ t = 100 ч

 n(∆ t) = 100 шт.

Решение:

Вероятность безотказной работы определяется по формуле

P(t) = N - n(Dt ) .

N

Для t = 3000 ч (начало интервала)

Найти:

Р(3000) Р(3100)

P(3000) =

N 0 - n(3000) N ₀

= 400 - 200 = 0, 5.

400

Р(3050)

Для t = 3100 ч (конец интервала)

f(3050)

N 0 - n(3100)

400 - 300      .

f(3000) f(3100) λ (3000) λ (3050)

P(3100) =                    =             = 0, 25

N 0                          400

Среднее время исправно работающих изделий в интервале ∆ t:

λ (3100)

N ср =

Nt + Nt+1 = 200 +100 = 150.

2               2

Число изделий, отказавших за время t = 3050 ч:

n (3050) = N 0 - N ср = 400 -150 = 250, тогда

P (3050) = 400 - 250 = 0, 375.

Определяется частота отказа:

f (3050) =

n(Dt ) N × Dt

f (3050) =

 

400× 100

= 0, 0025 = 2, 5 × 10-4

ч–1.

Так же определяется частота отказов за интервалы 3000 и 3100 ч, причем началом интервалов является t = 0.

f (3000) =

 

400 × 3000

= 0, 000167 = 1, 67 × 10-4 ч–1;

f (3100) =

 

400 × 3100

= 0, 00024 = 2, 4 × 10^-4

ч–1.

Определяется интенсивность отказов:

а) в интервале ∆ t = 3050 ч,

l (3050) =  n(Dt ) ;

N СР × Dt

l (3050) =

 

150 × 100

= 0, 0067 = 6, 7 × 10-3 ч–1;

б) в интервале Dt = 3000 ч,

N cp (3000) = 400 -100 = 300 шт.;

l (3000) =

 

300 × 3000

= 0, 000222 = 2, 22 × 10-4 ч–1;

в) в интервале Dt = 3100 ч,

N cp (3100) = 400 -150 = 250

шт.;

l (3100) =

 

Пример 4

 

250 × 3000

= 0, 00039 = 3, 9 × 10^-4

ч–1.

На испытание поставлено 10 изделий. За время t=1000 ч вышло из строя n(t)=3 штук изделий. За последующий интервал времени Δ t=100 ч вышло из строя n(Δ t)=1 штук изделий. Необходимо вычислить вероятность безотказной работы за время t и t + Δ t, частоту отказов и интенсивность отказов на интервале Δ t.

 

Дано:

N₀ = 10 шт.

Решение:

Определяем вероятность безотказной работы.

t = 1000 ч

∆ t = 100 ч

Р(t)= 𝑁 0 − 𝑛 (𝑡 )

𝑁 0

; Р(1000)= ^{10− 3} = 0, 7

10

 n(t) = 3 шт.

Вероятность безотказной работы за время t + Δ t.

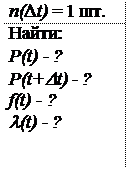Р(1100)= ^{𝑁 0− 𝑛 (𝑡 )}

𝑁 0

Р(1100)= ^{10− 4} = 0, 6

10

Найдем частоту отказов.

f(100)= ^{n(Δ t)}

𝑁 0 Δ t

f(100)= ¹

10∙ 100

= 1·10^-3 ч^-1

Найдем интенсивность отказов.

λ (100) =  ^{n(Δ t)}

Δ t·Nср

λ (100) =     ¹     = 1·10^-5ч^-1

100· 997 +996

Ответ: P(t)=0, 7; P(t+Δ t) =0, 6; f(t)= 1·10^-3 ч^-1; λ (t)= 1·10^-5ч^-1.

Пример 5

В течение некоторого периода времени производилось наблюдение за работой одного объекта. За весь период зарегистрировано n = 15 отказов. До начала наблюдений объект проработал 258 ч, к концу наблюдения наработка составила 1233 ч. Определить среднюю наработку на отказ t_ср.

 

Дано:

n = 15

t₁ = 258 ч

 t₂ = 1233 ч      Найти:

Решение:

Наработка за указанный период составила

∆ t = t₁ – t₂ = 1233 – 258 = 975 ч.

Наработка на отказ по статистическим данным определяется по формуле

tср

tср

n

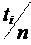= å  ,

i=1

где t_i – время исправной работы между (i – 1) и i отказами;

n – число отказов за некоторое время t.

n

Приняв

å  ti = 975 ч, можно определить среднюю наработку на

i=1

отказ     t_ср = 975 15

= 65 ч.

 

Пример 6

В течение времени Δ t производилось наблюдение за восстанавливаемым изделием и было зафиксировано n(Δ t)=2 отказов. До начала наблюдения изделие проработало в течение времени t₁=1200 ч, общее время наработки к концу наблюдения составило t₂=5558 ч. Требуется найти наработку на отказ.

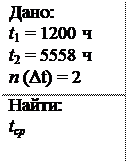Решение:

Найдем наработку изделия за наблюдаемый период. t = t₂ – t₁ = 5558 – 1200 = 4358ч.

𝑖 =1

Принимая - ^𝑛 𝑡 𝑖 = 4358ч.

находим среднюю наработку на отказ:

𝑖 =1

t = 𝑛

𝑡 𝑖

= ⁴³⁵⁸ = 2179 ч.

ср       𝑛              2

где 𝑡 𝑖 - время исправной работы изделия между(i-1) и i-м отказами;

n – число отказов за некоторое время t.

Ответ: Наработка на отказ равна 2179 ч.

 

Пример 7

Производилось наблюдение за работой трех однотипных объектов. За период наблюдения было зафиксировано по первому объекту 6 отказов, по второму – 11 отказов, третьему – 8 отказов. Наработка первого объекта t₁ = 181 ч, второго t₂ = 329 ч, третьего t₃ = 245 ч. Определить наработку объектов на отказ.

 

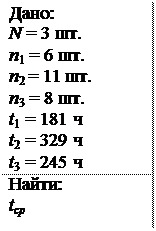Решение:

1-й вариант решения:

tср

n

= å  t_i i=1

ni ;

t = T1 + T 2 + T 3;

^ср n + n + n

tср

1    2     3

= 181+ 329 + 245 = 30, 2 ч;

6 +11+ 8

 

 

2-й вариант решения:

 

tср 1

=  t₁,

n₁

tср 2 =  t 2,

n₂

tср 3 =  t3 ;

n₃

t = 181 = 30, 2 ч;

t = 329 = 29, 9 ч; t

245 = 30, 6 ч;

ср 1    6

ср 2   11

ср 3 8

tср = (30, 2 + 29, 9 + 30, 6)

3 = 30, 2 ч.

Как видно, у задачи есть два варианта решения. Первый основан на использовании общей формулы вычисления средней наработки; второй – более детальный: сначала находится средняя наработка для каждого элемента, а среднее значение этих чисел и есть то, что определяется.

 

Пример 8

Система состоит из 5 приборов, причем отказ любого одного из них ведет к отказу системы. Известно, что первый отказал 34 раза в течение 952 ч работы, второй – 24 раза в течение 960 ч работы, а остальные приборы в течение 210 ч работы отказали 4, 6 и 5 раз соответственно. Требуется определить наработку на отказ системы в целом, если справедлив экспоненциальный закон надежности для каждого из пяти приборов.

 

Дано:

N = 5 шт.

Решение:

N

Используются следующие соотношения:

n₁ = 34 шт.

n₂ = 24 шт.

l_c = å  l_i ;

tcp =.

n = 4 шт.

i=1                           l с

n₄ = 6 шт.

Определяется интенсивность отказов для каждого

прибора (N = 1):

n₅ = 5 шт. t₁ = 952 ч t₂ = 960 ч

li =

N

n  ,

_ср × Dt

 t_3–5 = 210 ч      Найти:

где N_ср – среднее число исправно работающих

изделий в интервале ∆ t.

tср

l1 =

l3 =

 

 

= 0, 0357 ч^–1;

= 0, 02 ч–1;

l2 =

 

= 0, 025 ч^–1;

 

 

или

l4 =

 

= 0, 03 ч ^–1;

l5 =

 

= 0, 02

ч–1;

n

å  l

i=1

 

3... 5

= 4 + 6 + 5 = 0, 0714 ч^–1;

210

тогда интенсивность отказов системы будет

N

lc =

å  li = l1 + l2 + l3... 5 = 0, 0357 + 0, 025 + 0, 0714 = 0, 135

i=1

ч–1.

Средняя наработка на отказ системы равна

1      1

tcp = lc

= 0, 135

= 7, 57 ч.

Пример 9

Система состоит из 5 приборов, имеющих разную надежность. Известно, что каждый из приборов, поработав вне системы в течении времени t₁=600 ч, имел n_i=45 отказов. Для каждого из приборов справедлив экспоненциальный закон надежности. Необходимо найти наработку на отказ всей системы.

 

Дано:         Решение:

N = 5 шт.

𝑛

     𝑡

𝑡        600

t = 600 ч

tcp=   𝑖 =1 𝑐 𝑝 𝑖 ; 𝑡

=  1  =

= 13. 3ч; 𝑡   =

= 300ч;

1

n₁ = 45

t₂ = 600 ч

𝑛            𝑐 𝑝 1

 

𝑡   = 200 = 50ч; 𝑡

𝑛 1           45

 

= 200 = 33. 3ч; 𝑡

𝑐 𝑝 2       2

 

= 200 = 100ч;

n₂ = 2

𝑐 𝑝 3        4

𝑐 𝑝 4        6

𝑐 𝑝 5        2

t₃ = 200 ч

n₃ = 4

t₄ = 200 ч

n₄ = 6

t₅ = 200 ч

 n₅ = 2       Найти:

tср

Ответ: По имеющимся данным можем определить время только до первого отказа всей системы.

 

Пример 10

За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 8 отказов. Время восстановления составило: t₁ = 12 мин, t₂ = 23 мин, t₃ = 15 мин, t₄ = 9 мин, t₅ = 17 мин, t₆ = 28 мин, t₇ = 25 мин, t₈ =

31 мин. Требуется определить среднее время восстановления аппаратуры.

 

Дано:

n = 8 отказов

t₁ = 12 мин

Решение:

n

å  t_i

t₂ = 23 мин

tcp. в = i=1  ;

n

t₃ = 15 мин t₄ = 9 мин t₅ = 17 мин t₆ = 28 мин t₇ = 25 мин

 t₈ = 31 мин

tср. в =

12 + 23 +15 + 9 +17 + 28 + 25 + 31

 

= 20 мин.

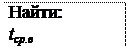
Пример 11

Аппаратура имела среднюю наработку на отказ t_cp = 65 ч и среднее время восстановления t_в = 1, 25 ч. Требуется определить коэффициент готовности К_г.

 

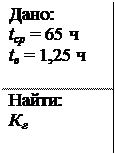Решение:

г

К =  t_cp ;

tcp + tв

=

65

К

 

= 0, 98.

 

^г 65 +1, 25

 

 

Пример 12

Пусть время работы элемента до отказа подчинено экспоненциальному закону λ = 2, 5·10^–5 ч^–1. Требуется определить вероятность безотказной работы P(t), частоту отказов f(t) и среднюю наработку на отказ t_ср, если t = 500, 1000, 2000 ч.

 

Дано:

λ = 2, 5·10^–5

ч–1

Решение:

P(t ) = e^-lt ;

t₁ = 500 ч

t₂ = 1000 ч

P(t1 ) = e-2, 5× 0, 00001× 500 = 0, 98;

P(t2 ) = e-2, 5× 0, 00001× 1000 = 0, 97;

 t₃ = 2000 ч Найти:

P(t3

) = e-2, 5× 0, 00001× 2000 = 0, 95;

P(t)

f(t) tср

 

f (t1 f (t2 f (t3

f (t ) = l × P (t );

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: