 |
Вероятность безотказной работы от времени - Р
|
|
|
|
= 246;
lc =
å
i=1
Nili
= 22, 4 × 10-5
ч–1.
По данным табл. 1. 2 и по формуле для экспоненциального закона находится вероятность безотказной работы изделия в течение t = 200 ч и средняя наработка до первого отказа:
|
-22, 4× 10-5× 200
= e
» 0, 956,

 1 1
1 1
tcp. c
= lc = 22, 4× 10-5
= 4464 ч.
Пример 26
На испытании находилось 1000 однотипных ламп 6Ж4. Число отказавших ламп учитывалось через каждые 1000 часов работы. Требуется определить вероятность безотказной работы, частоту отказов и интенсивность отказов в функции времени, построить графики этих функций. Необходимо также найти среднюю наработку до первого отказа.
| Δ ti, ч | n(Δ ti) | Δ ti, ч | n(Δ ti) |
| 0-1000 | 13000-14000 | ||
| 1000-2000 | 14000-15000 | ||
| 2000-3000 | 15000-16000 | ||
| 3000-4000 | 16000-17000 | ||
| 4000-5000 | 17000-18000 | ||
| 5000-6000 | 18000-19000 | ||
| 6000-7000 | 19000-20000 | ||
| 7000-8000 | 20000-21000 | ||
| 8000-9000 | 21000-22000 | ||
| 9000-10000 | 22000-23000 | ||
| 10000-11000 | 23000-24000 | ||
| 11000-12000 | 24000-25000 | ||
| 12000-13000 | 25000-26000 |
 Дано:
Дано:
N0=1000
Dt=1000 ч Найти:
Р(t)
f(t)
Решение
Определим вероятность безотказной работы.
Р(t)= 𝑁 0 − 𝑛 (𝑡 )
𝑁 0

 Р(1000)= 1000− 20 = 0, 98; Р(2000)= 1000− 45 = 0, 955;
Р(1000)= 1000− 20 = 0, 98; Р(2000)= 1000− 45 = 0, 955;
1000 1000

 l(t)
l(t)
Р(3000)= 1000− 80 = 0, 92; Р(4000)= 1000− 130 = 0, 87;
Tср

 Р(5000)= 1000− 160 = 0, 84; Р(6000)= 1000− 210 = 0, 79;
Р(5000)= 1000− 160 = 0, 84; Р(6000)= 1000− 210 = 0, 79;
1000 1000

 Р(7000)= 1000− 250 = 0, 75; Р(8000)= 1000− 290 = 0, 71;
Р(7000)= 1000− 250 = 0, 75; Р(8000)= 1000− 290 = 0, 71;
1000 1000

 Р(9000)= 1000− 340 = 0, 66; Р(10000)= 1000− 370 = 0, 63;
Р(9000)= 1000− 340 = 0, 66; Р(10000)= 1000− 370 = 0, 63;
1000 1000

 Р(11000)= 1000− 410 = 0, 59; Р(12000)= 1000− 450 = 0, 55
Р(11000)= 1000− 410 = 0, 59; Р(12000)= 1000− 450 = 0, 55
|
|
|
1000 1000

 Р(13000)= 1000− 500 = 0, 5; Р(14000)= 1000− 540 = 0, 46;
Р(13000)= 1000− 500 = 0, 5; Р(14000)= 1000− 540 = 0, 46;
1000 1000

 Р(15000) = 1000− 590 = 0, 41; Р(16000) = 1000− 630 = 0, 37;
Р(15000) = 1000− 590 = 0, 41; Р(16000) = 1000− 630 = 0, 37;
1000 1000

 Р(17000) = 1000− 680 = 0, 32; Р(18000) = 1000− 720 = 0, 28;
Р(17000) = 1000− 680 = 0, 32; Р(18000) = 1000− 720 = 0, 28;
1000 1000

 Р(19000) = 1000− 770 =0, 23; Р( 20000) = 1000− 805 = 0, 19;
Р(19000) = 1000− 770 =0, 23; Р( 20000) = 1000− 805 = 0, 19;
1000 1000

 Р( 21000) = 1000− 840 = 0, 16; Р(22000 ) = 1000− 890 = 0, 11;
Р( 21000) = 1000− 840 = 0, 16; Р(22000 ) = 1000− 890 = 0, 11;
1000 1000

 Р(23000) = 1000− 925 = 0, 075; Р( 24000) = 1000− 950 = 0, 05
Р(23000) = 1000− 925 = 0, 075; Р( 24000) = 1000− 950 = 0, 05
1000 1000

 Р( 25000) = 1000− 980 =0, 02; Р( 26000) = 1000− 1000 = 0
Р( 25000) = 1000− 980 =0, 02; Р( 26000) = 1000− 1000 = 0
Найдем частоту отказов по формуле:
 f(t)= n(Δ t)
f(t)= n(Δ t)
N0·Δ t
 f(500)= 20
f(500)= 20
1000 ·1000
 f(2500)= 35
f(2500)= 35
= 0, 2·10-4; f(1500)= 25 1000 ·1000

 = 0, 35·10-4; f(3500)= 50
= 0, 35·10-4; f(3500)= 50
= 0, 25·10-4;
= 0, 5·10-4;
1000 ·1000
 f(6500)= 40
f(6500)= 40
1000 ·1000
 f(8500)= 50
f(8500)= 50
1000 ·1000
 f(10500)= 40
f(10500)= 40
1000 ·1000
 = 0, 4·10-4; f(7500)= 40 1000 ·1000
= 0, 4·10-4; f(7500)= 40 1000 ·1000
 = 0, 5·10-4; f(9500)= 30 1000 ·1000
= 0, 5·10-4; f(9500)= 30 1000 ·1000
 = 0, 4·10-4; f(11500)= 40
= 0, 4·10-4; f(11500)= 40
= 0, 4·10-4;
= 0, 3·10-4;
= 0, 4·10-4;
1000 ·1000
 f(12500)= 50
f(12500)= 50
1000 ·1000
 f(14500)= 50
f(14500)= 50
1000 ·1000
1000 ·1000
 = 0, 5·10-4; f(13500)= 40 1000 ·1000
= 0, 5·10-4; f(13500)= 40 1000 ·1000
 = 0, 5·10-4; f(15500)= 40 1000 ·1000
= 0, 5·10-4; f(15500)= 40 1000 ·1000
= 0, 4·10-4;
= 0, 4·10-4;
 f(16500)= 50
f(16500)= 50
1000 ·1000
= 0, 5·10-4; f(17500)= 40 1000 ·1000
= 0, 4·10-4;

 f(18500)= 50 = 0, 5·10-4; f(19500)= 35 = 0, 35·10-4;
f(18500)= 50 = 0, 5·10-4; f(19500)= 35 = 0, 35·10-4;
1000 ·1000
 f(20500)= 35
f(20500)= 35
1000 ·1000
 f(22500)= 35
f(22500)= 35
1000 ·1000
 f(24500)= 30
f(24500)= 30
1000 ·1000
1000 ·1000
 =0, 35·10-4; f(21500)= 50
=0, 35·10-4; f(21500)= 50
1000 ·1000
 = 0, 35·10-4; f(23500)= 25
= 0, 35·10-4; f(23500)= 25
1000 ·1000
 = 0, 3·10-4; f(25500)= 20 1000 ·1000
= 0, 3·10-4; f(25500)= 20 1000 ·1000
= 0, 5·10-4;
= 0, 25·10-4;
= 0, 2·10-4.
Найдем интенсивность отказов по формуле:
|
|
|
 λ (t) = n(Δ t)
λ (t) = n(Δ t)
Δ t∙ 𝑁 ср
 λ (500) = 20
λ (500) = 20
 1000 · 1000 +980
1000 · 1000 +980
 λ (2500) = 35
λ (2500) = 35
 1000 · 955 +920
1000 · 955 +920
 λ (4500) = 30
λ (4500) = 30
 1000 · 870 +840
1000 · 870 +840
 λ (6500) = 40
λ (6500) = 40
 1000 · 790 +750
1000 · 790 +750
 λ (8500) = 50
λ (8500) = 50
 1000 · 710 +660
1000 · 710 +660
 λ (10500) = 40
λ (10500) = 40
=0, 20·10-4; λ (1500) = 25

 1000 · 980 +955
1000 · 980 +955
 = 0, 37·10-4; λ (3500) = 50
= 0, 37·10-4; λ (3500) = 50
 1000 · 920 +870
1000 · 920 +870
 = 0, 35·10-4; λ (5500) = 50
= 0, 35·10-4; λ (5500) = 50
 1000 · 840 +790
1000 · 840 +790
 = 0, 52·10-4; λ (7500) = 40
= 0, 52·10-4; λ (7500) = 40
 1000 · 750 +710
1000 · 750 +710
 = 0, 73·10-4; λ (9500) = 30
= 0, 73·10-4; λ (9500) = 30
 1000 · 660 +630
1000 · 660 +630
 = 0, 65·10-4; λ (11500) = 40
= 0, 65·10-4; λ (11500) = 40
= 0, 26·10-4;
= 0, 56·10-4;
= 0, 61·10-4;
= 0, 55·10-4;
= 0, 46·10-4;
= 0, 69·10-4;
 1000 · 630 +600
1000 · 630 +600
 λ (12500) = 50
λ (12500) = 50
 1000 · 560 +510
1000 · 560 +510
 λ (14500) = 50
λ (14500) = 50
 1000 · 470 +420
1000 · 470 +420
1000 · 600 +560
 2
2
 = 0, 93·10-4; λ (13500) = 40
= 0, 93·10-4; λ (13500) = 40
 1000 · 510 +470
1000 · 510 +470
 = 1, 12·10-4; λ (15500) = 40
= 1, 12·10-4; λ (15500) = 40
 1000 · 420 +380
1000 · 420 +380
= 0, 82·10-4;
= 1·10-4;
 λ (16500) = 50
λ (16500) = 50
 1000 · 380 +330
1000 · 380 +330
 λ (18500) = 50
λ (18500) = 50
 1000 · 290 +240
1000 · 290 +240
 λ (20500) = 35
λ (20500) = 35
 1000 · 205 +170
1000 · 205 +170
= 1, 41·10-4; λ (17500) = 40

 1000 · 330 +290
1000 · 330 +290
 = 1, 88·10-4; λ (19500) = 35
= 1, 88·10-4; λ (19500) = 35
 1000 · 240 +205
1000 · 240 +205
 = 1, 87·10-4; λ (21500) = 50
= 1, 87·10-4; λ (21500) = 50
 1000 · 170 +120
1000 · 170 +120
= 1, 29·10-4;
= 1, 57·10-4;
= 3, 45·10-4;
 λ (22500) = 35
λ (22500) = 35
 1000 · 120 +85
1000 · 120 +85
= 3, 41·10-4; λ (23500) = 25

 1000 · 85+60
1000 · 85+60
= 3, 45·10-4;
 λ (24500) = 30
λ (24500) = 30
 1000 · 60+30
1000 · 60+30
= 6, 67·10-4; λ (25500) = 20

 1000 · 30+20
1000 · 30+20
= 8·10-4;
Значения Р(t), f(t), λ (t), вычисленные для всех Δ ti.
| Δ ti, ч | Р(t) | f(t), ·10-4ч | λ (t), ·10-4ч |
| 0-1000 | 0, 98 | 0, 20 | 0, 20 |
| 1000-2000 | 0, 955 | 0, 25 | 0, 26 |
| 2000-3000 | 0, 92 | 0, 35 | 0, 37 |
| 3000-4000 | 0, 87 | 0, 50 | 0, 56 |
| 4000-5000 | 0, 84 | 0, 30 | 0, 35 |
| 5000-6000 | 0, 79 | 0, 50 | 0, 61 |
| 6000-7000 | 0, 75 | 0, 40 | 0, 52 |
| 7000-8000 | 0, 71 | 0, 40 | 0, 55 |
| 8000-9000 | 0, 66 | 0, 50 | 0, 73 |
| 9000-10000 | 0, 63 | 0, 30 | 0, 46 |
| 10000-11000 | 0, 59 | 0, 40 | 0, 65 |
| 11000-12000 | 0, 55 | 0, 40 | 0, 69 |
| 12000-13000 | 0, 50 | 0, 50 | 0, 93 |
| 13000-14000 | 0, 46 | 0, 40 | 0, 82 |
| 14000-15000 | 0, 41 | 0, 50 | 1, 12 |
| 15000-16000 | 0, 37 | 0, 40 | |
| 16000-17000 | 0, 32 | 0, 50 | 1, 41 |
| 17000-18000 | 0, 28 | 0, 40 | 1, 29 |
| 18000-19000 | 0, 23 | 0, 50 | 1, 88 |
| 19000-20000 | 0, 195 | 0, 35 | 1, 57 |
| 20000-21000 | 0, 16 | 0, 35 | 1, 87 |
| 21000-22000 | 0, 11 | 0, 50 | 3, 45 |
| 22000-23000 | 0, 075 | 0, 35 | 3, 41 |
| 23000-24000 | 0, 05 | 0, 25 | 3, 45 |
| 24000-25000 | 0, 02 | 0, 30 | 6, 67 |
| 25000-26000 | 0, 20 |
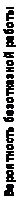 1. 2
1. 2
0. 8
0. 6
0. 4
0. 2
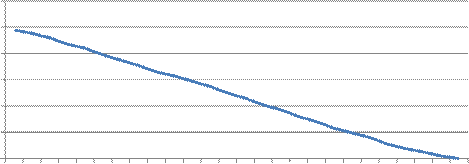
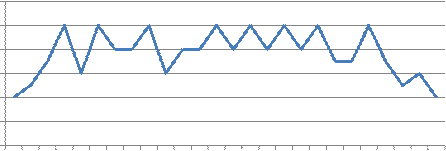
Вероятность безотказной работы от времени - Р

 Кол - во часов работы
Кол - во часов работы
Частота отказов от времени, f
 0. 00006
0. 00006
 0. 00005
0. 00005
0. 00004
0. 00003
0. 00002
0. 00001
 0
0
Кол-во часов работы
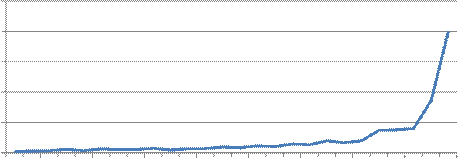
Интенсивность отказов от времени, λ
 0. 0025000
0. 0025000
 0. 0020000
0. 0020000
0. 0015000
|
|
|
0. 0010000
0. 0005000
 0. 0000000
0. 0000000
Кол-во часов работы
Найдем среднюю наработку до первого отказа:
m = tk
= 26000 = 26; N
= 1000

 Δ t
Δ t
𝑚
𝑛 𝑖 ∙ 𝑡 ср 𝑖
 12925000
12925000
Tср= 𝑖 =1 =
N0
= 12925
Tср= 12925
Вывод: Вероятность безотказной работы с увеличением количества часов работы падает линейно на всех промежутках времени. Частота отказов в начале испытания составила 0, 2 · 10-4. Далее в процессе испытаний частота отказов выросла и держалась в пределах 0, 35·10-4 – 0, 5 · 10-4. В конце испытания частота отказов понизилась до
0, 2·10-4
Интенсивность отказов в процессе испытания увеличивалась экспоненциально незначительно. После 20500 часов работы интенсивность отказов резко увеличилась экспоненциально.
Пример 27
В результате наблюдений за 45 образцами радиоэлектронного оборудования получены данные до первого отказа всех 45 образцов. Определить: Р(t); f(t); λ (t) в функции времени, построить графики этих функций, а также найти среднюю наработку до первого отказа (Tср).
| Δ ti, ч | n(Δ ti) | Δ ti, ч | n(Δ ti) |
| 0-5 | 40-45 | ||
| 5-10 | 45-50 |
| 10-15 | 50-55 | ||
| 15-20 | 55-60 | ||
| 20-25 | 60-65 | ||
| 25-30 | 65-70 | ||
| 30-35 | 70-75 | ||
| 35-40 | 75-80 |
 Решение:
Решение:
Определим вероятность безотказной работы по формуле:
Р(t)= 𝑁 0 − 𝑛 (𝑡 );
𝑁 0


 Р(5) = 45− 1 = 0, 98; Р(10) = 45− 6 = 0, 87; Р(15) = 45− 14 = 0, 69;
Р(5) = 45− 1 = 0, 98; Р(10) = 45− 6 = 0, 87; Р(15) = 45− 14 = 0, 69;
45 45 45


 Р(20) = 45− 16 = 0, 64; Р(25) = 45− 21 = 0, 53; Р(30) = 45− 27 = 0, 4;
Р(20) = 45− 16 = 0, 64; Р(25) = 45− 21 = 0, 53; Р(30) = 45− 27 = 0, 4;
45 45 45


 Р(35) = 45− 31 = 0, 31; Р(40) = 45− 34 = 0, 24; Р(45) = 45− 34 = 0. 24;
Р(35) = 45− 31 = 0, 31; Р(40) = 45− 34 = 0, 24; Р(45) = 45− 34 = 0. 24;
45 45 45


 Р(50) = 45− 35 = 0, 22; Р(55) = 45− 35 = 0. 22; Р(60) = 45− 35 = 0. 22;
Р(50) = 45− 35 = 0, 22; Р(55) = 45− 35 = 0. 22; Р(60) = 45− 35 = 0. 22;
45 45 45


 Р(65) = 45− 38 = 0, 16; Р(70) = 45− 41 = 0, 09; Р(75) = 45− 44 = 0, 02;
Р(65) = 45− 38 = 0, 16; Р(70) = 45− 41 = 0, 09; Р(75) = 45− 44 = 0, 02;
|
|
|
45 45 45
 Р(80) = 45− 45 =0.
Р(80) = 45− 45 =0.
Найдем частоту отказов по формуле:
 f(t)= n(Δ t)
f(t)= n(Δ t)
N0·Δ t
 f(2, 5)= 1
f(2, 5)= 1
45·5
 f(17, 5)= 2
f(17, 5)= 2
= 0, 44·10-2; f(7, 5)= 5
 45·5
45·5
 = 0, 88·10-2; f(22, 5)= 5
= 0, 88·10-2; f(22, 5)= 5
= 2, 22·10-2; f(12, 5)= 8
 45·5
45·5
 = 2, 22·10-2; f(27, 5)= 6
= 2, 22·10-2; f(27, 5)= 6
= 3, 55·10-2;
= 2, 66·10-2
45·5
 f(32, 5)= 4
f(32, 5)= 4
45·5
45·5
 = 1, 77·10-2; f(37, 5)= 3
= 1, 77·10-2; f(37, 5)= 3
45·5
45·5
= 1, 33·10-2; f(42, 5)= 0;
 f(47, 5)= 1
f(47, 5)= 1
45·5
= 0, 44·10-2; f(52, 5)= 0; f(57, 5)= 0; f(62, 5)= 3
 45·5
45·5
= 1, 33·10-2;
 f(67, 5)= 3
f(67, 5)= 3
45·5
= 1, 33·10-2; f(72, 5)= 3
 45·5
45·5
= 1, 33·10-2; f(77, 5)= 1
 45·5
45·5
= 0, 44·10-2.
Найдем интенсивность отказов по формуле:
 λ (t) = n(Δ t)
λ (t) = n(Δ t)
Δ t∙ 𝑁 ср
 λ (2, 5) = 1
λ (2, 5) = 1
 5· 45+44
5· 45+44
 λ (12, 5) = 8
λ (12, 5) = 8
= 0, 45·10-2; λ (7, 5) = 5

 5· 44+39
5· 44+39
 = 4, 57·10-3; λ (17, 5) = 2
= 4, 57·10-3; λ (17, 5) = 2
= 2, 40·10-3;
=1, 33·10-2;
| |
| |
· 2
31+29
· 2


|
|
=5, 71·10-2;

 5· 2 5· 2
5· 2 5· 2


|
|
= 4, 8·10-2;

 5· 2 5· 2
5· 2 5· 2

|
 5· 2
5· 2


|
|
= 10, 9·10-2;

 5· 2 5· 2
5· 2 5· 2


|
|
= 40·10-2.

 5· 2 5· 2
5· 2 5· 2
Значения Р(t), f(t), λ (t), вычисленные для всех Δ ti.
| Δ ti, ч | Р(t) | α (t), ·10-2ч | λ (t), ·10-2ч |
| 0-5 | 0, 98 | 0, 44 | 0, 45 |
| 5-10 | 0, 87 | 2, 22 | 2, 40 |
| 10-15 | 0, 69 | 3, 55 | 4, 57 |
| 15-20 | 0, 64 | 0, 88 | 1, 33 |
| 20-25 | 0, 53 | 2, 22 | 3, 77 |
| 25-30 | 0, 4 | 2, 66 | 5, 71 |
| 30-35 | 0, 31 | 1, 77 | |
| 35-40 | 0, 24 | 1, 33 | 4, 8 |
| 40-45 | 0, 24 | ||
| 45-50 | 0, 22 | 0, 44 | 1, 90 |
| 50-55 | 0, 22 | ||
| 55-60 | 0, 22 | ||
| 60-65 | 0, 16 | 1, 33 | 7, 05 |
| 65-70 | 0, 09 | 1, 33 | 10, 9 |
| 70-75 | 0, 02 | 1, 33 | |
| 75-80 | 0, 44 |
Tcp
 |
å nitcpi
= i=1 =
N0
Находим среднюю наработку до первого отказа.
Учитывая, что в данном случае: m=tk/Δ t=80/5=16;
N0=45;
имеем:
1* 2. 5 + 5 * 7. 5 + 8 *12. 5 + 2 *17. 5 +... + 3* 62. 5 + 3* 67. 5 + 3* 72. 5 +1* 77. 5

= 31. 72
1. 20
Вероятность безотказной работы от
 времени - Р
времени - Р
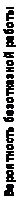 1. 00
1. 00
0. 80
|
|
|
0. 60
0. 40
0. 20
 0. 00
0. 00

 Кол - во часов работы
Кол - во часов работы
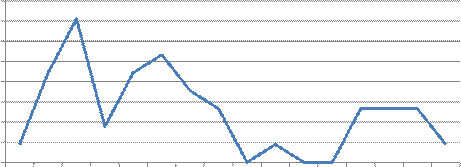
Частота отказов от времени, f
 0. 040
0. 040
0. 035
 0. 030
0. 030
0. 025
0. 020
0. 015
0. 010
0. 005

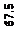
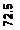
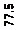 0. 000
0. 000
Кол-во часов работы
Интенсивность отказов от времени, λ
 0. 4500
0. 4500
 0. 4000
0. 4000
0. 3500
0. 3000
0. 2500
0. 2000
0. 1500
0. 1000
0. 0500

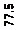 0. 0000
0. 0000
Кол-во часов работы
Вывод. Вероятность безотказной работы на всем процессе наблюдения уменьшается, а в промежутке наблюдения от 40 до 60 часов работы остановилась на уровне 0, 22.
В промежутке времени от 2, 5 до 12, 5 часов работы частота отказов увеличивалась и достигла 36 · 10-3 ч. В промежутке от 12, 5 до 17, 5 часов частота отказов уменьшилась до 9 · 10-3 ч. В промежутке от 17, 5 до 27, 5 часов частота отказов увеличилась до 27 · 10-3 ч. В промежутке от 27, 5 до 42, 5 часов падает до нуля. В промежутке от 42, 5 до 57, 5 ч частота отказов не превышает 5·10-3 ч и после 47, 5 часов работы падает до нуля. В промежутке от 57, 5 до 62, 5 часов работы частота отказов увеличилась до 13 · 10-3 ч и держалась до 72, 5 часов работы наблюдений. В конце испытания частота отказов упала до 4·10-3 ч.
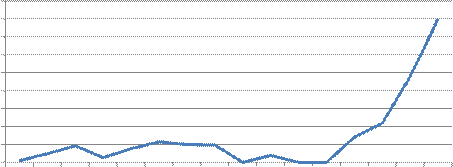
В процессе наблюдения от 2, 5 до 57, 5 часов интенсивность отказов была в пределах от 0 до 5, 71·10-2 ч. После 57, 5 часов работы наблюдений интенсивность отказов резко увеличилась и в конце наблюдения достигла 0, 4 ч.
Пример 28
В результате наблюдений за 45 образцами радиоэлектронного оборудования, которые прошли предварительную 80-часовую приработку, получены данные до первого отказа всех 45 образцов. Требуется определить: Р(t); f(t); λ (t) в функции времени, построить графики этих функций, а также найти среднюю наработку до первого отказа (Tср).
| Δ ti, ч | n(Δ ti) |
| 0 – 10 | |
| 10 – 20 | |
| 20 – 30 | |
| 30 – 40 | |
| 40 – 50 | |
| 50 – 60 | |
| 60 – 70 |
Решение:
Вычислим Р(t) по формуле:
 P(t) = (N 0 - n(t))
P(t) = (N 0 - n(t))
N 0
 P(10) = 45 -19 = 0, 58;
P(10) = 45 -19 = 0, 58;
 P(40) = 45 - 43 = 0, 04;
P(40) = 45 - 43 = 0, 04;
P(20) = 45 - 32 = 0, 29;
 45
45
 P(50) = 45 - 43 = 0, 04;
P(50) = 45 - 43 = 0, 04;
 P(70) = 45 - 45 = 0
P(70) = 45 - 45 = 0
P(30) = 45 - 40 = 0, 11;
 45
45
 P(60) = 45 - 44 = 0, 02;
P(60) = 45 - 44 = 0, 02;
Рассчитываем частоту отказов по формуле:
 f (t) = n(Dt)
f (t) = n(Dt)
N0Dt
f (5) =

45× 10
= 0, 042;
f (15) =

45× 10
= 0, 029;
f (25) =

45× 10
= 0, 018;
f (35) =

45× 10
= 0, 007;
f (45) =
f (65) =

45× 10
 45× 10
45× 10
= 0;
= 0, 002;
f (55) =

45× 10
= 0, 002;
Рассчитываем интенсивность отказов по формуле:
l(5) =

10 × æ 45 + 26 ö
l(t) =
= 0, 0535;
n(Dt)

Ncp Dt
l(15) =

10 × æ 26 +13 ö
= 0, 0667;
ç 2 ÷ ç 2 ÷
l(25) =
è ø

10 × æ 13 + 5 ö
= 0, 0889;
l(35) =
è ø

10 × æ 5 + 2 ö
= 0, 0857;
ç 2 ÷ ç 2 ÷
è ø è ø
l(45) =

10 × æ 2 + 2 ö
= 0;
l(55) =

10 × æ 2 +1 ö
= 0, 0667;
ç 2 ÷ ç 2 ÷
è ø
l(65) =

10 × æ 1+ 0 ö
è ø
= 0, 2;
ç 2 ÷
è ø
Значения P(t), α (t), λ (t), вычисленные для всех Δ ti сведем в таблицу:
| Δ ti, ч | P(t) | α (t), ч | λ (t), ч |
| 0 – 10 | 0, 58 | 0, 042 | 0, 0535 |
| 10 – 20 | 0, 29 | 0, 029 | 0, 0667 |
| 20 – 30 | 0, 11 | 0, 018 | 0, 0889 |
| 30 – 40 | 0, 04 | 0, 007 | 0, 0857 |
| 40 – 50 | 0, 04 | ||
| 50 – 60 | 0, 02 | 0, 002 | 0, 0667 |
| 60 – 70 | 0, 002 | 0, 2 |
Находим среднюю наработку до первого отказа.
Учитывая, что в данном случае: m=tk/Δ t=70/10=7;
N0=45;
имеем:
å nitcpi
19* 5 +13*15 + 8 * 25 + 3* 35 + 0 * 45 +1* 55 +1* 65
Tcp
= i=1 =
N0
= 15. 89
 45
45
Строим графики функций.
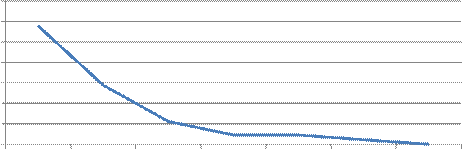
 0. 70
0. 70
0. 60
0. 50
0. 40
0. 30
0. 20
0. 10
0. 00
|
|
|


