 |
Тема: Решение задач по теме «Геометрические преобразования в пространстве»
|
|
|
|
13. 10. 2021г.
Тема: Решение задач по теме «Геометрические преобразования в пространстве»
Прочитать и переписать примеры с чертежами выделенные красным цветом.
Содержание:
1. Движение (перемещение) фигуры. Параллельный перенос
1. Что такое преобразование фигур
1. Пример №1
2. Пример №2
3. Пример №3
2. Осевая симметрия
1. Пример №4
2. Пример №5
3. Центральная симметрия. Поворот
1. Пример №6
2. Пример №7
3. Пример №8
4. Пример №9
4. Подобие фигур
1. Пример №10
2. Пример №11
3. Пример №12
5. Применение преобразований фигур при решении задач
1. Пример №13
2. Пример №14
3. Пример №15
4. Пример №16
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17. 1 изображены отрезок 
Мы указали правило, с помощью которого каждой точке 
отрезка 
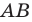поставлена в соответствие единственная точка 
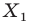отрезка 
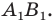В этом случае говорят, что отрезок 
получен в результате преобразования отрезка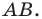 
Пример:
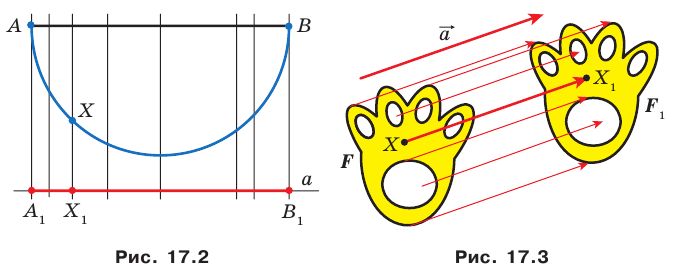
На рисунке 17. 2 изображены полуокружность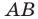 
и прямая 
параллельная диаметру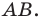 
Каждой точке 
полуокружности поставим в соответствие точку 
прямой а так, чтобы прямая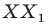 
была перпендикулярна прямой 
Понятно, что все такие точки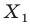 
образуют отрезок 
В этом случае говорят, что отрезок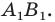 
получен в результате преобразования полуокружности 
Пример:
Пусть даны некоторая фигура 
и вектор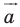 
(рис. 17. 3). Каждой точке 
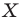фигуры 
поставим в соответствие точку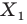 
такую, что 
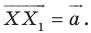В результате такого преобразования фигуры 
получим фигуру 
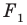(рис. 17. 3). Такое преобразование фигуры 
называют параллельным переносом на вектор 
|
|
|
Обобщим приведенные примеры.
Пусть задана некоторая фигура 
Каждой точке фигуры 
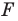поставим в соответствие (сопоставим) по определенному правилу некоторую точку. Все полученные сопоставленные точки образуют фигуру 
Говорят, что фигура
получена в результате преобразования фигуры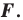 
При этом фигуру 
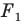называют образом фигуры 
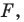а фигуру 
— прообразом фигуры 
Так, в примере 1 отрезок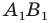 
является образом отрезка 
Точка 
является образом точки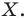 
Отрезок 
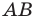— это прообраз отрезка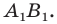 
Обратим внимание на то, что в примере 3 фигура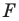 
равна своему образу 
Преобразования, описанные в примерах 1 и 2, таким свойством не обладают.
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 
— произвольные точки фигуры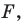 
а точки 
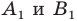— их образы, то должно выполняться равенство 
Что такое преобразование фигур
Определение. Преобразование фигуры 
сохраняющее расстояние между точками, называют движением (перемещением) фигуры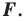 
Если каждой точке 
фигуры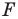 
поставлена в соответствие эта же точка 
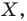то такое преобразование фигуры 
называют тождественным. При тождественном преобразовании образом фигуры 
является сама фигура . Очевидно, что тождественное преобразование является движением.
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
|
|
|
Свойства движения подсказывают следующее определение.
|
|
|
