 |
Центральная симметрия. Поворот
|
|
|
|
Центральная симметрия. Поворот
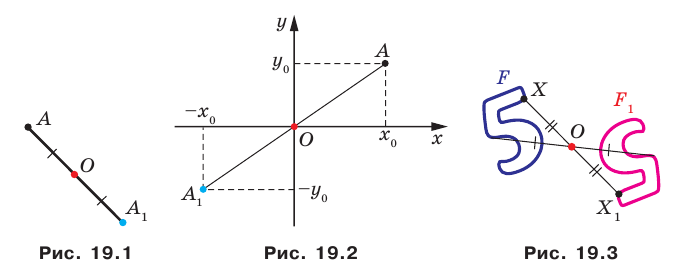
Определение. Точкиназывают симметричными относительно точкиесли точкаявляется серединой отрезка(рис. 19. 1). Точкусчитают симметричной самой себе.
 Например, точки
Например, точки 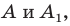 у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19. 2).
у которых как абсциссы, так и ординаты — противоположные числа, симметричны относительно начала координат (рис. 19. 2).
Рассмотрим фигуру 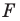 и точку
и точку  Каждой точке
Каждой точке  фигуры
фигуры  поставим в соответствие симметричную ей относительно точки
поставим в соответствие симметричную ей относительно точки 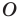 точку
точку 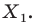 В результате такого преобразования фигуры
В результате такого преобразования фигуры  получим фигуру
получим фигуру  (рис. 19. 3). Такое преобразование фигуры
(рис. 19. 3). Такое преобразование фигуры  называют центральной симметрией относительно точки
называют центральной симметрией относительно точки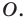 Точку
Точку 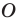 называют центром симметрии. Также говорят, что фигуры
называют центром симметрии. Также говорят, что фигуры 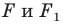 симметричны относительно точки
симметричны относительно точки
Теорема 19. 1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 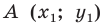 и
и 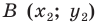 — произвольные точки фигуры
— произвольные точки фигуры  Точки
Точки 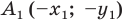 и
и 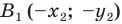 — соответственно их образы при центральной симметрии относительно начала координат. Имеем:
— соответственно их образы при центральной симметрии относительно начала координат. Имеем: 
Мы получили, что 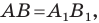 то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением.
то есть центральная симметрия сохраняет расстояние между точками. Следовательно, центральная симметрия является движением. 
Следствие. Если фигуры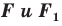 симметричны относительно точки, то
симметричны относительно точки, то
Определение. Фигуру называют симметричной относительно точкиесли для каждой точки данной фигуры точка, симметричная ей относительно точкитакже принадлежит этой фигуре.
Точку  называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
называют центром симметрии фигуры. Также говорят, что фигура имеет центр симметрии.
Приведем примеры фигур, имеющих центр симметрии.
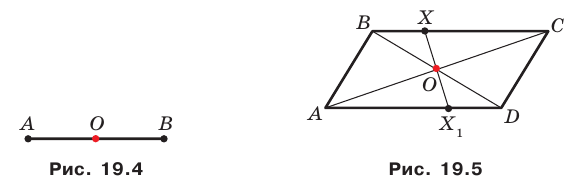
Центром симметрии отрезка является его середина (рис. 19. 4).
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19. 5).
|
|
|
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19. 6).

Пример №6
Докажите, что образом данной прямой 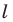 при симметрии относительно точки
при симметрии относительно точки 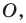 не принадлежащей прямой
не принадлежащей прямой 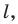 является прямая, параллельная данной.
является прямая, параллельная данной.
Решение:
Поскольку центральная симметрия — это движение, то образом прямой  будет прямая. Для построения прямой достаточно найти две любые ее точки.
будет прямая. Для построения прямой достаточно найти две любые ее точки.
Выберем на прямой  произвольные точки
произвольные точки  (рис. 19. 7). Пусть точки
(рис. 19. 7). Пусть точки  — их образы при центральной симметрии относительно точки
— их образы при центральной симметрии относительно точки  Тогда прямая
Тогда прямая  — образ прямой
— образ прямой 
Поскольку  углы
углы  равны как вертикальные, то треугольники
равны как вертикальные, то треугольники  равны по первому признаку равенства треугольников. Отсюда
равны по первому признаку равенства треугольников. Отсюда  (рис. 19. 7). Следовательно, по признаку параллельных прямых
(рис. 19. 7). Следовательно, по признаку параллельных прямых 
Пример №7
Точка 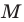 принадлежит углу
принадлежит углу  (рис. 19. 8). На сторонах
(рис. 19. 8). На сторонах  угла постройте такие точки
угла постройте такие точки  чтобы точка
чтобы точка 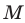 была серединой отрезка
была серединой отрезка 
Решение:
Пусть прямая 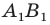 — образ прямой
— образ прямой 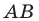 при центральной симметрии относительно точки
при центральной симметрии относительно точки  (рис. 19. 9). Обозначим буквой
(рис. 19. 9). Обозначим буквой 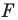 точку пересечения прямых
точку пересечения прямых 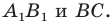
Найдем прообраз точки 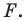 Очевидно, что он лежит на прямой
Очевидно, что он лежит на прямой  Поэтому достаточно найти точку пересечения прямых
Поэтому достаточно найти точку пересечения прямых 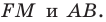
Обозначим эту точку буквой  Тогда
Тогда  — искомые точки.
— искомые точки. 

Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19. 10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота». 
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19. 11).


На рисунке 19. 12 изображены точки  такие, что
такие, что 
|
|
|
Говорят, что точка  является образом точки
является образом точки 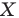 при повороте вокруг центра
при повороте вокруг центра против часовой стрелки на угол
против часовой стрелки на угол 
Так же говорят, что точка  — это образ точки
— это образ точки  при повороте вокруг центра
при повороте вокруг центра по часовой стрелке на угол
по часовой стрелке на угол 
Точку  называют центром поворота, угол
называют центром поворота, угол 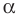 — углом поворота.
— углом поворота.
Рассмотрим фигуру  точку
точку  и угол
и угол  Каждой точке
Каждой точке 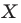 фигуры
фигуры  поставим в соответствие точку
поставим в соответствие точку  являющуюся образом точки
являющуюся образом точки  при повороте вокруг центра
при повороте вокруг центра 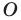 против часовой стрелки на угол
против часовой стрелки на угол  (если точка
(если точка  принадлежит фигуре
принадлежит фигуре  то ей сопоставляется она сама). В результате такого преобразования фигуры
то ей сопоставляется она сама). В результате такого преобразования фигуры 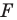 получим фигуру
получим фигуру 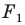 (рис. 19. 13). Такое преобразование фигуры
(рис. 19. 13). Такое преобразование фигуры  называют поворотом вокруг центра
называют поворотом вокруг центра против часовой стрелки на угол
против часовой стрелки на угол  Точку
Точку 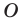 называют центром поворота.
называют центром поворота. 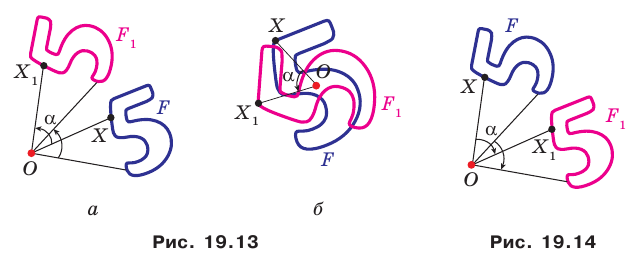
Аналогично определяют преобразование поворота фигуры 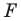 по часовой стрелке на угол
по часовой стрелке на угол 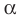 (рис. 19. 14).
(рис. 19. 14).
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол 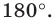
Теорема 19. 2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура  — образ фигуры
— образ фигуры 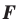 при повороте, то
при повороте, то 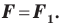
|
|
|


