 |
Осевая симметрия. Определение. Фигуру называют симметричной относительно прямойесли для каждой точки данной фигуры точка, симметричная ей относительно прямойтакже принадлежит этой фигуре.
|
|
|
|
Осевая симметрия
Определение. Точки называют симметричными относительно прямой
называют симметричными относительно прямой  если прямая
если прямая  является серединным перпендикуляром отрезка
является серединным перпендикуляром отрезка 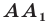 (рис. 18. 1). Если точка
(рис. 18. 1). Если точка  принадлежит прямой
принадлежит прямой  то ее считают симметричной самой себе относительно прямой
то ее считают симметричной самой себе относительно прямой 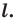
Например, точки  у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18. 2).
у которых ординаты равны, а абсциссы — противоположные числа, симметричны относительно оси ординат (рис. 18. 2).
Рассмотрим фигуру  и прямую
и прямую  Каждой точке
Каждой точке 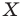 фигуры
фигуры 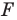 поставим в соответствие симметричную ей относительно прямой
поставим в соответствие симметричную ей относительно прямой 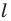 точку
точку 
В результате такого преобразования фигуры 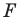 получим фигуру
получим фигуру  (рис. 18. 3). Такое преобразование фигуры
(рис. 18. 3). Такое преобразование фигуры 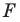 называют осевой симметрией относительно прямой
называют осевой симметрией относительно прямой Прямую
Прямую 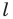 называют осью симметрии. Говорят, что фигуры
называют осью симметрии. Говорят, что фигуры  симметричны относительно прямой
симметричны относительно прямой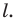


Теорема 18. 1 (свойство осевой симметрии). Осевая симметрия является движением.
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть  и
и  — произвольные точки фигуры
— произвольные точки фигуры  Тогда точки
Тогда точки 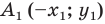 и
и  — их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
— их соответствующие образы при осевой симметрии относительно оси ординат. Имеем:
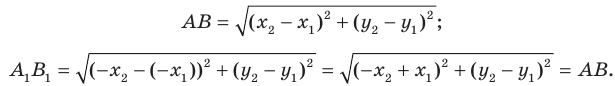
Мы получили, что  то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением.
то есть осевая симметрия сохраняет расстояние между точками. Следовательно, осевая симметрия является движением. 
Следствие. Если фигуры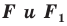 симметричны относительно прямой, то
симметричны относительно прямой, то
Определение. Фигуру называют симметричной относительно прямойесли для каждой точки данной фигуры точка, симметричная ей относительно прямойтакже принадлежит этой фигуре.
Прямую 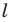 называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
называют осью симметрии фигуры. Также говорят, что фигура имеет ось симметрии.
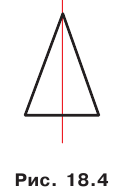
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18. 4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
|
|
|
Любой угол имеет ось симметрии — это пря-Рис. 18. 5 мая, содержащая его биссектрису (рис. 18. 5). 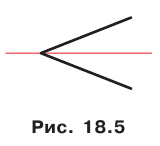
Равносторонний треугольник имеет три оси симметрии (рис. 18. 6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18. 7).

Квадрат имеет четыре оси симметрии (рис. 18. 8).
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18. 9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник  Провели прямую
Провели прямую  содержащую биссектрису угла
содержащую биссектрису угла  Потом рисунок стерли, оставив только точки
Потом рисунок стерли, оставив только точки  и прямую
и прямую 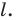 Восстановите треугольник
Восстановите треугольник 
Решение:
Поскольку прямая 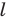 является осью симметрии угла
является осью симметрии угла  то точка
то точка  — образ точки
— образ точки  при симметрии относительно прямой
при симметрии относительно прямой  — принадлежит лучу
— принадлежит лучу 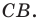 Тогда пересечением прямых
Тогда пересечением прямых 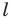 и
и 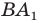 является вершина
является вершина  искомого треугольника
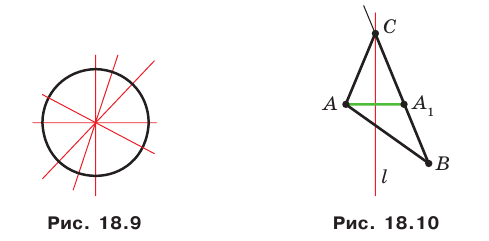
искомого треугольника  (рис. 18. 10).
(рис. 18. 10).
Эти соображения подсказывают, как построить искомый треугольник: строим точку  симметричную точке
симметричную точке  относительно прямой
относительно прямой 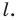 Находим вершину
Находим вершину 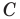 как точку пересечения прямых
как точку пересечения прямых 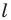 и
и 
Пример №5
Точка 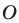 принадлежит острому углу
принадлежит острому углу  (рис. 18. 11). На сторонах
(рис. 18. 11). На сторонах  угла найдите такие точки
угла найдите такие точки  чтобы периметр треугольника
чтобы периметр треугольника 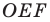 был наименьшим.
был наименьшим.
Решение:
Пусть точки  — образы точки
— образы точки  при симметриях относительно прямых
при симметриях относительно прямых 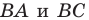 соответственно (рис. 18. 12), а прямая
соответственно (рис. 18. 12), а прямая  пересекает стороны
пересекает стороны 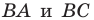 в точках
в точках  соответственно. Докажем, что точки
соответственно. Докажем, что точки  — искомые.
— искомые.

Заметим, что отрезки  симметричны относительно прямой
симметричны относительно прямой 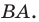 Следовательно,
Следовательно, 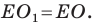 Аналогично
Аналогично  Тогда периметр треугольника
Тогда периметр треугольника  равен длине отрезка
равен длине отрезка 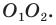
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 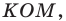 где
где 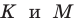 — произвольные точки соответственно лучей
— произвольные точки соответственно лучей 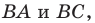 причем точка
причем точка  не совпадает с точкой
не совпадает с точкой 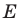 или точка
или точка  не совпадает с точкой
не совпадает с точкой 
|
|
|
Понятно, что 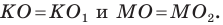
Тогда периметр треугольника  равен сумме
равен сумме 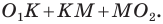 Однако
Однако 
|
|
|


