 |
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
|
|
|
|
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20. 8. 
Запись 
означает, что фигуры 
подобны. Также говорят, что фигура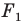 
— образ фигуры 
при преобразовании подобия.
Из приведенного определения следует, что при преобразовании подобия фигуры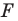 
расстояния между ее точками изменяются в одно и то же количество раз.
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20. 8, следует, что гомотетия — частный случай преобразования подобия.
Пусть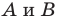 
— произвольные точки фигуры 
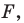а точки 
— их образы при преобразовании подобия. Точки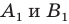 
принадлежат фигуре 
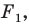которая подобна фигуре 
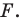Число 
называют коэффициентом подобия. Говорят, что фигура 
подобна фигуре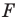 
с коэффициентом подобия 
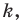а фигура 
подобна фигуре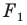 
с коэффициентом подобия 
Заметим, что преобразование подобия с коэффициентом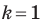 
является движением. Отсюда следует, что движение — частный случай преобразования подобия.
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20. 9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия.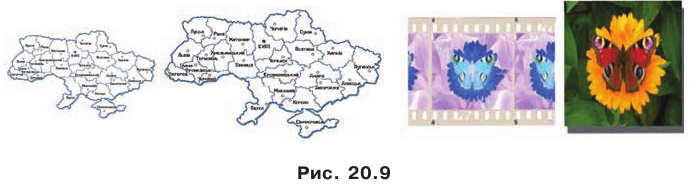 
Теорема 20. 2. Отношение площадей подобных многоугольников равно квадрату коэффициента подобия.
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
|
|
|
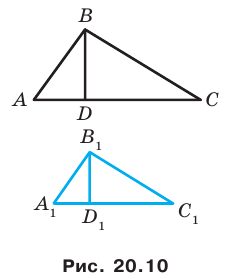
Доказательство: Пусть треугольник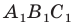 
— образ треугольника 
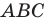при преобразовании подобия с коэффициентом 
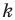(рис. 20. 10). Сторона 
— образ стороны 
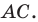Тогда 
Проведем высоту 
Пусть точка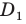 
— образ точки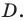 
Поскольку при преобразовании подобия сохраняются углы, то отрезок 
— высота треугольника 
Тогда 
Имеем:
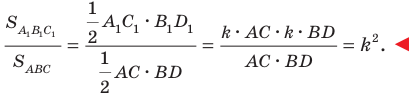
Пример №10
Докажите, что образом прямой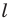 
при гомотетии с центром 
не принадлежащим прямой 
является прямая, параллельная данной.
Решение:
Из свойств гомотетии следует, что образом прямой 
будет прямая. Для построения прямой достаточно найти две любые ее точки. Выберем на прямой произвольные точки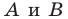 
(рис. 20. 11). Пусть точки 
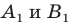— их образы при гомотетии с центром 
и коэффициентом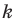 
(рисунок 20. 11 соответствует случаю, когда 
Тогда прямая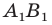 
— образ прямой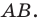 
При доказательстве теоремы 20. 1 мы показали, что 
Следовательно, 
Пример №11
В остроугольный треугольник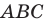 
впишите квадрат так, чтобы две его вершины лежали соответственно на сторонах 
и 
а две другие — на стороне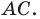 
Решение:
Из произвольной точки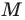 
стороны 
опустим перпендикуляр 
на сторону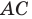 
(рис. 20. 12). Построим квадрат 
так, чтобы точка 
лежала на луче 
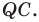Пусть луч 
пересекает сторону 
в точке 
Рассмотрим гомотетию с центром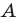 
и коэффициентом 
Тогда точка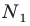 
образ точки 
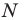при этой гомотетии. Образом отрезка 
является отрезок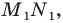 
где точка 
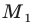принадлежит лучу 
причем 
Аналогично отрезок 
такой, что точка 
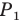принадлежит лучу 
является образом отрезка 
Следовательно, отрезки 
— соседние стороны искомого квадрата. Для завершения построения осталось опустить перпендикуляр 
на сторону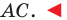 
|
|
|
