 |
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
|
|
|
|
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 
означает, что фигуры 
равны.
Если существует движение, при котором фигура 
является образом фигуры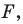 
то обязательно существует движение, при котором фигура 
является образом фигуры 
Такие движения называют взаимно обратными.
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 
на фигуру 
можно рассматривать как движение фигуры 
при котором ее образом будет фигура 
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17. 3 фигуры 
равны, понятно из наглядных соображений. Строгое обоснование этого факта дает следующая теорема.
Теорема 17. 1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 
— произвольные точки фигуры 
(рис. 17. 4), точки 
— их соответствующие образы при параллельном переносе на вектор 
Докажем, что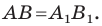 
Имеем: 
Векторы 
и 
имеют координаты 
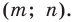Следовательно, координатами точек 
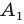и 
являются соответственно пары чисел 
Найдем расстояние между точками 
Найдем расстояние между точками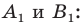 
Следовательно, мы показали, что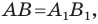 
то есть параллельный перенос сохраняет расстояние между точками. 
|
|
|
Следствие. Если фигура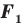 
— образ фигуры 
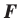при параллельном переносе, то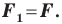 
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17. 5). 
Если фигура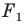 
является образом фигуры 
при параллельном переносе на вектор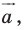 
то фигура 
является образом фигуры 
при параллельном переносе на вектор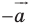 
(рис. 17. 6).
Параллельные переносы на векторы 
являются взаимно обратными движениями.
Пример №1
Каждой точке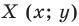 
фигуры 
ставится в соответствие точка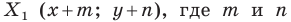 
— заданные числа. Докажите, что такое преобразование фигуры 
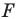является параллельным переносом на вектор 
Решение:
Рассмотрим вектор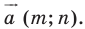 
Заметим, что координаты вектора 
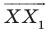равны 
то есть 
Следовательно, описанное преобразование фигуры 
— параллельный перенос на вектор 
Пример №2
Точка 
является образом точки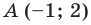 
при параллельном переносе на вектор 
Найдите координаты вектора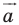 
и координаты образа точки 
Решение:
Из условия следует, что 
Отсюда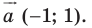 
Пусть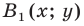 
— образ точки 
Тогда 
то есть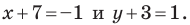 
Отсюда 
Ответ: 
Пример №3
Даны угол 
и прямая 
не параллельная ни одной из сторон этого угла (рис. 17. 7). Постройте прямую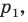 
параллельную прямой 
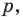так, чтобы стороны угла отсекали на ней отрезок заданной длины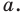 
Решение:
Рассмотрим вектор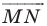 
такой, что 
и 
(рис. 17. 8). Построим луч 
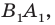являющийся образом луча 
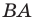при параллельном переносе на вектор 
Обозначим точку пересечения лучей 
буквой 
Пусть 
— прообраз точки 
при рассматриваемом параллельном переносе. Тогда 
Приведенные рассуждения подсказывают следующий алгоритм построения:
1. найти образ луча 
при параллельном переносе на вектор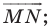 
2. отметить точку пересечения луча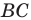 
с построенным образом;
3. через найденную точку провести прямую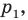 
параллельную прямой 
Прямая 
будет искомой.
|
|
|
