 |
Пример №12. Применение преобразований фигур при решении задач. Обозначим площади треугольников соответственно и Имеем:
|
|
|
|
Пример №12
Отрезок 
— высота прямоугольного треугольника 
Найдите радиус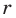 
вписанной окружности треугольника 
если радиусы окружностей, вписанных в треугольники 
соответственно равны 
Решение:
Поскольку угол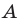 
— общий для прямоугольных треугольников 
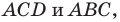то эти треугольники подобны (рис. 20. 13). Пусть коэффициент подобия равен 
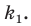Очевидно, что 
Аналогично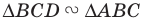 
с коэффициентом подобия 
Обозначим площади треугольников 
соответственно 
и 
Имеем:
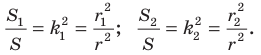
Отсюда 
Получаем, что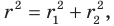 
Ответ: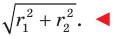 
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
На сторонах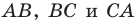 
остроугольного треугольника 
постройте такие точки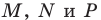 
соответственно, чтобы периметр треугольника 
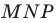был наименьшим.
Решение:
Пусть 
— произвольная точка стороны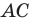 
треугольника 
точки 
— ее образы при симметрии относительно прямых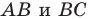 
соответственно (рис. 20. 34). Прямая 
пересекает стороны 
соответственно в точках 
Из решения задачи 2 п. 18 следует, что из периметров всех треугольников, для которых точка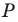 
фиксирована, а точки 
принадлежат сторонам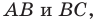 
периметр треугольника 
является наименьшим. Этот периметр равен длине отрезка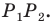 
Заметим, что отрезок 
— средняя линия треугольника 
Тогда 
Поскольку 
то точки 
лежат на одной окружности с диаметром 
Отсюда 
Следовательно, длина отрезка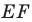 
будет наименьшей при наименьшей длине отрезка 
то есть тогда, когда 
— высота треугольника 
На рисунке 20. 35 отрезок 
— высота треугольника Алгоритм построения точек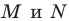 
понятен из рисунка.
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 
больше периметра треугольника 
Поэтому искомый треугольник является единственным — это построенный треугольник 
|
|
|
Можно показать (сделайте это самостоятельно), что точки 
и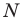 
являются основаниями высот, проведенных соответственно из вершин 
треугольника 
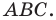
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 
Такой треугольник называют ортоцентрическим.
Пример №14
Точка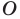 
— центр правильного 
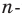угольника 
(рис. 20. 36). Докажите, что 
Решение:
Пусть 
Рассмотрим поворот с центром 
на угол 
например, против часовой стрелки. При таком преобразовании образом данного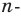 
-угольника будет этот же 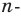угольник. Следовательно, искомая сумма не изменится. А это возможно лишь тогда, когда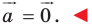 
Пример №15
Внутри треугольника 
все углы которого меньше 
найдите такую точку 
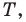чтобы сумма 
была наименьшей.
Решение:
Пусть 
— произвольная точка данного треугольника 
(рис. 20. 37). Рассмотрим поворот с центром 
на угол 
по часовой стрелке. Пусть точки 
— образы точек 
соответственно (рис. 20. 37). Поскольку поворот является движением, то 
Очевидно, что треугольник 
равносторонний. Тогда 
Имеем: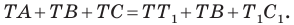 
Понятно, что сумма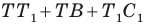 
будет наименьшей, если точки 
лежат на одной прямой. Поскольку 
то это условие будет выполнено тогда, когда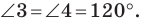 
Так как угол 
— образ угла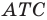 
при указанном повороте, то должно выполняться равенство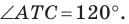 
Итак, точки 
будут принадлежать одной прямой тогда и только тогда, когда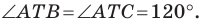 
Отсюда 
Таким образом, сумма 
будет наименьшей, если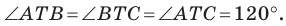 
Найти точку 
можно, например, построив ГМТ, из которых отрезки 
видны под углами 
(рис. 20. 38).
Понятно, что если один из углов треугольника 
не меньше 
то точка пересечения построенных дуг не будет расположена внутри треугольника. Можно показать, что в треугольнике с углом, не меньшим точка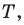 
сумма расстояний от которой до вершин треугольника является наименьшей, совпадает с вершиной тупого угла. 
|
|
|
|
|
|
