52.уравнение теплового пограничного слоя турбулентное движение среды

,                       (11)

известное под названием уравнения  Польгаузена.

Если учесть, что в соответствии с постулатом Фурье плотность теплового потока в рассматриваемом случае выражается как

,

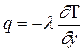то уравнение  (11)  можно представить в виде

                     (12)

Решая уравнения (11)  при известном заранее распределении скоростей в пограничном слое и при очевидных граничных условиях:

                             (13)

можно получить распределение температур в пограничном слое, а, следовательно, найти плотность теплового потока на поверхности.

52. уравнение теплового пограничного слоя турбулентное движение среды

При турбулентном режиме движения компоненты скорости и температуры являются сложными пульсирующими функциями времени, которые могут быть представлены в виде суммы осредненных по времени и пульсационных значений соответствующих величин.

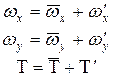
В левой части этих выражений - стоят мгновенные значения величин, в правой -осредненные во времени и пульсационные.

В дальнейшем будем считать, что все осредненные величины не меняются во времени. В этом случае осредненные значения пульсаций равны нулю .

Учитывая выше сказанное, после преобразований получим уравнение энергии для турбулентного пограничного слоя.

.          (14)

Сопоставляя уравнения  (12)  и  (14)  обнаруживаем появление в уравнении  (14)  новой величины . Эта величина имеет размерность плотности теплового потока и по физическому смыслу представляет собой количество тепла, переносимое через единицу поверхности в единицу времени в направлении перпендикулярном к потоку. Причем этот перенос осуществляется в результате турбулентного характера движения, т. е. вследствие поперечной пульсации скорости . 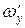Назовем эту величину плотностью турбулентного теплового потока

,                               (15)

а    - плотностью ламинарного теплового потока.

Следовательно, уравнение энергии для турбулентного пограничного слоя принимает вид

.               (16)

Появление в этом уравнении дополнительной неизвестной делает задачу неразрешимой. Для решения задачи необходимы дополнительные соотношения, которые можно получить с помощью полуэмпирической теории турбулентности Прандтля.

53. полуэмпиРическая теория турбулентности

прандтля для переноса тепла

Задача полуэмпирической теории применительно к процессам турбулентного переноса заключается в нахождении связи между плотностью турбулентного теплового потока q_T и осредненной температурой .

Предполагаем, что в турбулентном потоке имеется такое расстояние , называемое путем смешения для переноса тепла, на протяжении которого в среднем сохраняется постоянным теплосодержание турбулентного моля. Пройдя это расстояние, турбулентный моль скачком (пульсацией) изменит свое теплосодержание, смешиваясь с окружающей средой.

Пусть в плоскопараллельном турбулентном потоке, направленном вдоль оси  х  имеется некоторое распределение осредненной температуры по оси  у, .

В некоторой плоскости  1 - 1,  находящейся на расстоянии у  от плоскости отсчета, осредненная температура равна . Из этой плоскости выходит единичный моль среды, имеющий массу r  и теплосодержание 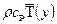   и движется за счет пульсации скорости в положительном направлении оси у.

В соответствии с нашим предположением этот моль будет сохранять постоянным свое осредненное теплосодержание    на протяжении пути смешения , а пройдя этот путь скачком изменит теплосодержание на величину соответствующую пульсации температуры, т. е. на величину . В результате моль будет иметь теплосодержание соответствующее осредненной температуре в плоскости 2 - 2  т. е. . Таким образом, получаем

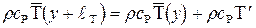
Разделив обе части этого выражения на постоянные величины плотности и теплоемкости, получим 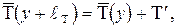  откуда

⇐ Предыдущая24252627282930313233Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: