44. Формула Ньютона-Рихмана. ТПОВ -температура поверхности тела, К;. 45.дифференциальные уравнения теплообмена. 46.дифференциальное уравнение конвективной

44. Формула Ньютона-Рихмана

Несмотря на то, что процесс конвективной теплоотдачи является весьма сложным и зависит от большого количества параметров, для описания этого процесса используется весьма простое выражение: формула Ньютона-Рихмана

q_ПОВ = a× ( T₀ - T_ПОВ ),

где   Т₀ - температура среды, К;

ТПОВ -температура поверхности тела, К;

a - коэффициент теплоотдачи,   Вт / (м²× К ).

Таким образом, коэффициент теплоотдачи есть плотность теплового потока, на границе среды и соприкасающегося тела, отнесенная к разности температур поверхности тела и окружающей среды. Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Коэффициент теплоотдачи есть величина, зависящая от режима движения и природы жидкости, явления теплопроводности, значений температур среды и поверхности, геометрических размеров и формы поверхности твердого тела, а также его расположения в потоке жидкости и скорости потока, омывающего поверхность тела.

45. дифференциальные уравнения теплообмена

Изучить какое-либо явление, значит, установить зависимость между величинами, характеризующими это явление. Для сложных явлений, в которых определяющие величины меняются и во времени и в пространстве, установить зависимость между переменными очень трудно. В таких случаях, применяя общие законы физики, ограничиваются установлением связи между переменными ( координатами, временем, физическими свойствами ), в области, охватывающей лишь небольшой промежуток времени и лишь элементарный объем из всего пространства. Полученная таким образом зависимость является общим дифференциальным уравнением рассматриваемого процесса.

После интегрирования этого уравнения получают аналитическую зависимость между величинами для всей области интегрирования и длявсего рассматриваемого интервала времени. Такие дифференциальные уравнения могутбыть составлены для любого процесса и, в частности, для процесса теплоотдачи.

Так как теплоотдача определяется не только тепловыми, но и гидродинамическими явлениями, то совокупность этих явлений описывается системой дифференциальных уравнений, в которую входят: уравнение теплоотдачи; уравнение энергии; уравнение движения; уравнение неразрывности ( сплошности ).

46. дифференциальное уравнение конвективной

теплоотдачи

Предположим, что вблизи поверхности некоторого тела произвольной формы движется жидкость ( газ ), имеющая характерную температуру  Т_Ж,   температура поверхности тела Т_ПОВ.

Известно, что скорость жидкости на поверхности тела равна нулю. Очевидно, что перенос тепла через этот бесконечно тонкий неподвижный слой жидкости может осуществляться лишь за счет молекулярной теплопроводности, т. е. этот перенос описывается постулатом Фурье

qПОВ = -l×                               (1)

где n - координата, направленная по нормали к поверхности тела;

n = 0 - соответствует точке на поверхности;

l - коэффициент теплопроводности жидкости,  Вт / (м× К).

С другой стороны, в соответствии с формулой Ньютона для конвективной теплоотдачи, плотность теплового потока на поверхности выражается как

q = a× ( ТЖ - ТПОВ ).                                (2)

Приравнивая на основании закона сохранения энергии правые части выражений (1)  и (2)  получим

a× ( ТЖ - ТПОВ ) = -l× .

Полученное уравнение называется дифференциальным уравнение теплоотдачи. Это уравнение позволяет получить формулу для коэффициента теплоотдачи

a =.

Коэффициент теплоотдачи можно найти, если известно распределение температур 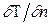  вблизи поверхности.

Температурный напор DT = T_Ж - Т_ПОВ  и коэффициент теплопроводности l  должны быть заданы.

Знаком пренебрегаем, так как коэффициент теплоотдачи принято считать величиной положительной.

 

47. дифференциальное уравнение энергии

( Уравнение теплопроводности для

ДВИЖУЩЕЙСЯ жидкости )

В дифференциальное уравнение конвективной теплоотдачи входит температурный градиент 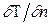.  Чтобы его найти, нужно вычислить поле температур.

Решение дифференциального уравнения энергии, которое в общем виде описывает процесс переноса тепла в движущейся однофазной среде, позволяет получить распределение температур в потоке жидкости.

У

Х

 

Имеем поток жидкости с некоторым произвольным распределением температуры  Т(x, y, z, t), и скорости 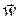  (x, y, z, t), считая, что жидкость несжимаема ( r = const ), скорость движения не слишком высока, что позволяет не учитывать выделение тепла вследствие вязкого трения, внутренние источники тепла отсутствуют, теплофизические свойства жидкости постоянны.

Рассмотрим элементарный объем  dV, представляющий собой прямоугольный параллелепипед с ребрами  dx, dy, dz - dV = dx× dy× dz  и связанный с неподвижной системой координат x, y, z.

Составим баланс тепла для этого элементарного объема, т. е. на основании закона сохранения энергии приравняем разность между поступившим и вышедшим из параллелепипеда количеством тепла к изменению энтальпии жидкости в объеме этого параллелепипеда.

В направлении оси х   в параллелепипед за время  dt  поступает следующее количество тепла

dQ_x = q_x× dy× dz× dt,

через противоположную грань выходит

dQ_x+dx = q_x+dx× dу× dz× dt,

где плотность теплового потока этой грани находят путем разложения в ряд Тейлора.

⇐ Предыдущая21222324252627282930Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: