 |
qx+dx = qx + dx. dQx - dQx+dx = - ×dV×dt. dQ3 = r×cP×dV× ×dt, (4). r×сР (5)
|
|
|
|
qx+dx = qx + dx.
Отсюда разность между количеством тепла поступившим в параллелепипед и вышедшим из него в направлении оси х.
dQx - dQx+dx = - × dV× dt.
Для осей y и z уравнения аналогичны.
qx qy qz - проекции вектора плотности теплового потока на оси координат.
Следовательно, общая разность между поступившим и вышедшим из параллелепипеда количеством тепла равна
d3Q = -, (3)
или dQ = -div 
× dV× dt.
С другой стороны, изменение теплосодержания жидкости в объеме dV за время dt составляет
dQ3 = r× cP× dV× × dt, (4)
где сР - удельная теплоемкость при постоянном давлении.
Приравнивая на основании закона сохранения энергии правые части (3) и (4) получим после сокращений
r× сР (5)
Процесс переноса тепла через объем параллелепипеда обусловлен во первых за счет молекулярной теплопроводности
(6)
и во вторых - конвективным переносом, обусловленным перемещением тепла с движущейся жидкостью
qКОН = r× сР× (7)
Таким образом, для каждой точки в потоке жидкости плотность теплового потока равна сумме этих двух величин, (6) (7).
q = r× cP× 
,
или для компонент вектора плотности теплового потока
qX = r× cP× , (8)
аналогично для qY и qZ.
Подставляя выражение (8) в уравнение (5) получим с учетом уравнения неразрывности
, (9)
где а = l / ср× r - коэффициент температуропроводности, м2 / с,
.
Полученное выражение (9) называется уравнением энергии, или уравнение переноса тепла в движущейся несжимаемой среде, или уравнение Фурье-Кирхгофа, или уравнение теплопроводности для движущейся жидкости.
|
|
|
Левая часть уравнения (9), представляет собой полную производную температуры по времени, и включает изменение температуры в данной точке во времени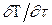 
- локальное изменение температуры; и изменение температуры, вызванное перемещением этой точки в поле переменной температуры вместе с движущейся жидкостью - конвективное изменение температуры 
. Эта величина называется субстанциональной производной температуры по времени.
Полученное уравнение позволяет при использовании соответствующих краевых условий и при известном распределении вектора скорости рассчитать распределение температуры в потоке жидкости и в частности вблизи поверхности твердого тела.
Следовательно, для определения распределения вектора скорости надо использовать уравнения, которые бы описывали изменение скорости во времени и пространстве. Такими уравнениями являются дифференциальные уравнения движения.
48. уравнение движения
Приведем уравнение движения без вывода в проекции только на ось х.
,
где gХ - проекция ускорения силы тяжести на ось х,
Р - давление жидкости,
n - коэффициент кинематической вязкости.
Аналогично можно написать проекции уравнения движения на оси у и z. Это уравнение Навье - Стокса.
Поскольку в уравнение движения входит неизвестная величина Р, то необходимо еще одно уравнение. Таким уравнением является уравнение неразрывности (сплошности).
49. уравнение неразрывности
Для несжимаемой жидкости ( r = const ) оно имеет вид
,
или, что то же самое div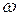 
= 0.
Тогда процесс конвективного теплообмена в однородной несжимаемой среде описывается следующей системой дифференциальных уравнений.
1). 
|
|
|
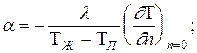
2). 
3). 
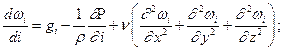
где i = x; y; z.
4). 
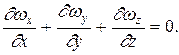
Эта система дифференциальных уравнений позволяет получить бесчисленное количество решений. Для того чтобы получить единственное решение, необходимо к системе дифференциальных уравнений присоединить условия однозначности, которые конкретизируют задачу и позволяют получить единственное решение.
Условия однозначности конвективного теплообмена состоят: из геометрических условий - характеризующих форму и размеры тела или системы, в которой протекает процесс; физических условий - характеризующих физические свойства среды; временных или начальных условий - характеризующих особенности процесса в начальный момент времени (для стационарных задач эти условия отпадают); граничных условий - характеризующих протекание процесса на границах жидкой среды.
|
|
|
