1. 4. 4. Выводы. 2. Формирование и анализ оптимального раскроя плитных материалов. 2. 1 Задача оптимального раскроя плитных материалов.

1. 4. 4. Выводы

Характер полученной расчетами кривой на графике соответствует теоретически ожидаемому. Полученное графоаналитическим методом значение постоянной времени Т = 54, 4 мин близко к значению постоянной времени Т = 54, 614 мин, рассчитанному аналитически. Некоторая величина расхождения между этими двумя значениями объясняется масштабом и погрешностями построения графика.

 

2. ФОРМИРОВАНИЕ И АНАЛИЗ ОПТИМАЛЬНОГО РАСКРОЯ ПЛИТНЫХ МАТЕРИАЛОВ.

2. 1 Задача оптимального раскроя плитных материалов.

Плиты одного из стандартных форматов подлежат раскрою на заготовки двух типоразмеров.

Допустим, возможно осуществить две схемы раскроя на двух имеющихся видах оборудования — станках 1 и 2. Для раскроя плиты на станке 1 по карте раскроя № 1 требуется 2 мин, по карте №2 — 4 мин, а на станке 2 по тем же картам раскроя требуется 3 мин и 9, 6 мин соответственно. Суммарное время работы станка 1 не должно превышать 240мин, а станка 2 — 480 мин.

По первому варианту раскроя можно получить 2 заготовки пер­вого типоразмера, 25 заготовок второго  и 4 заготовки третьего типоразмеров. Вторая схема раскроя позволяет разместить 10, 3 и 2 заготовки типоразмеров 1, 2 и 3 соответственно. По схеме раскроя № 1 —площадь отходов 4000 мм², по второй 2500 мм².  Требу­ется получить не менее 100 заготовок первого, не менее 250 заготовок второго и не менее 80 заготовок третьего типоразмера.

Решая задачу, следует выяснить, сколько плит надо раскроить по каждой из рассмотренных карт раскроя при выполнении планового за­дания на имеющемся оборудовании; при этом суммарное количество от­ходов должно быть минимальным.

Представим исходные данные в виде табл. 3. 1.

                                                                                                   Таблица 2. 1

Номер схемы раскроя	Отходы плиты, мм2	Норма времени раскроя на станке, мин		Количество заготовок,  шт., типоразмера
			9, 6
Фонд времени, мин				–	–	–
План выпуска заготовок, шт.

Обозначим через x₁ количество плит, раскраиваемых по первой схеме, через x₂ – по второй схеме раскроя.

Выражение для суммарного количества отходов имеет вид

 

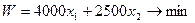                                                                                 (2. 1)

 

и представляет минимизированную целевую функцию задачи линейного программирования.

Выражения для ограничений по требуемому количеству заготовок:

 

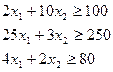                                                                                                       (2. 2)

 

Выражения для ограничений по длительности работы станков 1 и 2:

 

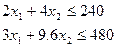                                                                                                      (2. 3)

Наконец, следует учесть естественные ограничения на неотрицательность переменных:

 

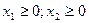                                                                                                             (2. 4)

 

Совокупность соотношений (2. 1)-(2. 4) представляет собой математическую модель данной задачи.

 

2. 2 Решение задачи линейного программирования

 

Графический метод является одним из способов решения задачи линейного программирования в том случае, когда модель содержит только две переменные. Для трех перемен­ных графическое решение задачи становится менее нагляд­ным, а при большем числе переменных — невозможным.

Построим область допустимых решений, в которой одновременно удовлетворяются все ограничения модели.

Область допустимых значений, определяемая ограничением, на тре­буемое количество заготовок первого типоразмера, находится заменой в ограничении знака неравенства на знак равенства:

 

                                                                                                   (2. 5)

 

и нахождением точек пересечения прямой (2. 5) с осями координат

при x₁=0 x₂=100/10=10,

при x₂=0 x₁=100/2=50.

 

Область, в которой выполняется ограничение в виде неравенства, указывается стрелкой, направленной в сторону допустимых значений пе­ременных. Аналогично строятся области допустимых значений перемен­ных и для других ограничений из (2. 2) и (2. 3).

Искомая область допустимых решений показана на рис. 2. 1, где ли­нии (/), (2), (3) отображают ограничения (2. 2), а линии (4), (5) — ограничения (2. 3).

 Рис. 2. 1 Построение области допустимых решений задачи оптимального

раскроя плитных материалов.

При построении области допустимых решений необходимо учитывать условия неотрицательности переменных (  и ), которые огра­ничивают область их допустимых значений первым квадрантом (часть плоскости, расположенной над осью x₁и правее оси x₂)

Таким образом, построена область ABCDEFA, внутри которой и на границах которой выполняются все ограничения.

Для нахождения оптимального решения в задачах минимизации вы­ясняется направление убывания, а в задачах максимизации — возраста­ния целевой функции.

Зададимся координатами двух произвольно выбранных, принадлежа­щих области допустимых решений точек .

Пусть  тогда значение целевой функции в точках A₁ и A₂

 

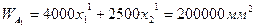                                                                               (2. 6)

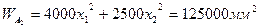                                                                          (2. 7)

 

Построив прямые 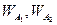 (см. рис. 2. 2), соответствующие выра­жениям (2. 6), (2. 7), определим направление убывания целевой функ­ции.

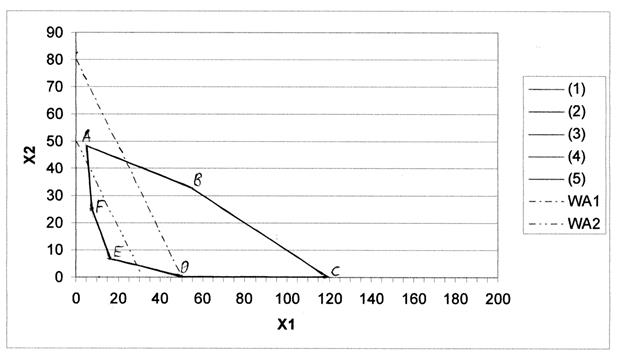Рис. 2. 2 Определение направления убывания целевой функции.

 

Чтобы найти оптимальное решение, следует перемещать прямую, ха­рактеризующую суммарные отходы, параллельно прямой W_A1 по на­правлению к началу координат, пока она не пересечется с точкой Е, которая и является оптимальной точкой. Даль­нейшее смещение прямой W_A1  в этом направлении будет приводить к по­паданию в область недопустимых решений.

Координаты оптимальной точки Е можно определить графически по рис. 2. 2 и аналитически как точки пересечения прямых (/) и (3), для чего необходимо решит систему уравнений:

 

                                                                                                     (2. 8)

 

Решив систему, получим . Тогда оптимальное значение целевой функции будет равно:

 

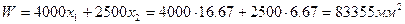
Вспомним, что через x₁ и х₂ мы обозначили интенсивность использо­вания схем раскроя первой и второй соответственно, т. е. переменные x₁ и x₂ по смыслу задачи должны быть целочисленными. Если условия целочисленности наложены на все переменные задачи, то она называется пол­ностью целочисленной. В рассмотренном выше примере была решена не­прерывная задача оптимального раскроя без учета целочисленности ре­шений. Поэтому для получения окончательного решения необходимо произвести округление координат полученного оптимума до допустимых целых значений так, чтобы полученное округленное решение принадле­жало области допустимых решений. В нашем примере получим 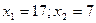. Для принятых значений x₁ , х₂ необходимо рассчитать значение целевой функции. Итак, окончательно имеем оптимальное значение с уче­том целочисленности решений

 

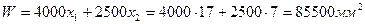
⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: