2.3. Анализ модели задачи линейного

2. 3. Анализ модели задачи линейного

 программирования на чувствительность

2. 3. 1. Задачи анализа модели на чувствительность

 

Анализом модели на чувствительность называется процесс исследования влияния возможных изменений параметров модели на оптимальное решение. В данной курсовой работе используем графический метод анализа модели на чувствительность на примере исследования модели, описанной ранее.

Отметим, что ограничения линейной модели могут быть активными и пассивными. Прямая, представляющая активное ограничение, должна проходить через оптимальную точку. В противном случае ограничение будет пассивным. Для нашего примера активными являются только те ограничения, которые определяют требуемое количество заготовок первого и третьего типоразмеров (прямые (1) и (3) на рис. 2. 1). Если некоторое ограничение является активным, то соответствующий ему ресурс называют дефицитным, ресурс же, связанный с пассивным ограничением называется недефицитным.

  Рассмотрим некоторые производственные ситуации, которые можно исследовать решая некоторые задачи анализа.

 

 

2. 3. 2. Ситуация 1

Допустим, что предприятие имеет возможность скорректировать план выпуска заготовок либо первого, либо второго типоразмеров. Необходимо выяснить: изменение плана выпуска заготовок какого типоразмера приведет к уменьшению суммарных отходов.

Поскольку заготовки первого типоразмера являются дефицитным ресурсом (см. рис. 2. 1 и пункт 2. 3. 1), то для уменьшения суммарных отходов необходимо корректировать план выпуска заготовок данного типоразмера, а изменение требуемого количества заготовок второго типоразмера (недефицитный ресурс) к изменению оптимального решения не приведет.

На рис. 2. 3 видно, что при уменьшении запаса первого ресурса (величины, зафиксированной в правой части ограничения (2. 2)) прямая (1) перемещается к началу координат параллельно самой себе, постепенно «стягивая» в точку Н треугольник EHD. Стороны ЕН и НD этого треугольника представляют собой продолжение прямых, соответствующих ограничениям (3) и оси x₁. Оптимальному решению при этом соответствует точка Н, а областью допустимых значений становится HFABCH. В точке Н ограничение для ресурса (1) становится избыточным, т. к. дальнейшее изменение запаса ресурса (1) не влияет ни на пространство решений, ни на оптимальное решение. Этот предельный уровень определяется нахождением координат точки Н, как точки пересечения прямых 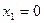 и (3), т. е. решением системы уравнений

 

                                                                                                               (2. 10)

 

Решив систему и подставив соответствующие решения ;  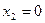в левую часть ограничения (2. 2) определим предельно допустимый запас ресурса (1)

 

 шт.

 

Таким образом, в данной ситуации целесообразно уменьшить план выпуска заготовок до 40 штук. Подставив координаты точки Н в выражение (2. 1) определим количество отходов в этой точке

 

 мм².

 

 

2. 3. 3. Ситуация 2

Предположим, что предприятие имеет возможность изменить план выпуска заготовок третьего типоразмера. Необходимо выяснить насколько целесообразно уменьшить план выпуска заготовок данного типоразмера, чтобы уменьшить суммарные отходы.

Аналогично ситуации 1 перемещаем прямую (3) до тех пор, пока треугольник EKF не «стянется» в точку К, которая и станет оптимальной точкой (см. рис. 2. 3). Координаты точки К найдем как координат точки пересечения ограничения (1) и (2), т. е. решением системы

 

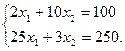                                                                                                             (2. 11)

 

Округлив и подставив полученные координаты ;  в левую часть ограничения (2. 4), получим предельно допустимое значение запаса ресурса (3)

 

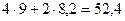 шт.

K

 

Суммарное количество отходов при этом составит

 

 мм².

 

 

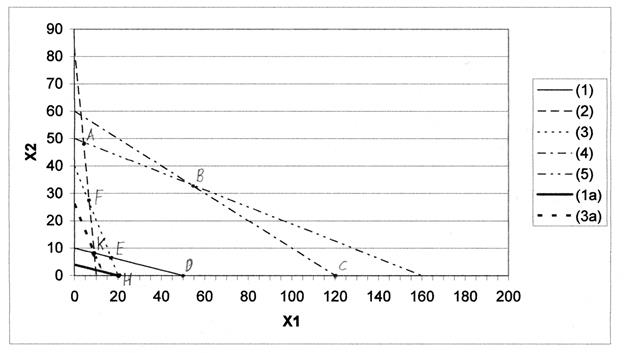Рис. 2. 3

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: