 |
2.4. Анализ модели на чувствительность
|
|
|
|
2. 4. Анализ модели на чувствительность
к изменениям коэффициентов целевой функции
Определим, каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения.
Также ответим на вопрос, насколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и наоборот, дефицитный ресурс сделать недефицитным.
Запишем выражение для целевой функции (см. формулу (2. 1))
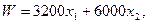 (2. 16)
(2. 16)
Обозначим коэффициент при  через
через 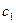 , а при
, а при 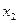 через
через  , тогда целевую функцию можно представить в виде
, тогда целевую функцию можно представить в виде
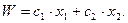 (2. 17)
(2. 17)
При увеличении  или уменьшении
или уменьшении 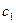 прямая, представляющая целевую функцию W, вращается против часовой стрелки (вокруг точки Е). Если же
прямая, представляющая целевую функцию W, вращается против часовой стрелки (вокруг точки Е). Если же  уменьшается или
уменьшается или 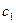 увеличивается, то эта прямая вращается по часовой стрелке. Таким образом, точка Е будет оставаться оптимальной, пока наклон прямой не выйдет за пределы, определенные наклонами прямых (1) и (3) (см. рис. 2. 5). Как только наклон прямой W выйдет за этот предел, получим некоторое новое оптимальное решение (точка F или точка D). Найдем допустимый интервал изменения
увеличивается, то эта прямая вращается по часовой стрелке. Таким образом, точка Е будет оставаться оптимальной, пока наклон прямой не выйдет за пределы, определенные наклонами прямых (1) и (3) (см. рис. 2. 5). Как только наклон прямой W выйдет за этот предел, получим некоторое новое оптимальное решение (точка F или точка D). Найдем допустимый интервал изменения 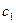 , при котором точка Е останется оптимальной. Исходное значение
, при котором точка Е останется оптимальной. Исходное значение 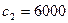 мм2 зафиксируем. На рис. 2. 5 видно, что значение
мм2 зафиксируем. На рис. 2. 5 видно, что значение 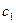 можно увеличивать до тех пор, пока прямая W не совпадет с прямой (1), или уменьшать, пока прямая W не совпадет с прямой (3). Для нахождения минимального и максимального значений коэффициента
можно увеличивать до тех пор, пока прямая W не совпадет с прямой (1), или уменьшать, пока прямая W не совпадет с прямой (3). Для нахождения минимального и максимального значений коэффициента 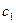 , при котором точка Е остается оптимальной, необходимо определить тангенсы углов наклона прямой W и прямых (1) и (3). Тангенс угла наклона a прямой вида
, при котором точка Е остается оптимальной, необходимо определить тангенсы углов наклона прямой W и прямых (1) и (3). Тангенс угла наклона a прямой вида  к оси
к оси  определяется по формуле
определяется по формуле
|
|
|
 , (2. 18)
, (2. 18)
тангенсы углов наклона прямых W; (1); (3) соответственно равны
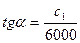 ,
,
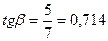 ,
,
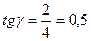 .
.
Максимальное значение 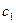 найдем из условия равенства наклонов прямой (1) и прямой W
найдем из условия равенства наклонов прямой (1) и прямой W
 , (2. 19)
, (2. 19)
 .
.
Минимальное значение 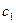 найдем из условия равенства наклонов прямой (3) и прямой W
найдем из условия равенства наклонов прямой (3) и прямой W
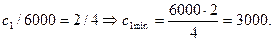
Аналогично рассчитаем максимальное и минимальное значение коэффициента  , фиксируя коэффициент
, фиксируя коэффициент 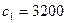
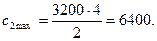
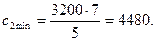
|
|
|

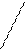
|
|

|
|
|
|

Рис. 2. 5
Представим решение этой задачи в виде табл. 2. 5. При этом статус ресурсов обозначен следующим образом, если в определенном интервале значений 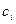 , что соответствует i-й строке табл. 2. 5, j-е ограничение задачи является активным, а связанный с ним ресурс дефицитным, то на пересечении i-й строки и j-го столбца табл. 2. 5 ставится 1, в противном случае (ограничение пассивное) ставится 0. Статус ресурса определяется так, например, при
, что соответствует i-й строке табл. 2. 5, j-е ограничение задачи является активным, а связанный с ним ресурс дефицитным, то на пересечении i-й строки и j-го столбца табл. 2. 5 ставится 1, в противном случае (ограничение пассивное) ставится 0. Статус ресурса определяется так, например, при  оптимум сменяется в точку F, при этом ограничение (3) становится пассивным, а соответствующий ему ресурс недефицитным. Ограничение (2) приобретает статус активного, а соответствующий ему ресурс становится дефицитным.
оптимум сменяется в точку F, при этом ограничение (3) становится пассивным, а соответствующий ему ресурс недефицитным. Ограничение (2) приобретает статус активного, а соответствующий ему ресурс становится дефицитным.
Таблица 2. 5
Результаты анализа статуса ресурсов
| Значение коэффициента | Статус j-го ресурса | Оптимальное решение | ||||
3000 < 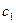 < 4285, 714 < 4285, 714
| точка Е | |||||
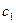 = 4285, 714 = 4285, 714
| линия EF | |||||
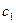 = 3000 = 3000
| линия DE | |||||
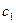 < 3000 < 3000
| точка D | |||||
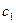 > 4285, 714 > 4285, 714
| точка F | |||||
4480 <  < 6400 < 6400
| точка Е | |||||
 = 6400 = 6400
| линия DE | |||||
 = 4480 = 4480
| линия EF | |||||
 < 4480 < 4480
| точка F | |||||
 > 6400 > 6400
| точка D | |||||
|
|
|
2. 5. Ситуация 6
Допустим, предприятие вынуждено перейти на использование плит большего формата по сравнению с существующим в настоящее время. Это приведет к тому, что площадь отходов по первой и второй схемам увеличится и составит 3300 мм2 и 6100 мм2 соответственно.
Необходимо осуществить прогноз минимального количества суммарных отходов и решить вопрос о допустимости применения старых карт раскроя при работе с новым форматом плит. Если минимальное количество суммарных отходов в новых условиях производства отличается от аналогичного показателя при старом формате плит более чем на 10%, то старые карты раскроя целесообразно сменить.
Выражение для целевой функции при изменении формата плит примет вид
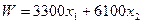 . (2. 21)
. (2. 21)
Определим, изменятся ли координаты оптимальной точки. Для этого найдем тангенс угла наклона целевой функции по формуле (2. 18)

Точка Е будет оставаться оптимальной до тех пор, пока выполняется условие
 (2. 22)
(2. 22)
Подставив в формулу (2. 22) полученные выше значения, получим

Следовательно, координаты оптимальной точки Е не изменяются. Подставив координаты этой точки в выражение для целевой функции, получим суммарное количество отходов при новом формате плит
 мм2.
мм2.
Найдем отличие от старого количества отходов
 .
.
Следовательно, смена существующих карт раскроя не является целесообразной.
|
|
|


