 |
3. Анализ и синтез структуры. Многостаночного участка. 3. 1. Задача исследования многоканальной системы с отказами. 3. 2. Построение графа
|
|
|
|
3. АНАЛИЗ И СИНТЕЗ СТРУКТУРЫ
МНОГОСТАНОЧНОГО УЧАСТКА
3. 1. Задача исследования многоканальной системы с отказами
Предположим, что имеется технологический участок цеха, включающий группу из 
лущильных станков.
Заявки на обслуживание (чураки) поступают с интервалом 
мин, время обработки заявки составляет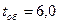 
мин. Предполагается, что заявки поступают в систему одним потоком и распределяются на обслуживании между свободными станками, т. е. обслуживается одновременно не более n заявок.
В курсовой работе требуется построить ориентированный размеченный граф состояний системы с заданными числовыми характеристиками процесса, построить математическую модель системы, рассчитать операционные характеристики системы и провести анализ ее функционирования, выработать рекомендации, направленные на повышение эффективности рассматриваемой системы.
3. 2. Построение графа
Для построения графа рассчитаем некоторые необходимые параметры, пользуясь исходными данными.
Интенсивность потока поступления заявок 
мин-1, определим по формуле
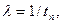(3. 1)
мин-1.
Интенсивность потока обслуживания заявок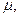 
мин-1, узнаем по формуле
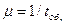(3. 2)
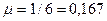мин-1.
Коэффициент использования системы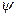 
вычислим по формуле
|
|
|
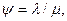(3. 3)
Вероятность простоя системы 
узнаем по формуле
, (3. 4)
Вероятность состояния системы, при котором в ней находится k заявок 
, определим по формуле
(3. 5)
где k = 
.
,
,
.
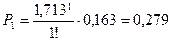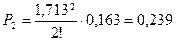Среднее число заявок, находящихся в системе (число работающих станков) Nc найдем по формуле
, (3. 6)
Среднее время пребывания заявок в системе определим по формуле
(3. 7)
мин.
Ориентированный граф состояний системы представлен на рис. 3. 1, где возможные состояния системы обозначены: S0 – система свободна (все станки не заняты); S1 – один станок занят; S2 – два станка заняты; S3 – все три станка заняты (система отказывает в обслуживании).
мин-1
|
|
|
| ||||||||||||||
 |  |  | |||||||||||||||
мин-1 
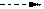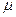
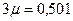мин-1 
мин-1
|
|
|
 |
Рис. 3. 1. Ориентированный граф состояний системы
3. 3. Построение математической модели
Математическая модель системы будет описана формулами (3. 4); (3. 5); (3. 6), для построения графиков зависимости 
и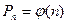 
выполним расчеты зависимости для 
и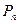 
при n = 1; 2; 3; 4; 5; 6; 7; 8 и представим их виде табл. 3. 1, пример расчетов см. в пункте 3. 2. Графики и 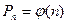представлены на рис. 3. 2 и рис. 3. 3, соответственно.
Таблица 3. 1
Зависимость Nc и Рn от n
| 
|
|
|
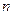
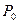
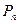
| 0, 714 | 1, 2245 | 2, 400 | |
| 0, 077 | 0, 1130 | 6, 462 | |
| 0, 163 | 0, 1367 | 2, 140 | |
| 0, 122 | 0, 0440 | 1, 772 | |
| 0, 105 | 0, 0129 | 1, 725 | |
| 0, 099 | 0, 0035 | 1, 716 | |
| 0, 097 | 0, 0008 | 1, 715 | |
| 0, 096 | 0, 0002 | 1, 714 |
Рис. 3. 2. График зависимости
Рис. 3. 3. График зависимости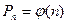
3. 4. Анализ функционирования системы
Зная операционные характеристики многоканальной системы (рассчитанные в пунктах 3. 2 и 3. 3), можно определить ее структуру. Стоимостный критерий оптимизации в данном случае ориентирован на определение оптимального числа станков (каналов обслуживания) при минимизации затрат
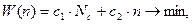(3. 8)
где 
– отнесенные к единице времени затраты на обеспечение работы дополнительного
станка;
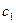– показатель затрат, обусловленный ожиданием детали.
Вычислительная процедура минимизации W(n) эквивалентна выполнению условий неравенства
(3. 9)
Подставив в неравенство (3. 9) величину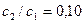 
из задания и данные из табл. 3. 1, можно убедиться, что неравенство выполняется при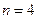 
1, 772-1, 725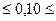 
2, 14-1, 772
0, 047 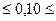0, 368
3. 5. Выводы
На основании данных, полученных в пунктах 3. 2; 3. 3; 3. 4 можно утверждать, что при данных условиях ( 
= 3, 5 мин;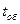 
= 6, 0 мин) оптимальное число каналов обслуживания 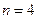, следовательно, число станков можно изменить
Из анализа графиков на рис. 3. 2 и рис. 3. 3 можно заключить, что увеличение числа станков свыше пяти не приведет к существенному изменению параметров системы.
|
|
|
|
|
|
