 |
Через любые 2 точки можно провести прямую и притом только одну.
|
|
|
|
Билет. 1
1. (п. 1) К основным геометрическим фигурам на плоскости относятся точка и прямая линия.
Точка —это самая малаягеометрическая фигура, которая является основой всех прочих построений(фигур).
Прямую линию, или прямую, можно представить себе как бесчисленное множествоточек, которыерасположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
 |
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком.
Отрезок изображается так: 
Длина отрезка -положительное число, показывающее, сколько раз единичный отрезок и его части
укладываются в данном отрезке. Длину отрезка АВ также называют расстоянием между точками А и В. Свойства:
1) Длины равных отрезков равны;
2) Длина суммы отрезков равны сумме их длин.
Обычно прямые обозначаются малыми латинскими буквами a, b, c, d, а точки – большими A, B, C...
Через любые 2 точки можно провести прямую и притом только одну.
Любые 2 прямые на плоскости либо имеют одну общую точку (пересекаются), либо не имеют общих точек (параллельны).
2. (п. 20) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Дано: ∆ АВС и∆ А1В1С1, у них АВ=А1В1, АС=А1С1, ВС=В1С1. Доказать, что∆ АВС= ∆ А1В1С1
Доказательство: Приложим∆ АВС к∆ А1В1С1так, чтобы сторона АВ совпала со стороной А1В1, а точки С и С1 оказались по разные стороны от АВ.
По условию АС=А1С1, ВС=В1С1 → ∆ А1С1С и ∆ В1С1С – равнобедренные, а значит ∠ 1 = ∠ 2, ∠ 3 = ∠ 4 (углы при основании), поэтому весь ∠ А1СВ1 = ∠ А1С1В1.
|
|
|
Итак, мы получили, что АС=А1С1, ВС=В1С1, ∠ С = ∠ С1, следовательно ∆ АВС = ∆ А1В1С1
(по I признаку). Ч. т. д. 3. Найдите величины смежных углов, если один в5раз больше другого.
Решение: Обозначим один из угловх, другой значит будет5х, т. к. он в5раз больше.
Сумма смежных углов всегда 1800, получаем уравнение х + 5х = 1800, откуда 6х = 1800, х = 300. Значит один из смежных углов 300, другой 30*5 = 1500.
Билет. 2
1. (п. 14) Треугольник –это геометрическая фигура, состоящая из трех точек, не лежащих на однойпрямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его
сторонами. Виды треугольников:
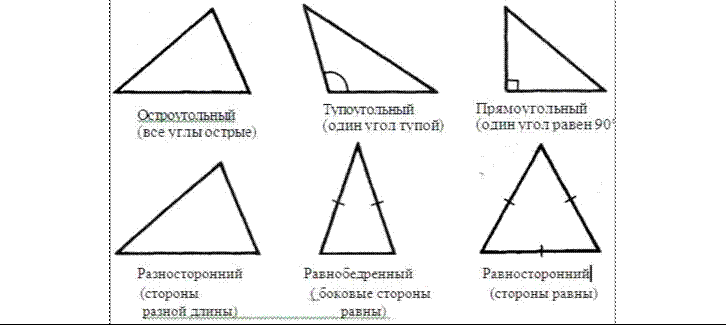
2. (п. 25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
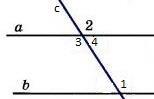Дано: прямые а и b, с –секущая, соответственные углы∠ 1 =∠ 2.
Доказать, что а||b
Доказательство: ∠ 1 =∠ 2 (по условию), ∠ 2 =∠ 3 (вертикальные), следовательно ∠ 1 = ∠ 3, а это накрест лежащие углы, поэтому а||b.
Ч. т. д.
3. Отрезки АС и ВМ пересекаются в точке О и делятся ею пополам. Докажите, что∆ АВС= ∆ СМА.
 |
Дано: АО=ОС и ВО=ОМ. Доказать, что∆ АВС= ∆ СМА
Доказательство: Пусть отрезки АС и ВМ пересекаются в точке О. Тогда ∆ АОВ = ∆ СОМ по I признаку (АО = ОС и ВО = ОМ по условию, а ∠ АОВ = ∠ СОМ как вертикальные). Следовательно, ∠ ВАО = ∠ МСО и сторона АВ = МС (в равных треугольниках против равных углов лежат равные стороны).
Тогда ∆ АВС = ∆ СМА тоже по I признаку (∠ ВАО = ∠ МСО, АВ = МС, АС – общая сторона). Ч. т. д.
Билет. 3
1. (п. 17)
Медиана –это отрезок, идущий из вершинытреугольника к середине противоположной стороны. (Нельзя говорить идущий в противоположную сторону…)
|
|
|
А1
А
Биссектриса –это отрезок, идущий из вершинытреугольника к противоположной стороне и
делящий угол треугольника пополам.
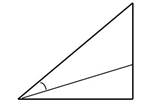
А1
300
А 
300
 |
Высота –это перпендикуляр, идущий из вершинытреугольника к противоположной стороне.
( Перпендикуляр – это отрезок, падающий под углом в 900 к прямой).
Высота – это единственная линия в треугольнике, которая при построении может оказаться снаружи треугольника.
В любом треугольнике все 3 медианы пересекаются в одной точке, все 3 биссектрисы пересекаются в одной точке и все 3 высоты пересекаются в одной точке.
|
|
|
