 |
2. (п.29) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
|
|
|
|
2. (п. 29) Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Дано: а||b, с –секущая,
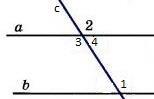Доказать, что соответственные углы∠ 1 =∠ 2.
Доказательство: т. к. а||b, то∠ 1 =∠ 3 (накрест лежащие), а∠ 3 =∠ 2(вертикальные), следовательно ∠ 1 = ∠ 2. Ч. т. д.
3. Найти смежные углы, если один из них на450больше другого.
| Решение: Обозначим ∠ 2 =х, тогда∠ 1 =х+ 450. | |
| ∠ 1 | По свойству смежных углов ∠ 1 + ∠ 2 = 1800. |
| ∠ 2 | Составим уравнение х + х + 450 = 1800; 2х = 1350; х = 1350: 2 = 67, 50. |
| Значит ∠ 2 = 67, 50, тогда ∠ 1 = 67, 50 + 450 = 112, 50. |
Ответ: ∠ 1 = 112, 50; ∠ 2 = 67, 50.
Билет. 12
 1. (п. 11) Смежные углы–это два угла, у которых одна сторона общая,
| ∠ 1 | |
| а две другие являются продолжениями одна другой. | ∠ 2 | |
Свойство: Сумма смежных углов равна 1800.
На рисунке ∠ 1 и ∠ 2 вместе образуют развернутый угол, а он равен 1800, следовательно, ∠ 1 + ∠ 2 = 1800.
2. (п. 35) Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Дано: ∆ АВС и∆ А1В1С1–прямоугольные, АВ=А1В1и СВ=С1В1, углы С и С1 – прямые.
Доказать, что∆ АВС= ∆ А1В1С1 Доказательство: т. к. ∠ С=∠ С1= 900, то∆ АВС можно наложить на
∆ А1В1С1 так, что вершина С совместится с С1, а стороны СА и СВ наложатся на лучи С1А1 и С1В1. По условию СВ = С1В1, значит, вершина В совместится с В1. Но тогда и вершина А совместится с А1.
Ч. т. д.
3. Докажите, что если биссектриса треугольника совпадает с его высотой, то треугольник равнобедренный.
Дано: В∆ АВС биссектриса ВД–это высота. Доказать, что∆ АВС равнобедренный. Доказательство: ∆ АВД= ∆ СВД по второму признаку
|
|
|
(∠ 1 =∠ 2, т. к. ВД – биссек., ∠ 3 =∠ 4=900, т. к. ВД – высота, а сторона ВД – общая).
Значит АВ = ВС, т. е. Δ ABC – равнобедренный. Ч. т. д.
Билет. 13
| 1. (п. 11) Вертикальные углы – это два угла, у которых | стороны одного угла | являются | |
| продолжениями сторон другого. | |||
| Теорема: Вертикальные углы равны. | |||
| Доказательство: ∠ 1 +∠ 2 = 1800(смежные), | |||
| ∠ 3 + ∠ 2 = 1800 (смежные), | → ∠ 1 = ∠ 3. Ч. т. д. | ||
2. (п. 35) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Дано: ∆ АВС и∆ А1В1С1–прямоугольные, АВ=А1В1, ∠ С=∠ С1= 900, ∠ В=∠ В1. Доказать, что∆ АВС= ∆ А1В1С1
Доказательство: т. к. ∠ С=∠ С1= 900и∠ В=∠ В1, следовательно, ∠ А=∠ А1(по теореме о сумме углов втреугольнике), а значит ∆ АВС равен ∆ А1В1С1 по второму признаку равенства треугольников (у них равны гипотенуза и два прилежащих к ней угла). Ч. т. д.
3. Отрезки АВ и СЕ пересекаются в их общей середине О. На отрезках АС и ВЕ отмечены точки К и М так, что АК = ВМ. Доказать, что ОК = ОМ.
Доказательство: Соединим точки А, С, В, Е. Получиличетырёхугольник, диагонали которого делятся точкой пересечения пополам. А, значит, этот четырёхугольник – параллелограмм. ЕС и АВ – диагонали параллелограмма АСВЕ. ∠ ОАС = ∠ ОВЕ (как накрест лежащие при параллельных прямых АС и ВЕ и секущей АВ). Получили, что ∆ АОК = ∆ ВОМ по первому признаку равенства треугольников (АО = ОВ, АК = МВ, ∠ ОАС = ∠ ОВЕ). В равных треугольниках оставшиеся стороны равны, т. е. ОК = ОМ. Ч. т. д.
Билет. 14
1. Отложить на данном луче от его начала отрезок, равный данному. Смотри презентацию, слайд 2.
|
|
|
2. (п. 18) В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Дано: ∆ АВС, АВ=ВС, ВО–биссектриса. Доказать, что ВО–медиана и высота.
Доказательство: Рассмотрим ∆ ABO и ∆ CBO. У них:
AB = BC (по условию), BO – общая сторона, ∠ AВO = ∠ СВО (т. к. BO – биссектриса). Значит эти треугольники равны по 1 признаку. Следовательно, AO = OС, а значит BO – медиана.
Далее, ∠ AOC – развернутый угол = 180°. Но т. к. ∆ ABO = ∆ CBO, то ∠ AOB = ∠ COB = 180°/2 = 900, значит BO – высота. Ч. т. д.
3. Один из углов прямоугольного треугольника равен600, а сумма гипотенузы и меньшего из катетов равна26, 4см. Найдите гипотенузу треугольника.
Решение: Пусть в данном треугольнике∠ В= 900, ∠ A = 600.
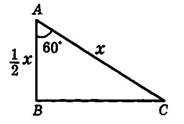
Тогда ∠ С = 1800 – 900 – 600 = 300. Меньший из катетов лежит напротив угла в 300 и, значит, равен половине гипотенузы (по 2 свойству). Обозначим
гипотенузу АС = х, тогда катет АВ = ½ *х. Составляем уравнение: х + 12 х = 26, 4 (по условию). Отсюда 32 х = 26, 4 или х = 17, 6. Ответ: гипотенуза АС= 17, 6см.
 | |
|
|
|
