 |
1. (п.29)Во всякой теореме есть2части:условиеизаключение.Условие теоремы–это то,что дано,азаключение – то, что требуется доказать.
|
|
|
|
Билет. 15
1. (п. 29)Во всякой теореме есть2части: условиеизаключение. Условие теоремы–это то, что дано, азаключение – то, что требуется доказать.
Например, рассмотрим теорему: Если 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника, то такие треугольники равны. В ней условием будет утверждение: 3 стороны первого треугольника соответственно равны 3 сторонам второго треугольника (это дано), а
заключение: треугольники равны(это требуется доказать).
Теоремой, обратной данной, называется такая теорема, в которой условие и заключение меняютсяместами.
Например, для данной выше теоремы обратной теоремой будет: Если треугольники равны, то у них все стороны соответственно равны.
Или для теоремы: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Обратная теорема будет звучать так: Если две параллельные прямые пересечены секущей, то соответственные углы равны.
2. (п. 28) Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство: Действительно, пусть а ||с и b ||с. Докажем, что тогда а || b.
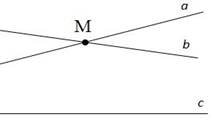
Допустим, что прямые а и b не параллельны, т. е. пересекаются в какой-то точке М. Тогда получим, что через точку М проходят 2 прямые (а и b) параллельные прямой с, а это противоречит аксиоме параллельных прямых. Поэтому наше предположение было неверным, а значит, прямые а и b параллельны.
3. Разность двух односторонних углов при пересечении двух параллельных прямыхсекущей равна 500. Найти эти углы.
Решение: Т. к. а||b, ∠ 1 +∠ 2 = 1800. Пусть∠ 1 =х, тогда∠ 2 =х–50.
Составляем уравнение: х + х – 50 = 180. 2х = 230, х = 115,
т. е. ∠ 1 = 1150, ∠ 2 = 550.
|
|
|
Билет. 16
1. Как построить треугольник по стороне и двум прилежащим к ней углам. Смотри презентацию,
слайд 9.
2. (п. 30) Внешним углом треугольника называется угол, смежный с каким-нибудь углом этоготреугольника.
Свойство: Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Дано: ∆ АВС, ∠ 4–внешний.
Доказать, что∠ 4 =∠ 1 +∠ 3.
Доказательство: ∠ 1 + ∠ 3 + ∠ 2 = 1800 (по теореме о сумме углов ∆ ).
∠ 4 + ∠ 2 = 1800 (смежные)
Следовательно, ∠ 4 = ∠ 1 + ∠ 3. Ч. т. д.
3. Через середину отрезка проведена прямая. Доказать, что концы отрезка равноудалены от этой прямой. Дано: О–середина АВ, l –прямая, проходящая через О.
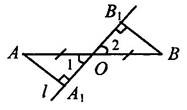Доказать, что АА1=ВВ1.
Доказательство: АА1^ l иВВ1^ l. Рассмотрим прямоугольныетреугольники АОА1 и ВОВ1. Они равны по гипотенузе и острому углу (АО = ОВ по условию, ∠ 1 =∠ 2, как вертикальные).
Следовательно, АА1 = ВВ1. Ч. т. д.
Билет. 17
1. (п. 24, 37) Две прямые называются параллельными, если они лежат в одной плоскости и непересекаются. Обозначение: а ǀ ǀ b.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки кпрямой.
Расстоянием между параллельными прямыми называется расстояние от произвольной точки одной изпараллельных прямых до другой прямой.
2. (п. 32) В треугольнике против большего угла лежит большая сторона.
Дано: ∆ АВС, ∠ С> ∠ В.
Доказать, что АВ> АС.
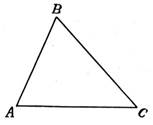
Доказательство: Предположим, что это не так.
Тогда либо АВ = АС, либо АВ < АС. В первом случае получаем, что ∆ АВС
– равнобедренный, а значит углы при основании равны, т. е. ∠ С=∠ В, а это противоречит условию, что ∠ С > ∠ В. Во втором случае получаем, что ∠ С < ∠ В (т. к. против большей стороны лежит больший угол). Это тоже противоречит условию. Значит, наше предположение неверно, и, следовательно, АВ > АС. Ч. т. д.
|
|
|
3. В∆ АВС∠ А= 400, а∠ ВСЕ смежный с∠ АСВ равен800. Доказать, что биссектриса∠ ВСЕпараллельна прямой АВ.
Дано: ∠ А= 400, а∠ ВСЕ= 800, СК–биссектриса∠ ВСЕ.
Доказать, СКǀ ǀ АВ.
Доказательство: ∠ ВСК=∠ КСЕ=½ ∠ ВСЕ= 800/2 = 400.
Получили, что ∠ ВАС = ∠ КСЕ = 400, а это соответственные углы при прямых АВ, СК и секущей АС. Раз они равны, то СК ǀ ǀ АВ. Ч. т. д.
|
|
|
