 |
2. (п.25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
|
|
|
|
Билет. 24
1. (п. 14) Треугольник–это геометрическая фигура, состоящая из трех точек, не лежащих на однойпрямой, соединенных отрезками. Точки называются вершинами треугольника, а отрезки – его
сторонами. Виды треугольников:
 |
2. (п. 25) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
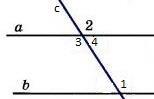Дано: прямые а и b, с –секущая, соответственные углы∠ 1 =∠ 2.
Доказать, что а||b
Доказательство: ∠ 1 =∠ 2 (по условию), ∠ 2 =∠ 3 (вертикальные), следовательно ∠ 1 = ∠ 3, а это накрест лежащие углы, поэтому а||b.
Ч. т. д.
3. В равнобедренном треугольнике одна сторона равна25см, а другая10см. Какая из них являетсяоснованием?
Решение: В треугольнике каждая сторона должна быть меньше суммы двух других. Тогда, если основаниеравно 10 см, то каждая сторона удовлетворяет такому условию. Но если основание равно 25 см, то 25 см > 10 см + 10 см - это не верно. Значит, есть только одно правильное решение.
Ответ: основание равно10см.
Билет. 25
 |
1. (п. 31) Прямоугольный треугольник–это треугольник, у которого один уголпрямой, т. е. равен 900.
Сторона, лежащая напротив прямого угла, называется гипотенузой, а две другие стороны - катетами. Гипотенуза всегда большего любого из катетов, т. к. лежит напротив большего угла в треугольнике.
2. (п. 30) Сумма углов в треугольнике 1800.
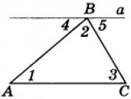Дано: ∆ АВС.
Доказать, что∠ А+∠ В+∠ С= 1800.
Доказательство: Проведем через вершину В прямую а, параллельную стороне АСОчевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.
|
|
|
∠ 4 + ∠ 2 + ∠ 5 = 180° (*).
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей
| АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей | ||
| ВС. Поэтому ∠ 4 = ∠ 1 = ∠ А, ∠ 5 = ∠ 3 = ∠ С. Отсюда, учитывая равенство (*), получаем: | ||
| ∠ l + ∠ 2 + ∠ 3 = 180°, или ∠ A + ∠ B + ∠ C = 180°. Ч. т. д. | Д | |
| А | ||
| 3. Прямые АВ и СД пересекаются в точке О, ∠ AОС= 580. Найдите∠ ВОД. | О | |
| Решение: ∠ ВОД=∠ AОС= 580, т. к. они вертикальные. | 580 | |
| С | В | |
|
|
|
