 |
2. (п.25) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
|
|
|
|
2. (п. 25) Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Дано: прямые а и b, АВ –секущая, накрест лежащие углы∠ 1 =∠ 2.
Доказать, что а||b
Доказательство: (метод от противного). Предположим, что прямые а и b не параллельны, а значит они пересекаются в некоторой точке М. Рассмотрим ∆ АВМ: ∠ 1 будет внешним углом для этого треугольника, а ∠ 2 – внутренним. Из теоремы о внешнем угле треугольника следует, что ∠ 1 больше ∠ 2, а это противоречит условию (∠ 1 = ∠ 2), значит, прямые а и b не могут пересекаться, поэтому они параллельны. Ч. т. д.
3. На окружности с центром О отмечены точки А и В так, что ∠ АОВ – прямой. Отрезок ВС – диаметр окружности. Докажите, что хорды АВ и АС равны.
 | ||
 | ||
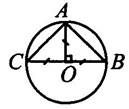Доказательство: Рассмотрим∆ ВОА и∆ СОА, у них сторона ОА–общая, СО=ОВ(как радиусы одной окружности), ∠ СОА = ∠ ВОА = 900.
Следовательно, ∆ ВОА = ∆ СОА по I признаку. А раз треугольники равны, то их соответственные стороны тоже равны, т. е. АВ = АС. Ч. т. д.
Билет. 4
1. (п. 37) Пусть ВА-перпендикуляр, опущенный из точки В на прямуюа, и С–любая точка на прямой а, отличная от точки А (основание перпендикуляра). Отрезок ВС называется наклонной, проведенной из точки В к прямой а. Точка С называется основанием наклонной, а отрезок АС — проекцией наклонной.
Расстоянием от точки В до прямой а называется длина перпендикуляра из этойточки к данной прямой, т. е. длина отрезка ВА.
Перпендикуляр, проведённый из какой-нибудь точки к прямой, меньше всякой наклонной, проведённой из той же точки к этой прямой. Поэтому расстояние от точки В до прямой а является наименьшим из расстояний от точки В до любой из точек прямой а.
|
|
|
2. (п. 25) Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
Дано: прямые а и b, с –секущая, односторонние углы∠ 1 +∠ 4 = 1800.
Доказать, что а||b
Доказательство: ∠ 1 +∠ 4 = 1800(по условию), ∠ 3 +∠ 4 = 1800(смежные), следовательно ∠ 1 = ∠ 3, а это накрест лежащие углы, поэтому а||b. Ч. т. д.
3. Два внешних угла треугольника равны(∠ 1 =∠ 2). Периметр равен74см, а одна из сторон АС= 16см. Найдите две другие стороны треугольника.
Решение: По условию∠ 1 =∠ 2, следовательно∠ А=∠ С(как смежные с равными углами), а значит∆ АВС – равнобедренный, т. е. АВ = ВС = х. Периметр – это сумма всех сторон, составим уравнение:
х + х + 16 = 74см
2х = 74 – 16
2х = 58
х = 29см = АВ = ВС. Рассмотрим другой случай:
Билет. 5
1. (п. 24) Две прямые называются параллельными, если они лежат в однойплоскости и не пересекаются. Обозначение: m || n.
Все точки одной параллельной прямой находятся на одинаковом расстоянии от другой параллельной прямой.
Все прямые, параллельные одной прямой, параллельны между собой. Принято считать, что угол между параллельными прямыми равен нулю. Все перпендикуляры к одной и той же прямой параллельны между собой.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
2. (п. 15) Если 2 стороны и угол между ними одного треугольника соответственно равны 2 сторонам и углу между ними другого треугольника, то такие треугольники равны.
Дано: ∆ АВС и∆ А1В1С1, у них АВ=А1В1, АС=А1С1, ∠ А=∠ А1. Доказать, что∆ АВС= ∆ А1В1С1
Доказательство: Наложим∆ АВС на∆ А1В1С1так, чтобывершина А совпала с вершиной А1. Так как по условию ∠ А = ∠ А1, то луч АВ наложится на луч А1В1, а луч АС на луч А1С1. Еще по условию АВ=А1В1, значит точка В совпадет с точкой В1, АС=А1С1, значит точка С совпадет с точкой С1. Все три точки у треугольников совпали, значит они равны. Ч. т. д.
|
|
|
3. В равнобедренном∆ АВС с основанием ВС проведена медиана АМ. Найдите её длину, еслипериметр ∆ АВС = 32см, а периметр ∆ АВМ равен 24см.
Решение: РАВС=АВ+ВС+АС
32 = 2АВ+2ВМ (т. к. АВ=АС и ВМ=МС) 32 = 2(АВ + ВМ)
16 = АВ + ВМ.
РАВМ = АВ+ВМ+АМ, 24 = 16 + АМ, следовательно АМ = 24 – 16 = 8см.
Ответ: АМ= 8см.
 |
|
|
|
