 |
1.Как построить биссектрису данного угла. Смотри презентацию, слайд 4.
|
|
|
|
Билет. 18
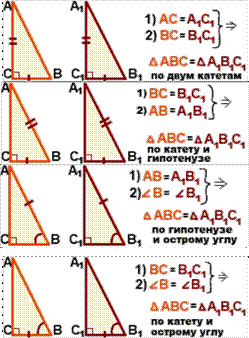
1. (п. 35) Признаки равенства прямоугольных треугольников:
1) по двум катетам: Если два катета одногопрямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
2) по катету и гипотенузе: Если катет и гипотенуза одногопрямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
3) по гипотенузе и острому углу: Если гипотенуза иострый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
4) по катету и острому углу: Если катет и острый уголодного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
2. (п. 11) Вертикальные углы –это два угла, у которых стороны одного угла являютсяпродолжениями сторон другого.
| Теорема: Вертикальные углы равны. | ||
| Доказательство: ∠ 1 +∠ 2 = 1800(смежные), | ||
| ∠ 3 + ∠ 2 = 1800 (смежные), | → ∠ 1 = ∠ 3. Ч. т. д. |
3. В равнобедренном∆ АВС с основанием АС= 37см, внешний угол при вершине В равен600. Найтирасстояние от вершины С до прямой АВ.
Дано: ∆ АВС–равнобед., внешний∠ НВС= 600, АС=37см, СН^АВ(т. к. это расстояние).
Найти: длину СН.
Решение: По свойству внешнего угла∠ НВС=∠ А+∠ С= 600. А т. к. ∆ АВС – равнобед., то ∠ А = ∠ С = 600/2 = 300 (углы при основании). В прямоугольном треугольнике АНС, ∠ А = 300, значит катет лежащий
напротив него равен половине гипотенузы, т. е. СН = 12 АС = 37: 2 =18, 5см. Ответ: СН = 18, 5см.
|
|
|
 | |||
 | |||
Билет. 19
1. Как построить треугольник по трем сторонам. Смотри презентацию, слайд 8. Задача имеет решение только когда выполняется неравенство треугольника, т. е. сумма двух любых сторон должна быть больше третьей стороны.
2. (п. 32) В треугольнике против большей стороны лежит больший угол.
Дано: ∆ АВС, АВ> АС.
Доказать, что∠ С> ∠ В
Доказательство: Отложим на стороне АВ отрезокAD=АС. Так какAD < АВ, тоточка D лежит между точками А и В. Следовательно, ∠ 1 является частью ∠ С и, значит, ∠ C > ∠ 1. Угол 2 – внешний угол ∆ BDC, поэтому ∠ 2 > ∠ В. ∠ 1 = ∠ 2 как углы
при основании равнобедренного треугольника ADC. Таким образом, ∠ С > ∠ 1, ∠ 1 = ∠ 2, ∠ 2 > ∠ B. Отсюда следует, что ∠ С > ∠ В. Ч. т. д.
3. Основание равнобедренного треугольника равно8см. Медиана, проведенная к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного треугольника на 2см больше периметра другого. Найти боковую сторону данного треугольника.
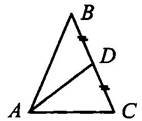
Решение:
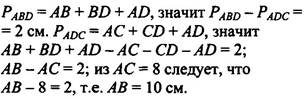
Билет. 20
1. Как построить биссектрису данного угла. Смотри презентацию, слайд 4.
2. (п. 18) В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
Дано: ∆ АВС, АВ=ВС, ВО^АС(высота). Доказать, что ВО–медиана и биссектриса.
Доказательство: Рассмотрим ∆ ABO и ∆ CBO. У них:
AB = BC (по условию), ∠ A = ∠ С = х (углы при основании в равноб. ∆ ), ∠ AВО = ∠ СВО = 900 – х (по теореме о сумме углов в ∆ ).
Значит эти треугольники равны по 2 признаку. Следовательно, AO = OС, а значит BO – медиана.
Далее, ∠ AВО = ∠ СВО = 900 – х, значит BO – биссектриса. Ч. т. д.
3. В прямоугольном треугольнике АВС с прямым углом С внешний угол при вершине А равен1200, АС + АВ = 18см. Найти АС и АВ.
|
|
|
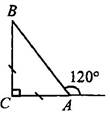
Решение: В∆ АВС: ∠ А= 1800–1200= 600(смежные).
∠ В = 1800 – 900 – 600 = 300 (по теореме о сумме углов в ∆ ). Следовательно, катет лежащий напротив ∠ В равен половине гипотенузы, т. е. АС = 12 АВ или АВ = 2АС.
По условию АС + АВ = 18см, значит АС + 2АС = 18см. Отсюда 3АС = 18см, АС = 6см. Тогда АВ = 2АС = 2*6 = 12см. Ответ: АС = 6см, ВС = 12см.
Билет. 21
|
|
|
