 |
Билет. 6. Виды углов. 1. (п. 25)Прямаясназываетсясекущейк прямымаиb,если она пересекает их в двух точках. 2. (п.19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то
|
|
|
|
Билет. 6
1. (п. 3-4) Луч (полупрямая) –часть прямой, имеющая начало и не имеющая конца. Угол –это геометрическая фигура, которая состоит из двух лучей исходящих изодной вершины.
Вершина угла —это точка, в которой два луча берут начало. Стороны угла —это лучи, которые образуют угол.
Например, вершина угла — точка O. Стороны угла — OA и OB. Для обозначения угла в тексте используется символ: ∠ AOB.
Способы обозначения углов:
| 1. Одной заглавной | 2. Тремя заглавными латинскими буквами, которыми | 3. Двумя строчными |
| латинской буквой, | обозначены вершина и две точки, расположенные на | латинскими буквами. |
| указывающейего | сторонах угла. Угол: ∠ AOD. | Угол: ∠ fn |
| вершину. Угол: ∠ O. | ||
| Называть угол можно с любого края, но НЕ с | ||
| вершины. Угол с рисунка выше имеет два названия: | ||
| ∠ AOD и ∠ DOA. | ||
| Вершина угла должна всегда находиться в середине | ||
| названия!!! |
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора – транспортира. Для обозначения градусов в тексте используется символ: °, например ∠ В = 50°
Виды углов
| Вид угла | Размер в градусах | Пример |
| Прямой | Равен 90° | |
| Острый | Меньше 90° | |
| Тупой | Больше 90° | |
| Развернутый | Равен 180° | |
2. (п. 18) В равнобедренном треугольнике углы при основании равны.
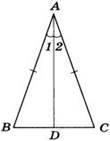Дано: ∆ АВС, АВ=АС.
Доказать, что∠ В=∠ С.
Доказательство: В∆ АВС из вершины А проведем биссектрису АД. ТреугольникиABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD – общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Ч. т. д.
|
|
|
3. Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна2100. Найдите все углы. Решение:
 |
Билет. 7
1. (п. 25)Прямаясназываетсясекущейк прямымаиb, если она пересекает их в двух точках.
При пересечении двух параллельных прямых секущей, образуются восемь углов, которые попарно называются:
1) 
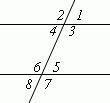соответственные углы (они попарно равны: ∠ 1 =∠ 5; ∠ 2 =∠ 6; ∠ 3 =∠ 7; ∠ 4 =∠ 8);
2) накрест лежащие углы (4 и 5; 3 и 6); они тоже попарно равны;
3) односторонние углы (3 и 5; 4 и 6); их сумма равна180°
(∠ 3 + ∠ 5 = 180°; ∠ 4 + ∠ 6 = 180°).
2. (п. 19) Если сторона и 2 прилежащих к ней угла одного треугольника соответственно равны стороне и 2 прилежащим к ней углам другого треугольника, то такие треугольники равны.
Дано: ∆ АВС и∆ А1В1С1, у них АВ=А1В1, ∠ А=∠ А1, ∠ В=∠ В1 Доказать, что∆ АВС= ∆ А1В1С1
Доказательство: Наложим∆ АВС на∆ А1В1С1так, чтобысторона АВ совпала со стороной А1В1 (по условию они равны, значит совпадут). Так как по условию ∠ А = ∠ А1 и ∠ В = ∠ В1, то сторона АС наложится на луч А1С1, а сторона ВС на луч В1С 1. Вершина С окажется лежащей как на луче А1С1, так и на луче В1С1, а значит совпадет с
вершиной С1. Все три точки у треугольников совпали, значит они равны. Ч. т. д.
3. АМ–биссектриса∆ АВС. Через точку М проведена прямая, параллельная АС и пересекающаясторону АВ в точке Е. Докажите, что ∆ АМЕ равнобедренный.
Доказательство: АС||ЕМ, значит∠ 1 =∠ 3 (как соответственные углы), ∠ 2 =∠ 4(как накрест лежащие углы), ∠ 1 = ∠ 2 (т. к. АМ – биссектриса).
Следовательно, ∠ 1 = ∠ 4, а это углы при основании в ∆ АМЕ, значит этот треугольник равнобедренный и АЕ = ЕМ. Ч. т. д.
|
|
|
Билет. 8
1. Постройте треугольник по 2 сторонам и углу между ними. Смотри презентацию, слайд 10.
2. (п. 30) Сумма углов в треугольнике 1800.
Дано: ∆ АВС.
Доказать, что∠ А+∠ В+∠ С= 1800.
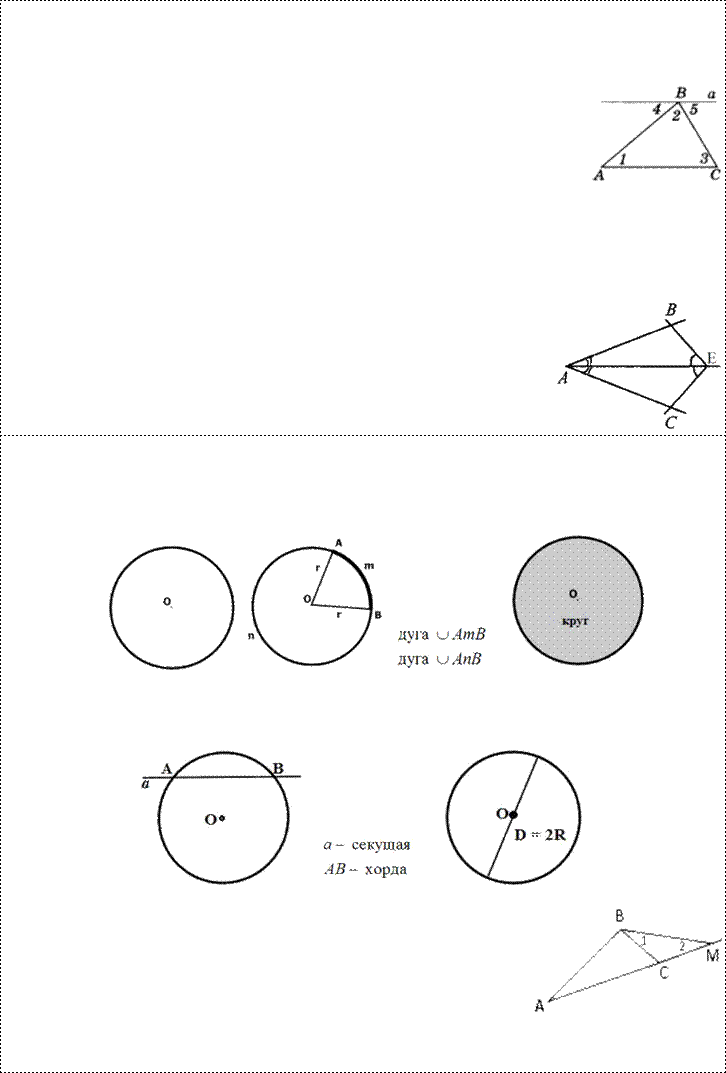
Доказательство: Проведем через вершину В прямую а, параллельную стороне АСОчевидно, что сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.
∠ 4 + ∠ 2 + ∠ 5 = 180° (*).
Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 – накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС.
Поэтому ∠ 4 = ∠ 1 = ∠ А, ∠ 5 = ∠ 3 = ∠ С. Отсюда, учитывая равенство (*), получаем: ∠ l + ∠ 2 + ∠ 3 = 180°,
или ∠ A + ∠ B + ∠ C = 180°. Ч. т. д.
3. На биссектрисе угла А взята точка Е, а на сторонах этого угла точки В и С так, что∠ АЕС=∠ АЕВ. Докажите, что ВЕ = СЕ.
Доказательство: Рассмотрим∆ АСЕ и∆ АВЕ.
У них: ∠ ВАЕ=∠ САЕ, т. к. АЕ – биссектриса угла А, ∠ АЕС = ∠ АЕВ (по условию). Сторона АЕ – общая.
Значит ∆ АСЕ = ∆ АВЕ по II признаку. Тогда ВЕ = СЕ. Ч. т. д.
|
|
|
