 |
Схемы замещения основных силовых элементов системы
|
|
|
|
Схема замещения является одним из средств, упрощающих представление об изучаемых процессах и облегчающих составление уравнений, которые описывают переходные процессы в электрической системе.
При составлении схем замещения элементы системы (генераторы, трансформаторы, линии электропередачи (ЛЭП) и т.д.) представляют простейшими элементами электрической цепи: индуктивностями, емкостями, активными сопротивлениями, проводимостями.
Схема замещения, положенная в основу математических операций, может рассматриваться в качестве некоторой логической или математической модели. Она может быть справедлива для любого момента времени и отражает связь между параметрами системы и параметрами режима только в какой-либо один характерный момент времени исследуемого процесса.
К составлению схем замещения, также как к объединению или упрощению изучаемой системы, нужно подходить весьма тщательно, так как неудачный выбор схемы замещения может привести к неточным или даже ошибочным результатам расчетов переходных процессов.
Рассмотрим схемы замещения некоторых элементов электрической системы.
Линии электропередачи.
Воздушные и кабельные линии напряжением 110 кВ и выше представляют, как и при расчетах установившихся режимов, Т-образной или П-образной схемой замещения (рис. 1.1).
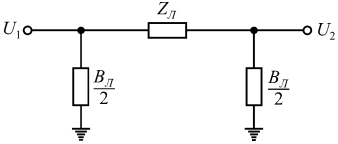
Рис. 1.1. П-образная схема замещения ЛЭП
На рис. 1.1 обозначено: 
; 
; 
; 
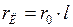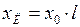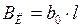, где 
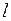- длина линии, км; 
, 
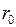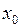- удельные активное и индуктивное сопротивления, Ом/км; 
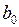- удельная емкостная проводимость, 1/Ом×км.
При упрощенном рассмотрении электромеханических переходных процессов линии электропередач могут замещаться полными 
или чисто индуктивными 
сопротивлениями.
|
|
|
Асинхронные двигатели при исследовании переходных процессов представляют известной схемой, отображающей основные контуры двигателя с учетом потерь.
Для расчетов, выявляющих количественные соотношения, рекомендуется пользоваться более точными схемами замещения.
Для анализа общих соотношений и оценки влияния процессов, происходящих в двигателе на систему, используют приближенную схему замещения, дающую завышение вращающего момента до 10 % (рис. 1.2, а) или даже схему замещения (рис. 1.2, б).
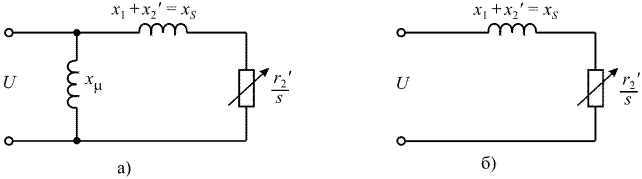
Рис. 1.2. Схемы замещения асинхронного двигателя
Трансформаторы. При расчетах электромеханических переходных процессов схемы замещения трансформаторов представляют Г-образной схемой с учетом ветви намагничивания. Часто в расчетах ветвь намагничивания не учитывают и трансформатор представляется чисто индуктивным сопротивлением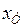 
(двухобмоточный трансформатор) или многолучевой звездой индуктивных сопротивлений в случае многообмоточного трансформатора.
Синхронные машины (генераторы, двигатели) при уточненных расчетах представляются комплексными схемами замещения. При упрощенных расчетах - индуктивными сопротивлениями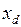 
, 
, 
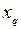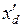, за которыми находятся соответственно ЭДС 
, 
, 
, (
).
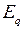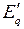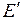Математическое описание электромеханических
Переходных процессов
Рассмотрим простейшую электрическую систему "генератор-шины", представляющую эквивалентный блок синхронный генератор-трансформатор, соединенный линией электропередачи с шинами приемной системы бесконечной мощности (шинами неизменного напряжения). Шинами бесконечной мощности называют шины приемной системы, мощность которой в 5 и более раз превышает мощность удаленной станции. Напряжение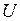 
на шинах приемной системы (подстанции) во всех режимах остается неизменным, а вектор напряжения вращается с синхронной частотой 
.
|
|
|
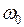При составлении схемы замещения электрической системы все ее элементы, учитывая выше отмеченные допущения, представляют только индуктивными сопротивлениями. Электрическую систему, представленную такой схемой замещения и при постоянстве напряжения приемной системы, называют идеализированной. Расчетная схема такой системы и ее схема замещения представлены на рис. 1.3, а, б.
На схеме замещения обозначено следующее:
, 
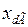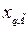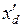, - синхронные по осям 
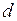и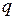 
и переходное сопротивление генератора (каталожные данные);
, 
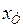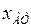- индуктивные сопротивления трансформатора и автотрансформатора;
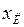- сопротивление одной цепи линии;
, , 
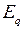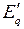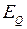- синхронная, переходная и фиктивная ЭДС генератора;
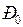- мощность турбины;
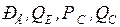- активная и реактивная мощности, выдаваемые генератором и поступающие в систему соответственно. В нормальном режиме 
.
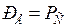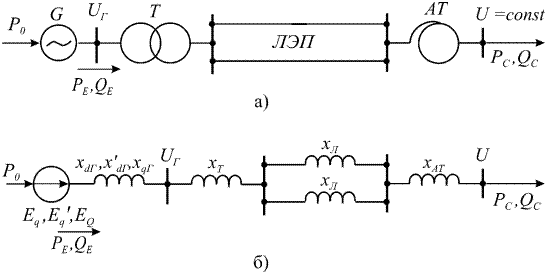
Рис. 1.3. Расчетная схема (а) и схема замещения (б) простейшей системы
Обозначим: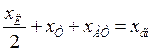 
- внешнее сопротивление системы;
, 
, 
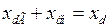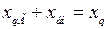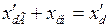- суммарные синхронные по осям 
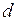и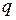 
и суммарное переходное сопротивление системы.
Схема замещения после преобразования примет вид, приведенный на рис. 1.4.
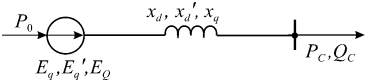
Рис. 1.4. Упрощенная схема замещения системы
На рис. 1.5 изображена видоизмененная схема замещения системы при представлении генератора за сопротивлением 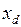. Здесь показаны вектор напряжения системы 
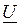, вращающийся с синхронной частотой вращения 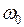и вектор ЭДС 
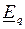, совпадающий с поперечной осью 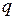, которая жестко связана с ротором генератора. В общем случае частота вращения ротора 
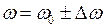. Фазовый угол 
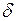- угол между вектором напряжения 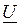и вектором ЭДС 
(угол электропередачи).
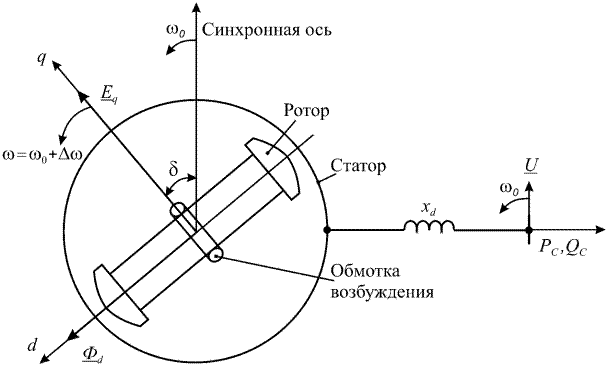
Рис. 1.5. Видоизмененная схема замещения системы
В зависимости от поставленной задачи расчеты электромеханических переходных процессов в электрических системах проводят по полным или упрощенным уравнениям Парка-Горева. В инженерных расчетах часто используют упрощенную математическую модель, то есть в уравнениях Парка-Горева, записанных в осях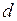 
и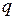 
, жестко связанных с ротором генератора, не учитывают переходные процессы в статорной цепи, то есть ЭДС трансформации и ЭДС вращения; активное сопротивление цепи статора, то есть апериодическую составляющую тока статора и периодическую составляющую обмотки возбуждения; переходные процессы в демпферных контурах ротора генератора.
|
|
|
После принятых упрощений системы дифференциальных уравнений простейшей системы согласно схем замещения, приведенных на рисунках 4 и 5, имеет вид:
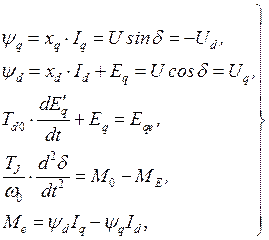(1.1)
где 1-е и 2-е уравнения системы определяют связь между параметрами режима цепи статора генератора по продольной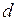 
и поперечной 
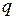осям; 3-е уравнение - уравнение переходных процессов в обмотке возбуждения; 4-е уравнение - уравнение относительного движения ротора генератора (подробно об этом уравнении см. ниже); 5-е - выражение электромагнитного момента.
В (1) обозначено:
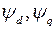- результирующие потокосцепления обмотки статора по осям 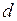и 
;
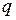- проекции напряжения системы на оси 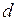и ;
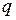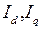- проекции тока генератора на оси 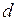и ;
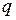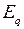- синхронная ЭДС или ЭДС возбуждения, пропорциональная току возбуждения генератора;
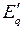- проекция переходной ЭДС генератора 
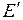, величина которой пропорциональна результирующему потокосцеплению обмотки возбуждения и обладает всеми свойствами этого потокосцепления;
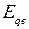- вынужденная ЭДС, пропорциональная изменению напряжения возбуждения, а в установившемся режиме (режиме, предшествовавшем возмущению) равна синхронной ЭДС установившегося режима, = 
;
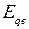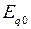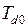- постоянная времени обмотки возбуждения при разомкнутой статорной обмотке;
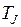- инерционная постоянная агрегата;
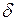- угол между вектором напряжения системы 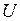и вектором ЭДС 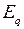, жестко связанной с осью 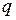и с ротором (фазовый угол);
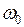- синхронная частота вращения;
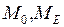- моменты турбины и электромагнитный момент генератора.
Как было отмечено выше, при частоте вращения ротора, близкой к синхронной (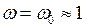
), примерно так характеризуется переходный процесс, в относительных единицах моменты приблизительно равны мощностям. Замена в уравнении движения величин моментов на мощности (
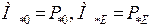) упрощает расчеты переходных процессов, так как величину электромагнитной мощности можно определить по измерениям токов и напряжений, тогда как измерение величины электромагнитного момента достаточно сложно.
|
|
|
После преобразований уравнения движения система уравнений переходных процессов простейшей системы принимает вид:
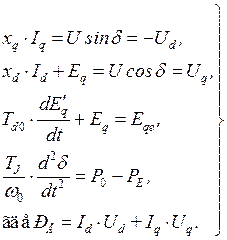(1.2)
В выражении (1.2) все токи, ЭДС, мощности выражены в о.е., постоянные времени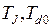 
- в секундах, угол 
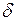- в радианах, 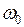- в рад/с, время 
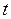- в секундах.
Для установившегося режима работы электрической системы все режимные параметры постоянны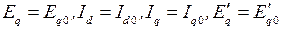 
, 
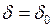. Учитывая, что производные от постоянных величин равны нулю, система (2) для установившегося режима может быть записана в виде следующей системы уравнений:
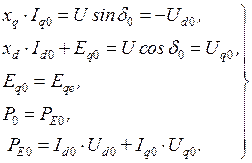(1.3)
|
|
|
