 |
Угловые характеристики активной и реактивной мощности генераторов в многомашинной системе
|
|
|
|
Выражения для определения активных и реактивных мощностей, токов и напряжений в любом элементе линейной системы при установившемся режиме или очень медленном его изменении находятся с помощью метода наложения. Для этого необходимо, чтобы все синхронные машины были представлены некоторыми постоянными сопротивлениями с приложенными к ним ЭДС, а синхронные двигатели нагрузки – некоторыми пассивными элементами. Такое простое представление генераторов и двигателей возможно и для переходных процессов, но только для какого-то одного момента времени. Однако полученные упрощенные соотношения, называемые обычно статическими характеристиками, иногда применяют и для достаточно больших интервалов времени переходного процесса.
Любая система может быть в этом случае представлена схемой, аналогичной схеме, показанной на рис. 2.9. Пользуясь методом наложения, заменяем рассмотрение этой схемы последовательным рассмотрением подсхем, представленных на рис. 2.10. Этих подсхем должно быть столько, сколько в схеме (рис. 2.9) имеется ветвей, содержащих ЭДС. Согласно этому методу наложения, ток в любой ветви
,
где 
собственный ток; 
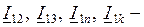взаимные токи.
Рис. 2.9. Схема замещения сложной системы
Под собственным током понимается составляющая тока в любой ветви, вызванная действием ЭДС, приложенной в данной ветви при отсутствии (равенстве нулю) ЭДС в других ветвях. Под взаимным током понимается составляющая тока в какой-либо ветви, вызванная действием ЭДС в другой ветви при равенстве нулю ЭДС во всех остальных ветвях.
Очевидно, что 
,
где 
собственная проводимость, определяющая величину и фазу составляющей тока от действия ЭДС в данной ветви при ЭДС во всех остальных ветвях, равных нулю, например 
.
|
|
|
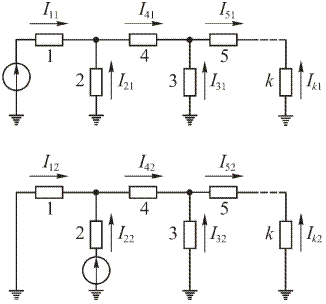
Рис. 2.10. Подсхемы, применяемые при анализе по методу наложения
Аналогично,
,
где 
взаимная проводимость, определяющая величину и фазу тока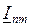 
в ветви n от действия ЭДС, приложенной в ветви m, при равенстве нулю ЭДС во всех остальных ветвях, например 
.
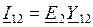Собственные и взаимные проводимости для любой схемы легко находятся или способом преобразований, или способом единичных токов.
При способе преобразований любая схема (например, см. рис. 2.9) приводится к виду схемы, показанной на рис. 2.11. Исходя из преобразованной схему, легко найти взаимные проводимости:
и т.д.
Рис. 2.11. Схема замещения системы для определения
собственных и взаимных проводимостей
И собственные проводимости, например
.
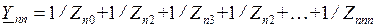Величины, обратные собственным проводимостям, называются собственными сопротивлениями, а величины, обратные взаимным проводимостям, - взаимными сопротивлениями.
При применении способа единичных токов для определения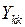 
, то есть собственной проводимости какой-либо ветви k, и взаимной ее проводимости с ветвью 
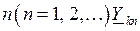поступают следующим образом. Предполагают, что к ветви k приложена некая расчетная ЭДС 
, величина и фаза которой приняты такими, что в ветви n от действия только этой ЭДС (при равных нулю ЭДС во всех остальных ветвях) протекает ток 
. Зная величину тока в ветви n, находим, что падение напряжения в ней
.
Очевидно, что напряжение, приложенное в точке присоединения 
равно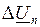 
.
Производя далее токораспределение, находим токи и напряжения во всех ветвях и в конечном счете величины тока 
и ЭДС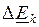 
. При этом взаимная проводимость 
, а собственная проводимость 
. В связи с определением этих проводимостей напомним, что для индуктивной цепи
,
где
; 
,
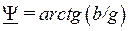соответственно
.
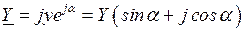Здесь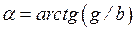 
, причем знак угла 
в общем случае зависит от знаков слагающих g и b.
|
|
|
При определении взаимной проводимости часто получают отрицательные значения ее вещественной составляющей, то есть – g, и соответственно для угла 
, то есть отрицательные значения. Это может вызвать недоумение, так как у какого-либо реального элемента отрицательная составляющая проводимости может быть только в активной схеме (при наличии в этом элементе источника энергии). Однако взаимная проводимость не характеризует реальный элемент, а представляет собой некоторый комплексный коэффициент пропорциональности между током в одной ветви схемы и напряжением в другой ветви. Поэтому она может иметь отрицательную вещественную составляющую и в пассивных схемах. У собственных проводимостей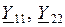 
, определяемых как отношение тока к напряжению в данной точке схемы, активные составляющие не могут быть отрицательными, если только отдельные ветви схемы сами по себе не содержат отрицательных активных сопротивлений, то есть некоторых источников мощности, наличие которых в данном случае из рассмотрения исключается. Таким образом, углы 
и 
собственных проводимостей и их вещественные составляющие всегда положительны; угол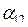 
может быть как положительным, так и отрицательным.
Определение собственных и взаимных проводимостей не представляет затруднений для любой сколь угодно сложной системы. Однако большинство расчетов, проводимых для определения распределения токов, напряжений, мощностей, в особенности расчетов статической и динамической устойчивости, требует упрощения расчетных схем электрической системы.
Комплекс полной мощности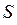 
, протекающей через какую-либо точку схемы, определяется как произведение прямого комплекса ЭДС или напряжения, действующего в данной точке, на сопряженный комплекс тока.
Например, мощность, выдаваемая источником ветви.
, (2.38)
Рис. 2.12. Векторная диаграмма системы из трех станций
Преобразуем выражение для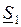 
:
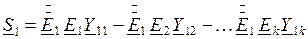. (2.39)
Примем 
, то есть выберем ось отсчета, совпадающую с направлением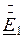 
(рис. 2.12); ЭДС с 
, 
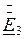и т.д. Представим как
Условно предполагая, что все они отстают от 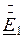. Тогда
(2.40)
Записав все действительные и мнимые части комплекса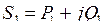 
, получим выражение для активной мощности
|
|
|
(2.41)
или в общем случае
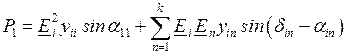. (2.42)
Для реактивной мощности соответственно
;
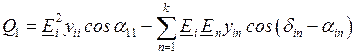. (2.43)
|
|
|
