 |
И соотношения, получаемые из векторной диаграммы
|
|
|
|
Рассмотрим простейшую систему, схема замещения которой представлена на рис. 2.1.

Рис. 2.1. Схема замещения системы
Режим данной системы характеризуется напряжением  на шинах системы, активной
на шинах системы, активной  и реактивной
и реактивной  мощностями в начале и в конце электропередачи, напряжением на зажимах генератора
мощностями в начале и в конце электропередачи, напряжением на зажимах генератора  и одной из ЭДС
и одной из ЭДС  ,
,  .
.
Рассмотрим физический смысл этих ЭДС и их использование при расчетах установившихся режимов и переходных процессов.
ЭДС холостого хода (синхронная ЭДС)  обуславливается током возбуждения генератора. В машине с нерегулируемым возбуждением она остается постоянной при любых медленных изменениях режима. Поэтому в тех случаях, когда требуется рассчитать ряд режимов при неизменном токе возбуждения, удобно генераторы вводить в расчетную схему синхронным реактивным сопротивлением
обуславливается током возбуждения генератора. В машине с нерегулируемым возбуждением она остается постоянной при любых медленных изменениях режима. Поэтому в тех случаях, когда требуется рассчитать ряд режимов при неизменном токе возбуждения, удобно генераторы вводить в расчетную схему синхронным реактивным сопротивлением  и ЭДС
и ЭДС  , включенным за этим сопротивлением. При резких изменениях режима ЭДС
, включенным за этим сопротивлением. При резких изменениях режима ЭДС  также резко изменяется, повторяя изменение тока ротора.
также резко изменяется, повторяя изменение тока ротора.
ЭДС  , которая называется переходной, обусловлена результирующим полным потокосцеплением обмотки возбуждения. Поперечная составляющая этой ЭДС
, которая называется переходной, обусловлена результирующим полным потокосцеплением обмотки возбуждения. Поперечная составляющая этой ЭДС  (проекция вектора
(проекция вектора  на ось
на ось  машины согласно векторной диаграммы) обладает примечательным свойством - остается неизменной в момент резких изменений режима синхронной машины. Эта ЭДС является расчетной величиной. Она широко применяется при расчетах переходных процессов, поскольку ее неизменность в момент возмущения некоторого исходного установившегося режима позволяет связать параметры режима системы, предшествовавшего нарушению, с параметрами режима, возникшего после нарушения. Вместе с тем ЭДС
машины согласно векторной диаграммы) обладает примечательным свойством - остается неизменной в момент резких изменений режима синхронной машины. Эта ЭДС является расчетной величиной. Она широко применяется при расчетах переходных процессов, поскольку ее неизменность в момент возмущения некоторого исходного установившегося режима позволяет связать параметры режима системы, предшествовавшего нарушению, с параметрами режима, возникшего после нарушения. Вместе с тем ЭДС  , а также близкая ей по величине переходная
, а также близкая ей по величине переходная  , с успехом могут быть использованы и при приближенных расчетах установившихся режимов системы, генераторы которой снабжены автоматическими регуляторами возбуждения пропорционального действия (АРВ п.д.). В этом случае генераторы вводят в схему замещения неизменной ЭДС
, с успехом могут быть использованы и при приближенных расчетах установившихся режимов системы, генераторы которой снабжены автоматическими регуляторами возбуждения пропорционального действия (АРВ п.д.). В этом случае генераторы вводят в схему замещения неизменной ЭДС 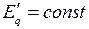 за переходным сопротивлением
за переходным сопротивлением  . Для расчетов режима при этом в качестве неизменной величины может быть принята также ЭДС
. Для расчетов режима при этом в качестве неизменной величины может быть принята также ЭДС  .
.
|
|
|
Результаты расчетов установившихся режимов в обоих случаях будут близкими, т.к. значения ЭДС  и
и  в таких режимах различаются незначительно. Использование ЭДС
в таких режимах различаются незначительно. Использование ЭДС  в расчетах приводит к более простым формулам, поскольку эта ЭДС непосредственно может быть включена в схему замещения системы. Благодаря этому имеется возможность ввести в расчетную схему синхронный генератор реактивным сопротивлением
в расчетах приводит к более простым формулам, поскольку эта ЭДС непосредственно может быть включена в схему замещения системы. Благодаря этому имеется возможность ввести в расчетную схему синхронный генератор реактивным сопротивлением  и неизменной ЭДС
и неизменной ЭДС  (
( ), включенной за этим сопротивлением.
), включенной за этим сопротивлением.
ЭДС  непосредственно из схемы замещения определена быть не может. Она получается на основе векторной диаграммы, что приводит к некоторому усложнению расчета системы. Однако при этом достигается определенный положительный результат. Векторная диаграмма позволяет установить, что вектор ЭДС
непосредственно из схемы замещения определена быть не может. Она получается на основе векторной диаграммы, что приводит к некоторому усложнению расчета системы. Однако при этом достигается определенный положительный результат. Векторная диаграмма позволяет установить, что вектор ЭДС  имеет тот же аргумент (угол
имеет тот же аргумент (угол  ), что и ЭДС
), что и ЭДС  . Выше было отмечено (см. рис. 1.5), что угол
. Выше было отмечено (см. рис. 1.5), что угол 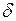 , определяющий фазу ЭДС
, определяющий фазу ЭДС  , характеризует также и положение оси
, характеризует также и положение оси  вращающегося ротора синхронного генератора относительно синхронно вращающейся оси. При расчетах простейшей системы удобно эту ось совместить с вектором неизменного напряжения на шинах приемной системы. В этих условиях любые изменения фазы ЭДС
вращающегося ротора синхронного генератора относительно синхронно вращающейся оси. При расчетах простейшей системы удобно эту ось совместить с вектором неизменного напряжения на шинах приемной системы. В этих условиях любые изменения фазы ЭДС  будут определять аналогичные изменения взаимного расположения вращающегося ротора генератора на удаленной станции и вектора напряжения приемной системы
будут определять аналогичные изменения взаимного расположения вращающегося ротора генератора на удаленной станции и вектора напряжения приемной системы  . Такой же вывод может быть сделан при выполнении расчетов с использованием ЭДС
. Такой же вывод может быть сделан при выполнении расчетов с использованием ЭДС  .
.
Напряжение генератора  для рассматриваемой схемы замещения принимается в расчетах приложенным за сопротивлением генератора
для рассматриваемой схемы замещения принимается в расчетах приложенным за сопротивлением генератора  = 0. О фиктивной ЭДС
= 0. О фиктивной ЭДС 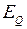 будет отмечено ниже.
будет отмечено ниже.
|
|
|
Соотношения между параметрами режима (ЭДС, напряжениями, токами, фазовыми углами) в наглядной форме могут быть получены с помощью векторных диаграмм синхронной машины. Векторная диаграмма дает количественную оценку параметров режима в определенные моменты времени 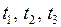 и т.д. установившегося режим. Таким образом построение векторной диаграммы тесно связано с расчетом установившегося режима работы системы.
и т.д. установившегося режим. Таким образом построение векторной диаграммы тесно связано с расчетом установившегося режима работы системы.
Для начала рассмотрим явнополюсную синхронную машину (гидрогенератор, синхронный компенсатор). Здесь из-за магнитной несимметрии ротора в продольной 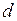 и поперечной
и поперечной  осях имеют место различные, обусловленные токами реакции статора, потоки, замыкающиеся через сталь ротора, когда последний занимает относительно магнитной оси фазы продольное и поперечное положения. В конечном итоге для явнополюсных машин несимметрия выражается различием синхронных индуктивных сопротивлений по осям
осях имеют место различные, обусловленные токами реакции статора, потоки, замыкающиеся через сталь ротора, когда последний занимает относительно магнитной оси фазы продольное и поперечное положения. В конечном итоге для явнополюсных машин несимметрия выражается различием синхронных индуктивных сопротивлений по осям  и
и  -
-  и
и  .
.
Если условно допустить, что индуктивные сопротивления машины в обеих осях одинаковы и равны 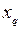 , то явнополюсная машина может быть заменена эквивалентной неявнополюсной машиной с
, то явнополюсная машина может быть заменена эквивалентной неявнополюсной машиной с  и некоторой фиктивной ЭДС
и некоторой фиктивной ЭДС 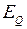 .
.
Значение 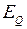 представляет собой часть синхронной ЭДС, то есть ЭДС, обусловленной возбуждением
представляет собой часть синхронной ЭДС, то есть ЭДС, обусловленной возбуждением  , и не отражает степень возбуждения машины, но вектор
, и не отражает степень возбуждения машины, но вектор  совпадает, как и вектор
совпадает, как и вектор  с поперечной осью ротора генератора. Это позволяет точно определить угол
с поперечной осью ротора генератора. Это позволяет точно определить угол  между вектором напряжения системы и осью
между вектором напряжения системы и осью  . Следует иметь ввиду, что замещение явнополюсной машины ЭДС
. Следует иметь ввиду, что замещение явнополюсной машины ЭДС  , приложенной за сопротивлением
, приложенной за сопротивлением  не позволяет определить угол
не позволяет определить угол  .
.
Таким образом, явнополюсный генератор в расчетах установившегося режима представляется фиктивной ЭДС 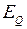 за поперечной синхронной реактивностью
за поперечной синхронной реактивностью  . Связь между
. Связь между 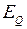 и
и  можно получить из векторной диаграммы. Для построения векторной диаграммы и определения параметров установившегося режима простейшей системы с явнополюсным синхронным генератором используем первые 2 уравнения системы (1.3), приняв
можно получить из векторной диаграммы. Для построения векторной диаграммы и определения параметров установившегося режима простейшей системы с явнополюсным синхронным генератором используем первые 2 уравнения системы (1.3), приняв  ,
, 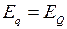
 (2.1)
(2.1)
Умножив 1-е уравнение на  и сложив его со вторым, получим:
и сложив его со вторым, получим:
|
|
|
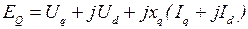
или, более сокращенно
 . (2.2)
. (2.2)
Соотношение (2.2) представляет обобщенный закон Ома для участка сети. Таким образом, используя ЭДС 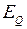 , можно представить синхронную машину в установившемся режиме ее работы в виде ЭДС, включенной за сопротивлением
, можно представить синхронную машину в установившемся режиме ее работы в виде ЭДС, включенной за сопротивлением  .
.
Для определения ЭДС 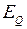 и других режимных параметров и для построения векторной диаграммы выбирают количество известных параметров режима по формуле:
и других режимных параметров и для построения векторной диаграммы выбирают количество известных параметров режима по формуле:
 ,
,
где  - количество машин (электрических станций) в системе,
- количество машин (электрических станций) в системе,
 - количество известных параметров.
- количество известных параметров.
Для простейшей системы, в нашем случае,  = 1,
= 1,  = 3. Это могут быть
= 3. Это могут быть  - напряжение шин системы, активная
- напряжение шин системы, активная  и реактивная
и реактивная  мощности, выдаваемые в систему,
мощности, выдаваемые в систему,  и т.п. Для двухмашинной системы
и т.п. Для двухмашинной системы  = 5, трехмашинной -
= 5, трехмашинной -  = 7 и т.д.
= 7 и т.д.
В нашем случае для простейшей системы примем за известные параметры  . Очевидно, что выражение (2.1), записанное при использовании комплексной плоскости, вещественная ось которой совмещена с осью
. Очевидно, что выражение (2.1), записанное при использовании комплексной плоскости, вещественная ось которой совмещена с осью  , а мнимая - с осью
, а мнимая - с осью 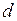 , будет справедливо при любом другом положении осей комплексной плоскости. В частности, удобно совместить вектор напряжения
, будет справедливо при любом другом положении осей комплексной плоскости. В частности, удобно совместить вектор напряжения 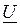 с вещественной осью новой комплексной плоскости
с вещественной осью новой комплексной плоскости  . По известным
. По известным  и
и 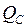 можно определить величину и положение вектора тока относительно вектора напряжения (рис. 2.2):
можно определить величину и положение вектора тока относительно вектора напряжения (рис. 2.2):
 . (2.3)
. (2.3)
Следует заметить, что в соответствии с расположением векторов тока и напряжения на комплексной плоскости следует принять  . Подставив (2.3) в (2.2) получим выражение вида
. Подставив (2.3) в (2.2) получим выражение вида
 . (2.4)
. (2.4)
Очевидно, что модуль фиктивной ЭДС 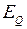 может быть найден с помощью следующей формулы
может быть найден с помощью следующей формулы
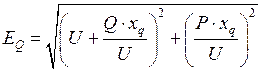 . (2.5)
. (2.5)
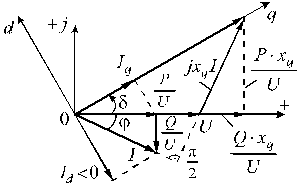
Рис. 2.2. Векторная диаграмма для определения величины и направления ЭДС 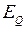
Аргумент ЭДС (фазовый угол  ) определится как
) определится как
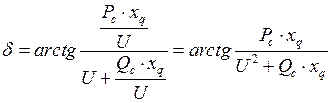 . (2.6)
. (2.6)
После нахождения величины и положения на комплексной плоскости ЭДС 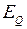 , а, следовательно, и направление поперечной оси
, а, следовательно, и направление поперечной оси  ротора синхронной машины, могут быть найдены
ротора синхронной машины, могут быть найдены  - составляющие всех переменных. Кроме того проекции тока
- составляющие всех переменных. Кроме того проекции тока  на оси
на оси  и
и  -
-  и
и  могут быть определены из (2.1). Приняв, что
могут быть определены из (2.1). Приняв, что  , а
, а  , согласно (1.3), то есть
, согласно (1.3), то есть
|
|
|
 . (2.7)
. (2.7)
Токи  и
и  (рис. 2.2) можно рассматривать как активный и реактивный токи по отношению к ЭДС
(рис. 2.2) можно рассматривать как активный и реактивный токи по отношению к ЭДС 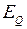 . При принятых положительных направлениях осей
. При принятых положительных направлениях осей  и
и  (аналогичных направлению осей
(аналогичных направлению осей  и
и  на комплексной плоскости) ток
на комплексной плоскости) ток  положителен в генераторном режиме, а реактивная составляющая тока - ток
положителен в генераторном режиме, а реактивная составляющая тока - ток  , при индуктивной нагрузке (
, при индуктивной нагрузке ( ) соответствует отрезку, который направлен против оси
) соответствует отрезку, который направлен против оси  отрицателен (
отрицателен (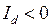 ). Сказанное подтверждается и соотношениями (2.7).
). Сказанное подтверждается и соотношениями (2.7).
Используя вышеизложенное, рассмотрим порядок построения векторной диаграммы электропередачи и получим из нее соотношения, применяемые при расчетах переходных процессов электрической системы (рис. 2.3).
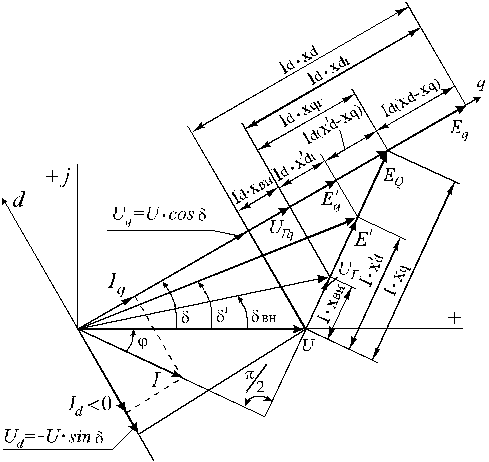
Рис. 2.3. Векторная диаграмма простейшей электрической системы
Построение начинают с совмещения вектора напряжения системы  с вещественной осью комплексной плоскости. Далее определяется направление осей
с вещественной осью комплексной плоскости. Далее определяется направление осей  и
и  . Ось
. Ось  направлена под фазовым углом
направлена под фазовым углом  , определяемым по выражению (2.6). От начала координат откладывают величину
, определяемым по выражению (2.6). От начала координат откладывают величину 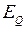 , полученную из (2.5). Отложив от конца вектора
, полученную из (2.5). Отложив от конца вектора 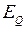 величину
величину  (ток
(ток  отрицателен), получим значение синхронной ЭДС
отрицателен), получим значение синхронной ЭДС  , то есть величину, пропорциональную току возбуждения явнополюсной синхронной машины.
, то есть величину, пропорциональную току возбуждения явнополюсной синхронной машины.
Таким образом, синхронная ЭДС  явнополюсного генератора можно определить по выражению:
явнополюсного генератора можно определить по выражению:
 (2.8)
(2.8)
Откладывая от конца вектора 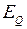 в сторону начала координат отрезок
в сторону начала координат отрезок 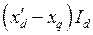 , определим длину вектора
, определим длину вектора  - проекцию вектора переходной ЭДС
- проекцию вектора переходной ЭДС 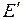 на ось
на ось  . Комплексы переходной ЭДС
. Комплексы переходной ЭДС  и напряжение на зажимах генератора
и напряжение на зажимах генератора  можно записать аналогично выражению (2.4)
можно записать аналогично выражению (2.4)
 . (2.9)
. (2.9)
 . (2.10)
. (2.10)
Положения этих векторов представлены на рис. 2.3. Выражение для модулей и аргументов соответственно имеют вид:
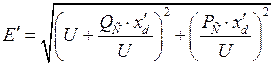 , (2.11)
, (2.11)
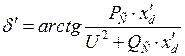 , (2.12)
, (2.12)
 , (2.13)
, (2.13)
 . (2.14)
. (2.14)
Следует отметить, что формулы (2.5), (2.11), (2.13) имеют одинаковую структуру и полностью подобны формулам, определяющим связь между напряжениями в начале и конце линии электропередачи, отличающимися продольной и поперечной составляющими падения напряжения.
Для неявнополюсной синхронной машины (турбогенератор) синхронные сопротивления по осям  и
и  одинаковы
одинаковы  и фиктивная ЭДС
и фиктивная ЭДС  равна синхронной ЭДС
равна синхронной ЭДС  , то есть
, то есть  =
=  . Тогда выражение для определения синхронной ЭДС
. Тогда выражение для определения синхронной ЭДС  неявнополюсной синхронной машины (турбогенератор, синхронный турбодвигатель) будет иметь вид
неявнополюсной синхронной машины (турбогенератор, синхронный турбодвигатель) будет иметь вид
 , (2.15)
, (2.15)
 . (2.16)
. (2.16)
Из векторной диаграммы простейшей электрической системы могут быть получены также и следующие очевидные соотношения.
|
|
|
Продольная составляющая напряжения на зажимах генератора
 . (2.17)
. (2.17)
Продольная составляющая переходной ЭДС
 . (2.18)
. (2.18)
Продольная  и поперечная
и поперечная  составляющие тока статора:
составляющие тока статора:
 , (2.19)
, (2.19)
 , (2.20)
, (2.20)
где  .
.
Полный ток статора генератора:
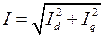 . (2.21)
. (2.21)
Активная мощность, выдаваемая генератором:
 , (2.22)
, (2.22)
реактивная мощность, выдаваемая генератором:
 . (2.23)
. (2.23)
В ряде практических случаев оказывается необходимым устанавливать взаимную связь между ЭДС  . Подставив в (2.8) значение тока
. Подставив в (2.8) значение тока  из (2.7), получим связь между
из (2.7), получим связь между  и
и  для явнополюсной машины (гидрогенератора):
для явнополюсной машины (гидрогенератора):
 . (2.24)
. (2.24)
Из векторной диаграммы (рис. 2.3) можно получить:
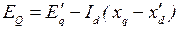 . (2.25)
. (2.25)
Решая совместно (2.8) и (2.25), получаем связь между ЭДС  и
и  :
:
 . (2.26)
. (2.26)
|
|
|


