 |
Определение токов синхронных машин
|
|
|
|
По аналогии с простейшей системой для нахождения токов каждой из машин (станций) могут быть использованы выражения (2.21)-(2.23)
 ,
,
где  , если рассчитываются токи и мощности для явнополюсных машин (ГГ, СК, СД);
, если рассчитываются токи и мощности для явнополюсных машин (ГГ, СК, СД);  , если рассчитываются токи и мощности для неявнополюсных машин (ТГ, турбодвигатели).
, если рассчитываются токи и мощности для неявнополюсных машин (ТГ, турбодвигатели).
В общем виде, используя выражения (2.42) и (2.43):
 , (2.44)
, (2.44)
 . (2.45)
. (2.45)
Полный ток  -го генератора
-го генератора
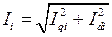 . (2.46)
. (2.46)
Выражения (2.42)-(2.45) универсальны. С их помощью можно определить токи и мощности любой сложности, в том числе и простейшей. При неучете активных сопротивлений в элементах схемы собственные и взаимные углы потерь равны нулю ( ). Если какой-то узел схемы является не генератором, а приемником электроэнергии с напряжением
). Если какой-то узел схемы является не генератором, а приемником электроэнергии с напряжением  , то в этом случае знаки перед слагаемыми в выражениях (2.42)-(2.45) необходимо изменить на обратные, а соответствующую ЭДС заменить на напряжение
, то в этом случае знаки перед слагаемыми в выражениях (2.42)-(2.45) необходимо изменить на обратные, а соответствующую ЭДС заменить на напряжение  .
.
Статические характеристики и регулирующие
Эффекты нагрузки
Статические характеристики нагрузок отражают изменение потребляемой узлом активной и реактивной мощностей при изменении напряжения  и частоты
и частоты 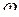 . Каждая точка любой характеристики отвечает определенному установившемуся режиму. Характеристики могут быть представлены в виде
. Каждая точка любой характеристики отвечает определенному установившемуся режиму. Характеристики могут быть представлены в виде
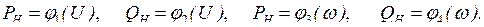
Эти характеристики, как правило, нелинейны. Но в расчетной практике и в экспериментах часто приходится иметь дело с малыми отклонениями 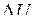 и
и  от нормальных значений. Этим отклонениям соответствуют значения
от нормальных значений. Этим отклонениям соответствуют значения  ,
,  , полученные при линеаризации статических характеристик. По значениям
, полученные при линеаризации статических характеристик. По значениям 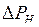 и
и  могут быть вычислены регулирующие эффекты активной и реактивной мощности нагрузки:
могут быть вычислены регулирующие эффекты активной и реактивной мощности нагрузки:
|
|
|
· по напряжению при постоянной частоте
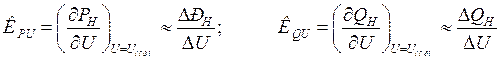 ;
;
· по частоте при постоянном напряжении
 .
.
Регулирующие эффекты выражаются в относительных единицах, например, для 
 .
.
Таким образом, регулирующий эффект нагрузки показывает степень изменения активной или реактивной мощностей нагрузки от нормального при изменении напряжения на ее выводах или частоты от нормальных. В расчетах обычно принимают нормальные значения напряжения и частоты за номинальные  . Рассмотрим статические характеристики и регулирующие эффекты различных видов нагрузок. Простейшим видом нагрузки являются постоянные активные, индуктивные и емкостные сопротивления (рис. 2.13). Здесь активная и реактивная мощности нагрузки пропорциональна квадрату напряжения и статические характеристики представляют вид парабол:
. Рассмотрим статические характеристики и регулирующие эффекты различных видов нагрузок. Простейшим видом нагрузки являются постоянные активные, индуктивные и емкостные сопротивления (рис. 2.13). Здесь активная и реактивная мощности нагрузки пропорциональна квадрату напряжения и статические характеристики представляют вид парабол:  .
.
Регулирующие эффекты нагрузок определим в относительных единицах при номинальных базисных условиях параметров узла ( ) в нормальном режиме.
) в нормальном режиме.
|

Рис. 2.13. Представление различных нагрузок постоянным активным сопротивлением (а), постоянным индуктивным сопротивлением (б),
постоянным емкостным сопротивлением (в)
Для активной нагрузки (рис. 2.13, а):
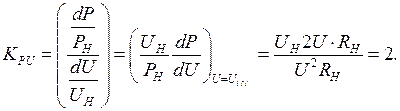
Получено, что регулирующий эффект активной мощности нагрузки по напряжению  , то есть при снижении или повышении напряжения в узле нагрузки на 1 % активная мощности нагрузки, представленная постоянным активным сопротивлением соответственно снизится или повысится на 2 %. В этом случае
, то есть при снижении или повышении напряжения в узле нагрузки на 1 % активная мощности нагрузки, представленная постоянным активным сопротивлением соответственно снизится или повысится на 2 %. В этом случае  .
.
При других показателях степени  напряжения
напряжения  ,
,  .
.

Таким образом, регулирующий эффект нагрузки численно равен показателю степени у параметра, по которому определяется регулирующий эффект нагрузки. Например, мощность, потребляемая лампами накаливания, определяют по выражению  , следовательно
, следовательно  .
.
Нагрузка представлена индуктивным сопротивлением (рис. 2.13, б). В этом случае
 .
.
Регулирующие эффекты будут равны
|
|
|
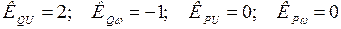 .
.
Нагрузка представлена емкостью, например, конденсаторная батарея для поперечной емкостной компенсации (рис. 2.13, в). Конденсаторы отдают ("генерируют") реактивную мощность в сеть, следовательно, получаемая батареей мощность отрицательна:
 .
.
При отрицательной мощности 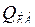 , регулирующий эффект
, регулирующий эффект  также отрицателен
также отрицателен  .
.
Таким образом, характеристики конденсаторов с точки зрения поддержания напряжения в узле при изменении режимов работы электрической сети неблагоприятны, особенно при коротких замыканиях в сети (при снижении напряжения в узле потребление  увеличивается, обуславливая дальнейшее снижение
увеличивается, обуславливая дальнейшее снижение  ).
).
Статические характеристики асинхронного двигателя. Обычно более 50 % нагрузки составляют асинхронные двигатели. На рис. 2.14 показана расчетная схема, где отдельный асинхронный двигатель (АД) подключен к шинам с напряжением  . На рис. 2.15 приведены упрощенные схемы замещения АД.
. На рис. 2.15 приведены упрощенные схемы замещения АД.
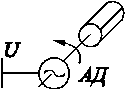 Рис. 2.14. Расчетная
схема АД
Рис. 2.14. Расчетная
схема АД
|  Рис. 2.15. Схемы замещения АД
Рис. 2.15. Схемы замещения АД
|
На схемах замещения рис. 2.15 обозначено:  - индуктивное сопротивление рассеяния цепи статора;
- индуктивное сопротивление рассеяния цепи статора;  - сопротивление ротора, приведенное к статору;
- сопротивление ротора, приведенное к статору;  - активное сопротивление ротора, приведенное к статору;
- активное сопротивление ротора, приведенное к статору;  - сопротивление рассеяния двигателя;
- сопротивление рассеяния двигателя; 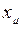 - индуктивное сопротивление намагничивания;
- индуктивное сопротивление намагничивания;  - скольжение:
- скольжение:
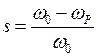 ,
,
где  - частота вращения магнитного поля статора (синхронная частота),
- частота вращения магнитного поля статора (синхронная частота),  - частота вращения ротора двигателя.
- частота вращения ротора двигателя.
Использование схем замещения, приведенных на рис. 2.15, а, б, соответствует неучету электромагнитных переходных процессов, но это допускается при расчетах устойчивости двигателя и позволяет его мощности описывать уравнениями, действительными для установившегося режима.
Изменение скольжения влечет за собой изменение эквивалентного сопротивления двигателя.
Активная мощность, потребляемая асинхронным двигателем из сети (рис. 2.15, б):
 . (2.47)
. (2.47)
При  мощность
мощность 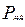 является функцией скольжения
является функцией скольжения  . На рис. 2.16 показаны графики зависимости потребляемой мощности или вращающего момента двигателя от скольжения для постоянных номинального и пониженных значений напряжения на его выводах.
. На рис. 2.16 показаны графики зависимости потребляемой мощности или вращающего момента двигателя от скольжения для постоянных номинального и пониженных значений напряжения на его выводах.

Рис. 2.16. Характеристики двигателя 
|
|
|
при различных постоянных напряжениях
Характеристики мощности  согласно (2.47) изменяются пропорционально квадрату напряжения на выводах. Предполагая момент приводного механизма
согласно (2.47) изменяются пропорционально квадрату напряжения на выводах. Предполагая момент приводного механизма  постоянным (
постоянным ( ), можно установить, что уменьшение напряжения на выводах должно сопровождаться увеличением скольжения до такого значения, чтобы вращающий момент вновь уравновесил бы тормозящий момент - момент приводного механизма (
), можно установить, что уменьшение напряжения на выводах должно сопровождаться увеличением скольжения до такого значения, чтобы вращающий момент вновь уравновесил бы тормозящий момент - момент приводного механизма (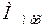 ).
).
При неизменном моменте приводного механизма ( ), регулирующий по активной мощности, очевидно, равен нулю (
), регулирующий по активной мощности, очевидно, равен нулю ( ).
).
Реактивная мощность, потребляемая двигателем  состоит из двух слагаемых:
состоит из двух слагаемых:
 , (2.48)
, (2.48)
где  - мощность намагничивания, зависит от
- мощность намагничивания, зависит от  ;
;  - мощность рассеяния
- мощность рассеяния
 , (2.49)
, (2.49)
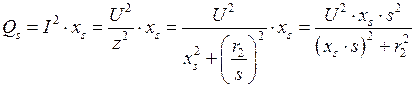 . (2.50)
. (2.50)
Зависимость  представлена на рис. 2.17 и получена с использованием (2.47)-(2.50) в следующем порядке:
представлена на рис. 2.17 и получена с использованием (2.47)-(2.50) в следующем порядке:
1) задаются скольжениями  и по (2.47) при
и по (2.47) при  соответственно находят ряд напряжений;
соответственно находят ряд напряжений;
2) по найденным значениям напряжений по (2.49)-(2.50) определяют составляющие, а по (2.48) - полную мощность.
Изменение активной мощности двигателя при изменении частоты. При неизменном напряжении на выводах двигателя и в предположении, что момент приводного механизма на валу остается постоянным  , активная мощность
, активная мощность 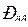 изменяется пропорционально частоте.
изменяется пропорционально частоте.

Рис. 2.17. Зависимость потребляемой реактивной мощности асинхронного
двигателя  от напряжения
от напряжения
Потребляемую двигателем реактивную мощность  при изменении частоты необходимо рассматривать для двух ее составляющих
при изменении частоты необходимо рассматривать для двух ее составляющих  и
и  :
:
 . (2.51)
. (2.51)
График изменения  от частоты представлен на рис. 2.18. Из (2.51) и рис. 2.18 видно, что составляющая
от частоты представлен на рис. 2.18. Из (2.51) и рис. 2.18 видно, что составляющая  уменьшается с уменьшением частоты и растет с ее увеличением, составляющая
уменьшается с уменьшением частоты и растет с ее увеличением, составляющая  напротив возрастает с уменьшением частоты. Соотношение между этими составляющими (рис. 2.18) в обычных асинхронных двигателях таково, что характер изменения результирующей мощности
напротив возрастает с уменьшением частоты. Соотношение между этими составляющими (рис. 2.18) в обычных асинхронных двигателях таково, что характер изменения результирующей мощности  определяется первой слагающей (2.51) при малых снижениях частоты и второй - при значительном ее росте.
определяется первой слагающей (2.51) при малых снижениях частоты и второй - при значительном ее росте.
|
|
|

Рис. 2.18. Изменение мощности, потребляемой двигателем
Статические характеристики синхронных машин (синхронные двигатели, синхронные компенсаторы) определяются аналогично синхронным генераторам.
Статические характеристики комплексной нагрузки. В реальных условиях нагрузка включает все рассматриваемые типы потребителей. В зависимости от процентного состава различных типов потребителей такой комплексной нагрузки ее статические характеристики существенно изменяются.
Выражения изменения активной и реактивной нагрузки  при изменении напряжения узла и частоты в общем виде можно представить следующим образом:
при изменении напряжения узла и частоты в общем виде можно представить следующим образом:

Выражение для 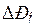 запишем иначе:
запишем иначе:
 .
.
Окончательно получим:
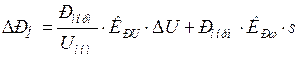 . (2.52)
. (2.52)
После аналогичных преобразований можно получить выражение и для  :
:
 . (2.53)
. (2.53)
В выражениях (2.52), (2.53) регулирующие эффекты для различных составов комплексной нагрузки находятся в пределах
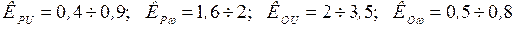 .
.
В настоящее время для различных узлов нагрузки экспериментально получены и продолжают уточняться статистические характеристики, отражающие особенности свойств приемников этих узлов. Вместе с ними практическое применение в расчетах устойчивости находят применение типовые статические характеристики комплексной нагрузки, полученные для усредненной модели системы электроснабжения потребителей от шин 110 и 6(10) кВ районных подстанций. Характеристики представляются в виде таблиц или графиков 
 , приведенных на рис. 2.19.
, приведенных на рис. 2.19.

Рис. 2.19. Статические характеристики комплексной нагрузки
по напряжению (а), по частоте (б)
Значения мощностей, заданных таблично или зависимостями рис. 2.19, как и регулирующие эффекты представлены в относительных единицах и должны быть умножены на действительное значение соответственно активной и реактивной мощности в нормальном режиме. Регулирующие эффекты нагрузок при напряжениях и частоте, отличных от номинальных, могут быть получены по соответствующим кривым.
|
|
|


