Формула полной вероятности

И ФОРМУЛА БЕЙЕСА

Теоретические сведения и примеры решения задач

Вероятность события А, которое может произойти одновременно с одним из n попарно несовместных событий Н ₁, Н ₂,... Н_n, называемых гипотезами, образующих полную группу событий, выражается по формуле полной вероятности:

.

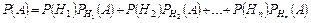После того, как произошло событие А, вероятность события Н_i (i =1, 2,…, n) определяется по формуле Бейеса следующим образом:

.

Задача. В магазин поступила продукция трех фабрик в соотношении 2:5:3. Средний процент нестандартных изделий для продукции первой фабрики равен 3 %, второй – 2 %, третьей – 1 %. Найти вероятность того, что наудачу взятое изделие окажется стандартным. Наудачу

взятое изделие оказалось стандартным. Найти вероятность того, что оно произведено на второй фабрике.

Решение. Обозначим события: А – наудачу взятое изделие окажется стандартным; Н ₁ − взятое изделие произведено на первой фабрике, Н ₂ − взятое изделие произведено на второй фабрике, Н ₃ − взятое изделие произведено на третьей фабрике. В рассматриваемом опыте событие А может произойти с одним из событий Н ₁, Н ₂ или Н ₃. Для решения задачи будет использоваться формула полной вероятности.

По условию задачи

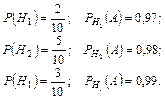
Применяя формулу полной вероятности, получим

Пусть взятое изделие оказалось стандартным. Найдем вероятность того, что оно произведено на второй фабрике. Для этого воспользуемся формулой Бейеса:

 

 

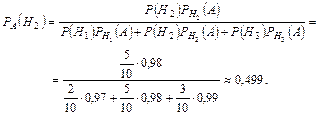
Варианты задачи № 3

1. Охотник сделал три выстрела по кабану. Вероятность попадания первым выстрелом 0,4, вторым – 0,5, третьим – 0,7. Одним попаданием кабана можно убить с вероятностью 0,2, двумя попаданиями – с вероятностью 0,6, а тремя – наверняка. Найти вероятность того, что кабан будет убит.

 

2. В одном из трех ящиков шесть белых и четыре черных шарика, во втором – семь белых и три черных, в третьем – только восемь белых. Наугад выбираем один из трех ящиков и из него снова наугад выбираем один шарик. Он оказался белым. Какова вероятность того, что этот шарик вынут из второго ящика?

 

3. Из 10 студентов, которые пришли на экзамен по математике, трое подготовились отлично, четверо хорошо, двое удовлетворительно, а один совсем не готовился – понадеялся на то, что все помнит. В билетах 20 вопросов. Отлично подготовившиеся студенты могут ответить на все 20 вопросов, хорошо – на 16 вопросов, удовлетворительно – на 10 и не подготовившиеся – на пять вопросов. Каждый студент получает наугад три вопроса из 20. Приглашенный первым студент ответил на все три вопроса. Какова вероятность того, что он отличник?

 

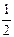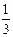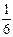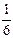4. Путешественник может купить билет в одной из трех касс железнодорожного вокзала. Вероятность того, что он направится к первой кассе, равна , ко второй – , к третьей – . Вероятности того, что билетов уже нет в кассах, такие: в первой кассе , во второй – , в третьей – . Путешественник обратился в одну из касс и получил билет. Определите вероятность того, что он направился к первой кассе.

 

5. В одном из ящиков 10 белых и шесть черных шариков, во втором – семь белых и девять черных. Произвольно выбирается ящик, из него наугад вынимается шарик. Он белый. Чему равна вероятность того, что и второй шарик, наугад вынутый из этого ящика, окажется белым?

 

6. При разрыве снаряда образуются осколки трех весовых категорий: крупные, средние и мелкие, причем число крупных, средних и мелких осколков составляет соответственно 0,1; 0,3; 0,6 общего числа осколков. При попадании в броню крупный осколок пробивает ее с вероятностью 0,9, средний – с вероятностью 0,2 и мелкий – с вероятностью 0,05. В броню попал один осколок и пробил ее. Найдите вероятности того, что эта пробоина причинена крупным, средним и мелким осколком.

 

7. Два зенитных орудия ведут огонь по одному и тому же самолету. Вероятность попадания выстрелом из первого орудия 0,2, из второго – 0,6. Первым залпом в самолет попали только из одного орудия. Какова вероятность того, что промахнулся расчет первого орудия?

 

8. Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут пять дорог. Если турист пойдет по первой дороге, то вероятность выхода туриста из леса в течение часа составляет 0,6; если по второй – 0,3; если по третьей – 0,2; если по четвертой – 0,1; если по пятой – 0,1. Какова вероятность того, что турист пошел по первой дороге, если он через час вышел из леса?

 

9. При помещении в урну перемешанных 10 шаров (шесть белых и четыре черных) один шар неизвестного цвета затерялся. Из оставшихся в урне девяти шаров наудачу вынимают один шар. Какова вероятность того, что вынутый шар окажется белым?

 

10. В цехе работают 20 станков. Из них 10 марки А, шесть марки В и четыре марки С. Вероятности того, что качество детали окажется отличным, для этих станков соответственно равны 0,9; 0,8 и 0,7. Какой процент отличных деталей выпускает цех в целом?

 

11. На рисунке 1 изображена схема дорог. Туристы вышли из пункта О, выбирая наугад на разветвлении дорог один из возможных путей. Какова вероятность того, что они попадут в пункт А?

 

 

Рисунок 1

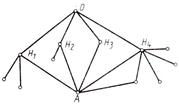
12. Имеются две урны: в первой три белых шара и два черных, во второй четыре белых и четыре черных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.

 

13. Два стрелка независимо друг от друга стреляют по одной
мишени, делая каждый по одному выстрелу. Вероятность попадания в

мишень для первого стрелка 0,8, для второго 0,4. После стрельбы
в мишени обнаружена одна пробоина. Найти вероятность того, что
в мишень попал первый стрелок.

 

14. На фабрике, изготовляющей болты, первая машина производит 25 %, вторая – 35 %, третья – 40 % всех изделий. В их продукции брак составляет соответственно 5, 4 и 2 %. Какова вероятность того, что:

а) случайно выбранный болт будет дефектный;

б) дефектный болт был произведен первой, второй, третьей машиной?

 

15. Детали для сборки вырабатываются на двух станках, из которых первый производит в три раза больше второго. При этом брак составляет в выпуске первого станка 0,025, а в выпуске второго – 0,015. Одна, взятая наудачу деталь, оказалась годной для сборки. Найти вероятность того, что она изготовлена на втором станке.

 

16. 30 % приборов собирает специалист высокой квалификации и 70 % − специалист средней квалификации. Надежность работы прибора, собранного специалистом высокой квалификации, 0,9, надежность прибора, собранного специалистом средней квалификации, 0,8. Взятый прибор оказался надежным. Определить вероятность того, что он собран специалистом высокой квалификации.

 

17. Имеются две партии изделий по 12 и 10 штук, причем в каждой партии одно изделие бракованное. Изделие, взятое наудачу из первой партии, переложено во вторую, после чего выбирается наудачу изделие из второй партии. Определить вероятность извлечения бракованного изделия из второй партии.

 

18. Известно, что 96 % выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает деталь годной для стандартной продукции с вероятностью 0,98 и нестандартной – с вероятностью 0,05. Определить вероятность того, что изделие, прошедшее упрощенный контроль, удовлетворяет стандарту.

 

19. Из 18 стрелков пять попадают в мишень с вероятностью 0,8; семь – с вероятностью 0,7; четыре – с вероятностью 0,6 и два – с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок?

 

20. Трое охотников одновременно выстрелили по вепрю, который был убит одной пулей. Определить вероятности того, что вепрь убит первым, вторым или третьим охотником, если вероятности попадания для них равны соответственно 0,2; 0,4; 0,6.

 

21. Попадание случайной точки в любое место области S равновозможно, а область S состоит из четырех частей, составляющих соответственно 50, 30, 12 и 8 % всей области. При испытании имело место событие А, которое происходит только при попадании случайной точки в одну из этих частей с вероятностями соответственно 0,01; 0,05; 0,2; 0,5. В какую из частей области S вероятнее всего произошло попадание?

 

22. Электролампы изготавливаются на трех заводах. Первый завод производит 45 % общего количества электроламп, второй – 40 %, третий – 15 %. Продукция первого завода содержит 70 % стандартных ламп, второго – 80 %, третьего – 81 %. В магазины поступает продукция всех трех заводов. Какова вероятность того, что купленная в магазине лампа окажется стандартной?

 

23. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,3 % брака, второй – 0,2 % и третий – 0,4 %. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000, со второго – 2000 и с третьего – 2500 деталей.

 

24. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше, чем второго, а третьего в два раза меньше, чем второго. Определить вероятность того, что взятая наудачу деталь будет бракованной.

 

25. По самолету производится три одиночных выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором – 0,6, при третьем – 0,8. Для вывода самолета из строя заведомо достаточно трех попаданий: при одном попадании самолет выходит из строя с вероятностью 0,3, при двух попаданиях – с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет сбит.

 

26. В трех урнах находятся белые и черные шары: в первой – два белых и три черных, во второй – два белых и два черных, в третьей –

три белых и один черный. Из первой урны переложили шар во вторую. После этого шар из второй урны переложили в третью. Наконец, из третьей урны его переложили в первую. Чему равна вероятность того, что состав шаров во всех урнах не изменится?

 

27. Литье в болванках поступает из двух заготовительных цехов: 70 % из первого и 30 % из второго. При этом материал первого цеха имеет 10% брака, а второго – 20 %. Найти вероятность того, что одна взятая наугад болванка без дефектов.

 

28. Имеется 12 урн, из них в шести урнах (состав А1) по три белых и четыре черных шара, в трех урнах (состав А2) по два белых и восемь черных шаров, в двух урнах (состав А3) по шесть белых и одному черному шару, в одной урне (состав А4) четыре белых и три черных шара. Из наугад выбранной урны взят один шар. Чему равна вероятность того, что шар взят из урны состава А3, если он оказался белым?

 

29. На склад поступает продукция трех фабрик. Причем продукция первой фабрики составляет 20 %, второй – 46 %, третьей – 34 %. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3 %, для второй – 2 % и, наконец, для третьей – 1 %. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось нестандартным.

 

30. Имеется 10 одинаковых по виду урн, из которых в девяти находится по два черных и два белых шара, а в одной – пять белых и один черный шар. Из наугад взятой урны извлечен шар. Чему равна вероятность того, что этот шар извлечен из урны, содержащей пять белых шаров, если он оказался белым?

 

3.3 Теоретические вопросы к защите расчетного задания № 3

 

1. Что называют гипотезами?

2. Какому условию должны удовлетворять вероятности гипотез?

3. Как выглядит формула полной вероятности?

4. При каком условии применяется формула полной вероятности?

5. Как выглядит формула Бейеса?

6. При каких условиях применяется формула Бейеса?

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: