 |
Теоретические сведения и примеры решения задач
|
|
|
|
Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.
Нулевой гипотезой Н0 называется проверяемая гипотеза.
Вероятность допустить ошибку, а именно: отвергнуть верную гипотезу Н0, называется уровнем значимости.
Правило, по которому нулевая гипотеза отвергается или принимается, называется статистическим критерием.
Статистический критерий, служащий для проверки гипотез о виде закона распределения, называется критерием согласия.
Критерий согласия Пирсона  :
:
 ,
,
где  - эмпирические частоты случайной величины Х;
- эмпирические частоты случайной величины Х;
 - теоретические частоты;
- теоретические частоты;
 - вероятности, рассчитанные по предполагаемому теоретическому распределению.
- вероятности, рассчитанные по предполагаемому теоретическому распределению.
Схема применения критерия согласия Пирсона  сводится к следующему:
сводится к следующему:
а) определяется мера расхождения теоретических и эмпирических частот, вычисляется статистика  ;
;
б) для выбранного уровня значимости 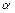 по таблице распределения
по таблице распределения  (таблица А4 Приложения А) находится критическое значение
(таблица А4 Приложения А) находится критическое значение  при числе степеней свободы
при числе степеней свободы  , где m – число выборочных
, где m – число выборочных
групп, s - число параметров теоретического распределения, определяемого по опытным данным.
в) если наблюдаемое значение  больше критического, то гипотеза Н0 отвергается, в противном случае гипотеза не противоречит опытным данным на заданном уровне значимости.
больше критического, то гипотеза Н0 отвергается, в противном случае гипотеза не противоречит опытным данным на заданном уровне значимости.
При использовании критерия Пирсона следует помнить, что он дает удовлетворительные результаты, если в каждом группировочном интервале число наблюдений не меньше 5. В противном случае имеет смысл объединить соседние интервалы. При этом соответствующим образом уменьшится число степеней свободы.
Задача. Получено следующее распределение 100 рабочих цеха по выработке в отчетном году (в % к предыдущему году):
|
|
|
| Выработка в отчетном году (в % к предыдущему году) | Менее 104 | 104-114 | 114-124 | 124-134 | Более 134 |
| Количество рабочих |
С помощью критерия согласия Пирсона  проверить гипотезу о том, что выработка на одного рабочего в отчетном году (в % к предыдущему) подчиняется нормальному закону распределения. Уровень значимости критерия принять равным 0,05.
проверить гипотезу о том, что выработка на одного рабочего в отчетном году (в % к предыдущему) подчиняется нормальному закону распределения. Уровень значимости критерия принять равным 0,05.
Решение. Нулевая гипотеза Н0 состоит в том, что исследуемый признак Х – выработка на одного рабочего в отчетном году (в % к предыдущему) подчиняется нормальному закону распределения.
В качестве оценок двух неизвестных параметров а и  будут фигурировать соответствующие выборочные характеристики:
будут фигурировать соответствующие выборочные характеристики:  и
и  . Можно показать, что
. Можно показать, что 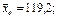
 . Исследуемый признак принимает значения на всей вещественной оси (в принципе, но не в реальности). Поэтому интервалы разбиения таковы, что левый конец
. Исследуемый признак принимает значения на всей вещественной оси (в принципе, но не в реальности). Поэтому интервалы разбиения таковы, что левый конец 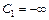 и правый конец
и правый конец  .
.
Теоретические вероятности  находятся по формуле
находятся по формуле
 , i = 1, 2, …, k.
, i = 1, 2, …, k.
Необходимые для этих вычислений значения функции  взяты из таблицы А1 Приложения А. Дальнейшие выкладки сведены ниже в таблицу. При этом объединены два последних интервала группировки ввиду их малочисленности.
взяты из таблицы А1 Приложения А. Дальнейшие выкладки сведены ниже в таблицу. При этом объединены два последних интервала группировки ввиду их малочисленности.
| Интервал группи-ровки | Частота 
| 
| Функция 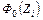
| Вероят-ность 
| 
| 
|

| −∞ | −0,5 | 0,053 | 5,3 | 0,092 | |
| −1,62 | −0,447 | 0,238 | 23,8 | 0,636 | |

| −0,55 | −0,209 | 0,404 | 40,4 | 0,524 | |

| 0,51 | 0,195 | 0,248 | 24,8 | 0,026 | |

| 1,57 | 0,442 | 0,057 | 5,7 | 0,11 | |
| − | − | + ∞ | 0,5 | − | − | − |

| 
|
Вычисленное статистическое значение критерия  .
.
По количеству интервалов группировки m = 5, числу параметров
нормального распределения  найдем число степеней свободы
найдем число степеней свободы
5 – 3 = 2. Для заданного уровня значимости критерия  и числа степеней свободы k = 2 по таблице А4 Приложения А находим
и числа степеней свободы k = 2 по таблице А4 Приложения А находим  . Так как
. Так как 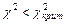 , то нулевая гипотеза о нормальном распределении величины выработки рабочего согласуется
, то нулевая гипотеза о нормальном распределении величины выработки рабочего согласуется
с имеющимися данными.
|
|
|
Варианты задачи № 10
Используя критерий согласия Пирсона при уровне значимости a=0,05, необходимо:
а) проверить, что случайная величина X распределена по нормальному закону;
б) построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
1. Из 1800 изготовленных приборов было отобрано 200. Получено распределение по продолжительности работы
| Продолжительность работы прибора | 33-34 | 34-35 | 35-36 | 36-37 | 37-38 | Всего |
| Количество приборов |
2. Из 100 предприятий отрасли проверено 100. Получено распределение предприятий по проценту выполнения плана по сравнению с предыдущим годом
| Выполнение плана X | 85-90 | 90-95 | 95-100 | 100-105 | 105-110 | Всего |
| Количество предприятий |
3. Автомат наполняет ампулы лекарственным раствором. Контрольная проверка 100 ампул дала распределение в них лекарства
| Объем лекарств в ампуле X, см3 | Менее 1,9 | 1,9-1,94 | 1,94-1,98 | 1,98-2,02 | 2,02-2,06 | 2,06-2,1 | Всего |
| Число ампул |
4. Некоторой французской кинокомпанией выпущено 800 фильмов. Отобрано 100 фильмов. Распределение их по времени демонстрации фильма (в минутах) представлено в таблице
| Время демонстрации фильма X, мин | До 30 | 30-60 | 60-90 | 90-120 | 120-150 | 150-180 | Всего |
| Количество фильмов |
5. Из поступающих в цех заготовок по схеме собственно случайной бесповторной выборки было отобрано для взвешивания 200 штук. Получено распределение заготовок по их массе
| Масса заготовок X, г | 73-75,5 | 75,5-78 | 78-80,5 | 80,5-83 | 83-85,5 | 85,5-88 | 88-90,5 | 90,5-93 | Всего |
| Число наблюдений |
6. Из 200 спортсменов-лыжников по схеме собственно случайной бесповторной выборки отобрано 80 лыжников. По результатам обследования их по времени восстановления пульса после прохождения дистанции получены следующие данные:
| Время восстановления пульса после прохождения дистанции, с | 72-76 | 76-80 | 80-84 | 84-88 | 88-92 | Всего |
| Число лыжников |
7. Для контроля массы упаковки (пакетов) из партии 50000 ед. проверили 1000 пакетов, в результате получены данные
|
|
|
| Масса пакета, г | 900-940 | 940-980 | 980-1020 | 1020-1060 | 1060-1100 | 1100-1140 | Всего |
| Число пакетов |
8. Из стада в 5000 овец было отобрано 200 овец для контрольной проверки массы настриженной шерсти. Получены следующие данные:
| Настриг шерсти с одной овцы, кг | 2,8-3,7 | 3,7-4,6 | 4,6-5,5 | 5,5-6,4 | 6,4-7,3 | 7,3-8,2 | Всего |
| Число овец |
9. Проведены испытания чувствительности второго канала у телевизоров одной марки из 200 таких телевизоров. Получены следующие результаты:
| Чувствительность второго канала | 40-140 | 140-240 | 240-340 | 340-440 | 440-540 | 540-640 | Всего |
| Число телевизоров |
10. Из 10000 абонементов библиотеки было отобрано 200 для изучения количества книг, взятых читателями за год, и получены следующие результаты:
| Количество взятых за год книг, шт. | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | Всего |
| Число абонементов |
11. Результаты исследования числа покупателей в универсаме в зависимости от времени работы приведены в таблице
| Часы работы | 9-10 | 10-11 | 11-12 | 12-13 |
| Число покупателей |
12. Масса (в граммах) произвольно выбранных 30 пачек полуфабриката «Геркулес» такова:
| Масса, г | 485-491 | 491-497 | 497-503 | 503-509 | 509-515 |
| Количество пачек |
13. Из 1000 жителей региона месячный доход жителей региона в руб. представлен в таблице
| Месячный доход | Менее 500 | 500-1000 | 1000-1500 | 1500-2000 | 2000-2500 | Свыше 2500 |
| Количество жителей |
14. Удой коров на молочной ферме (в ц) среди 100 обследованных коров представлен в таблице
| Удой, ц | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 | 20-22 | 22-24 | 24-26 |
| Количество коров |
15. Из большой партии было проверено 150 изделий с целью определения процента влажности древесины, из которой изготовлены эти изделия. Получены результаты
| Процент влажности | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 |
| Число изделий |
16. Распределение 100 рабочих цеха по выработке в отчетном году (в процентах к предыдущему) представлено в таблице
|
|
|
| Выработка в отчетном году | 90-104 | 104-114 | 114-124 | 124-134 | 134-144 |
| Количество рабочих |
17. Распределение числового признака X в выборке определяется таблицей
| X | 3,0-3,6 | 3,6-4,2 | 4,2-4,8 | 4,8-5,4 | 5,4-6,0 | 6,0-6,6 | 6,6-7,2 |
| ni |
18. Даны значения пористости напыленного покрытия шейки распределительного вала автомобиля
| Пористость, % | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 |
| Количество валов |
19. Результаты измерений диаметров 80 отверстий одним и тем же сверлом (в мм)
| Диаметр | 40,24-40,28 | 40,28-40,32 | 40,32-40,36 | 40,36-40,4 | 40,4-40,44 |
| Количество отверстий |
20. Даны значения внутреннего диаметра гайки (в мм)
| Внутренний диаметр гайки | 4,00-4,20 | 4,20-4,40 | 4,40-4,60 | 4,60-4,80 | 4,80-5,00 |
| Количество гаек |
21. Отклонения диаметров валиков, обработанных на станке, от заданного размера (в мкм) представлены в таблице
| Отклонение диаметров валиков | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| Количество валиков |
22. Дана трудоемкость операции «смазка подшипников подвески автомобиля БеЛАЗ» (в с)
| Трудоемкость, с | 30-35 | 35-40 | 40-45 | 45-50 | 50-55 |
| Количество операций |
23. Сведения о расходе воды, используемой заводом для технических нужд, в течение 100 дней (в куб. м)
| Расход воды, м3 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 |
| Количество дней |
24. Даны результаты наблюдений за сроком службы 100 однотипных станков до выхода за пределы норм точности (в месяцах двухсменной работы)
| Срок службы станка, мес | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 |
| Количество станков |
25. Даны квартальные данные о среднесуточном пробеге 60 автомобилей (в км)
| Среднесуточный пробег автомобилей, км | 150-170 | 170-190 | 190-210 | 210-230 | 230-250 |
| Количество автомобилей |
26. Даны размеры 200 деталей после шлифовки (в мм)
| Размер детали после шлифовки | 3,45-3,65 | 3,65-3,85 | 3,85-4,05 | 4,05-4,25 | 4,25-4,45 |
| Количество деталей |
27. Даны результаты испытания стойкости (в часах) 100 фрез
| Стойкость фрез, ч | 22,5-27,5 | 27,5-32,5 | 32,5-37,5 | 37,5-42,5 | 42,5-47,5 |
| Количество фрез |
28. Даны результаты измерения толщины 50 слюдяных прокладок (в см)
| Толщина слюдяных прокладок, см | 0,24-0,28 | 0,28-0,32 | 0,32-0,36 | 0,36-0,40 | 0,40-0,44 |
| Количество прокладок |
29. Даны результаты определения содержания фосфора (в %) в 100 чугунных образцах
| Содержание фосфора в чугуне, % | 0,10-0,20 | 0,20-0,30 | 0,30-0,40 | 0,40-0,50 | 0,50-0,60 |
| Количество образцов |
30. Систематические данные о трудоемкости (в мин) операции «ремонт валика водяного насоса автомобиля» приведены в таблице
|
|
|
| Трудоемкость операции, мин | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Количество валиков |
10.3 Теоретические вопросы к защите расчетного задания № 10
1. Сформулируйте определение понятия статистическая гипотеза.
2. Какие выводы делаются при проверке статистических гипотез?
3. Какую гипотезу называют: а) нулевой; б) конкурирующей;
в) параметрической; г) простой; д) сложной?
4. Определите понятие ошибок первого рода и второго рода.
5. Можно ли одновременно уменьшить вероятности ошибок первого и второго рода?
6. Что называется статистическим критерием?
7. Что называется критической областью?
8. Что называется областью принятия гипотезы?
9. Дайте определение: а) правосторонней критической области;
б) левосторонней критической области; в) двусторонней критической области.
10. Как определяются критические точки: а) правосторонней критической области; б) левосторонней критической области; в) двусторонней критической области?
11. В чем состоит схема проверки статистических гипотез?
12. Что называется критерием согласия?
13. Сформулируйте схему применения критерия согласия «хи-квадрат» Пирсона.
Литература
1. Гмурман, В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. – М.: Высшая школа, 2002.
2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике / В.Е. Гмурман. – М.: Высшая школа, 2002.
3. Вентцель, Е.С. Теория вероятностей / Е.С. Вентцель. – М.: Наука, 1999.
4. Вентцель, Е.С. Задачи и упражнения по теории вероятностей / Е.С. Вентцель, Л.А. Овчаров. – М.: Высшая школа, 2002.
5. Кремер, Н. Ш. Теория вероятностей и математическая статистика: учебник для ВТУЗов / Н.Ш. Кремер. – М.: Юнити, 2001.
6. Ивашев-Мусатов, О.С. Теория вероятностей и математическая статистика / О.С. Ивашев-Мусатов. - М.: Наука, 1979.
7. Гусак, А.А. Теория вероятностей: справочное пособие к решению задач / А.А. Гусак, Е.А. Бричкова. – 2-е изд., стер. – М.: ТетраСистемс, 2000.
ПРИЛОЖЕНИЕ А
Таблицы
Таблица А.1 – Значения функций  и
и 
| х | 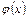
| 
| х | 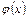
| 
| х | 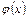
| 
|
| 0,00 | 0,3989 | 0,0000 | 0,30 | 0,3814 | 0,1179 | 0,60 | 0,3332 | 0,2257 |
| 0,10 | 0,3970 | 0,0398 | 0,40 | 0,3683 | 0,1554 | 0,70 | 0,3123 | 0,2580 |
| 0,20 | 0,3910 | 0,0793 | 0,50 | 0,3521 | 0,1915 | 0,80 | 0,2897 | 0,2881 |
Продолжение таблицы А.1
| х | 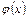
| 
| х | 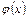
| 
| х | 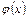
| 
|
| 0,90 | 0,2661 | 0.3159 | 1,30 | 0,1714 | 0,4032 | 1,70 | 0,0940 | 0,4554 |
| 1,00 | 0,2420 | 0,3413 | 1,40 | 0,1497 | 0,4192 | 1,80 | 0,0790 | 0,4641 |
| 1,10 | 0,2179 | 0,3643 | 1,50 | 0,1295 | 0,4332 | 1,90 | 0,0656 | 0,4713 |
| 1,20 | 0,1942 | 0,3849 | 1,60 | 0,1109 | 0,4452 | 2,00 | 0,0540 | 0,4772 |
Продолжение таблицы А.1
| х | 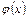
| 
| х | 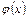
| 
| х | 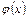
| 
|
| 2,10 | 0,0440 | 0,4821 | 2,46 | 0,0167 | 0,4941 | 2,82 | 0,0071 | 0,4976 |
| 2,50 | 0,0175 | |||||||
| 2,90 | 0,0060 | 0,4981 | ||||||
| 2,20 | 0,0355 | 0,4861 | ||||||
| 2,60 | 0,0136 | 0,4953 | ||||||
| 3,00 | 0,00443 | 0,49865 | ||||||
| 2,30 | 0,0283 | 0,4893 | 3,10 | 0,00327 | 0,49903 | |||
| 3,20 | 0,00238 | 0,49931 | ||||||
| 2,70 | 0,0104 | 0,4965 | 3,40 | 0,00123 | 0,49966 | |||
| 3,60 | 0,00061 | 0,49984 | ||||||
| 3,80 | 0,00029 | 0,49992 | ||||||
| 2,40 | 0,0224 | 0,4918 | 4,00 | 0,00013 | 0,49996 | |||
| 4,50 | 0,00002 | 0,49999 | ||||||
| 2,80 | 0,0079 | 0,4974 | 5,00 | 0,000001 | 0,49999 |
Таблица А.2 – Значения 
| n | 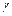
| n | 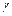
| ||||
| 0,95 | 0,99 | 0,999 | 0,95 | 0,99 | 0,999 | ||
| 2,78 | 4,60 | 8,61 | 2,093 | 2,861 | 3,883 | ||
| 2,57 | 4,03 | 6,86 | 2,064 | 2,797 | 3,745 | ||
| 2,45 | 3,71 | 5,96 | 2,045 | 2,756 | 3,659 | ||
| 2,37 | 3,50 | 5,41 | 2,032 | 2,720 | 3,600 | ||
| 2,31 | 3,36 | 5,-4 | 2,023 | 2,708 | 3,558 | ||
| 2,26 | 3,25 | 4,78 | 2,016 | 2,692 | 3,527 | ||
| 2,23 | 3,17 | 4,59 | 2,009 | 2,679 | 3,502 | ||
| 2,20 | 3,11 | 4,44 | 2,001 | 2,662 | 3,464 | ||
| 2,18 | 3,06 | 4,32 | 1,996 | 2,649 | 3,439 | ||
| 2,16 | 3,01 | 4,22 | 1,991 | 2,640 | 3,418 | ||
| 2,15 | 2,98 | 4,14 | 1,987 | 2,633 | 3,403 | ||
| 2,13 | 2,95 | 4,07 | 1,984 | 2,627 | 3,392 | ||
| 2,12 | 2,92 | 4,02 | 1,980 | 2,617 | 3,374 | ||
| 2,11 | 2,90 | 3,97 | ∞ | 1,960 | 2,576 | 3,291 | |
| 2,10 | 2,88 | 3,92 |
Таблица А.3 – Критические точки распределения Стьюдента
| Число степеней свободы k | Уровень значимости 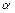
| |||||
| 0,1 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 6,31 | 12,7 | 31,82 | 63,7 | 318,3 | 637,0 | |
| 2,92 | 4,3 | 6,97 | 9,92 | 22,33 | 31,6 | |
| 2,35 | 3,18 | 4,54 | 5,84 | 10,22 | 12,9 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 2,01 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 | |
| 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 1,89 | 2,36 | 3,00 | 3,50 | 4,79 | 5,40 | |
| 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 | |
| 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 | |
| 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 | |
| 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,01 | |
| 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,96 | |
| 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 | |
| 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 | |
| 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 | |
| 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 | |
| 1,72 | 2,07 | 2,51 | 2,82 | 3,51 | 3,79 | |
| 1,71 | 2,07 | 2,50 | 2,81 | 3,49 | 3,77 | |
| 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,74 | |
| 1,71 | 2,06 | 2,49 | 2,79 | 3,45 | 3,72 | |
| 1,71 | 2,06 | 2,48 | 2,78 | 3,44 | 3,71 | |
| 1,71 | 2,05 | 2,47 | 2,77 | 3,42 | 3,69 | |
| 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 | |
| 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 | |
| 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 | |
| 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 | |
| 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 | |
| 1,66 | 1,98 | 2,36 | 2,62 | 3,17 | 3,37 | |
| ∞ | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
Таблица А.4 – Критические точки распределения 
| Число степеней свободы k | Уровень значимости 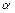
| |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 6,6 | 5,0 | 3,8 | 0,0039 | 0,00098 | 0,00016 | |
| 9,2 | 7,4 | 6,0 | 0,103 | 0,051 | 0,020 | |
| 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 | |
| 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 | |
| 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 | |
| 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 | |
| 18,5 | 16,0 | 14,1 | 2,17 | 1,69 | 1,24 | |
| 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 | |
| 21,7 | 19,0 | 16,9 | 3,33 | 2,70 | 2,09 | |
| 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 | |
| 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 | |
| 26,2 | 23,3 | 21,0 | 5,23 | 4,40 | 3,57 | |
| 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 | |
| 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 | |
| 30,6 | 27,5 | 25,0 | 7,26 | 6,26 | 5,23 | |
| 32,0 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 | |
| 34,8 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 | |
| 33,4 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 | |
| 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 | |
| 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 | |
| 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,90 | |
| 40,3 | 36,8 | 33,9 | 12,3 | 11,0 | 9,54 | |
| 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 | |
| 43,0 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 | |
| 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 | |
| 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 | |
| 47,0 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 | |
| 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 | |
| 49,6 | 45,7 | 42,6 | 17,7 | 16,0 | 14,3 | |
| 50,9 | 47,0 | 43,8 | 18,5 | 16,8 | 15,0 |
СОДЕРЖАНИЕ
ТРЕБОВАНИЯ К ПРЕДСТАВЛЕНИЮ И ОФОРМЛЕНИЮ РЕЗУЛЬТАТОВ ТИПОВОГО РАСЧЕТА 3
1 КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.. 3
2 ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ.. 9
3 ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ.. 15
И ФОРМУЛА БЕЙЕСА.. 15
4 СХЕМА ПОВТОРНЫХ НЕЗАВИСИМЫХ ИСПЫТАНИЙ.. 22
5 ДИСКРЕТНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 28
6 НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ... 35
7 СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН.. 51
8 ИНТЕРВАЛЬНАЯ ОЦЕНКА ПАРАМЕТРОВ
РАСПРЕДЕЛЕНИЯ.. 57
9 ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ.. 57
10 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ... 57
Литература……………………………………………………………… 92
ПРИЛОЖЕНИЕ А. Таблицы. 57
КУВШИНОВА Лидия Павловна
ТУШКИНА Татьяна Михайловна
ШАЙХУДИНОВА Татьяна Алексеевна
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические рекомендации и контрольные задания к типовому расчету для студентов специальностей 230201, 080801, 200106, 080502, 080301, 190603, 170104, 160302, 151001, 260204, 260601, 080401, 220501, 240706, 240901, 240701, 240702, 080109
Редактор Идт Л.И.
Технический редактор Малыгина Ю.Н.
Корректор Малыгина И.В.
Подписано в печать 25.10.07. Формат 60х84 1/16.
Усл. п. л. 5,75. Уч.-изд. л. 6,19.
Печать – ризография, множительно-копировальный
аппарат «RISO TR -1510»
Тираж 100 экз. Заказ 2007-61.
Издательство Алтайского государственного
технического университета,
656038, г. Барнаул, пр-т Ленина, 46
Оригинал-макет подготовлен ИИО БТИ АлтГТУ.
Отпечатано в ИИО БТИ АлтГТУ.
659305, г. Бийск, ул. Трофимова, 29
|
Л.П. Кувшинова, Т.М. Тушкина, Т.А. Шайхудинова
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
|
|
|



